ডাইনামিক প্রোগ্রামিং নামটা শুনতে একটু কঠিন মনে হলেও এর পিছনে কনসেপ্টটা বেশ সহজ। ডাইনামিক প্রোগ্রামিং কে এক কথায় বর্ণনা করতে গেলে বলা যায় – একটা সমস্যাকে ছোট ছোট ভাগ করে সাব-প্রবলেমগুলো সমাধান করবো তবে একই সাবপ্রবলেম একবারের বেশি সমাধান করবো না। মোটা দাগে বলতে গেলে এটাই ডাইনামিক প্রোগ্রামিং। তবে কখন একটা প্রবলেমকে ডাইনামিক প্রোগ্রামিং দিয়ে সমাধান করা যাবে সেটা বুঝতে একটু অভিজ্ঞতা প্রয়োজন। তো এই সিরিজে আমরা দেখবো ডাইনামিক প্রোগ্রামিং কি এবং কিছু কমন সমস্যা যেগুলো ডাইনামিক প্রোগ্রামিং দিয়ে সমাধান করা যায়।
ডাইনামিক প্রোগ্রামিং বা ডিপি টার্মটা একটু কনফিউজিং কারণ ‘ডাইনামিক’ শব্দটা এখানে খুব একটা অর্থপূর্ণ উপায়ে ব্যবহার করা হয় নি। কিছু বুরোক্রেটিক কারণে ডক্টর রিচার্ড বেলম্যান (বেলম্যান অ্যালগরিদমের জনক) এই নামটি ব্যবহার করেন, সে গল্পটি তুমি উইকিপিডিয়ায় সার্চ করলে পাবে। একথাটা শুরুতে বলে নেয়ার কারণ হলো আমি জানি ডায়নামিক প্রোগ্রামিং শেখার পর তুমি চিন্তা করবে এই টেকনিকের কোন অংশটা ‘ডাইনামিক’! এটা নিয়ে চিন্তা করার দরকার নেই, রিসার্চ গ্র্যান্ট বাচাতে বেলম্যান এই অদ্ভুত নামটা ব্যবহার করেছেন।
ডাইনামিক প্রোগ্রামিং শেখার প্রথম পূর্বশর্ত হলো রিকার্শন বোঝা। রিকার্শন নিয়ে ভালো ধারণা না থাকলে এই লেখাটা পড়তে পারো। এছাড়াও আশা করবো তোমার টাইম এবং স্পেস কমপ্লেক্সিটি নিয়ে ধারণা আছে।
এই সিরিজের মূল রেফারেন্স হিসাবে ব্যবহার করেছি MIT’র লেকচার সিরিজ, তুমি চাইলে সরাসরি সেখান থেকেই ডিপি শিখে ফেলতে পারো।
ডাইনামিক প্রোগ্রামিং
ডাইনামিক প্রোগ্রামিং একটা নির্দিষ্ট কোন সমস্যা সমাধানের অ্যালগরিদম না, বরং এটা একটা প্রবলেম সলভিং টেকনিক যেটা দিয়ে অনেক ধরণের অপটিমাইজেশন প্রবলেম বা কাউন্টং প্রবলেম সলভ করা যায়, যেমন ফিবোনাচ্চি, কয়েন চেঞ্জ, ম্যাট্রিক্স চেইন মাল্টিপ্লিকেশন। ডাইনামিক প্রোগ্রামিং কে এক ধরণের ব্রুট ফোর্স অ্যালগরিদম বললে ভুল হবে না। এটা একটা প্রবলেমকে ছোট ছোট ভাগে ভাগ করে সব রকম সম্ভাব্য সাবপ্রবলেম থেকে সঠিক সমাধান খুজে নিয়ে আসে। তবে এটা একটু বুদ্ধিমান ব্রুট ফোর্স যা পলিনমিয়াল কমপ্লেক্সিটিতেই কাজ করে। অনেক প্রবলেম আছে যেগুলা সলভ করার একমাত্র পলিনমিয়াল অ্যালগরিদম ডাইনামিক প্রোগ্রামিং।
ফিবোনাচ্চি সিকুয়েন্স
সবথেকে সহজ উদাহরণ দিয়ে আমরা শুরু করবো। ইটালিয়ান গণিতবিদ Leonardo Pisano Bigollo যাকে আমরা ফিবোনাচ্চি নামে চিনি খরগোশের বংশবৃদ্ধি পর্যবেক্ষণ করতে গিয়ে একটা নাম্বার সিরিজ আবিষ্কার করে বসলেন। সিরিজটি এরকম:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34 ….
লক্ষ্য করো ১ম দুটি সংখ্যা ছাড়া প্রতিটি সংখ্যা হলো আগের দুটি সংখ্যার যোগফল। আমরা একটি ফাংশন কল্পনা করি $ যা $ তম ফিবোনাচ্চি সংখ্যা রিটার্ন করে। ফিবোনাচ্চি সংখ্যার ফর্মূলা রিকার্সিভ ফাংশনের মাধ্যমে প্রকাশ করলে আমরা পাবো:
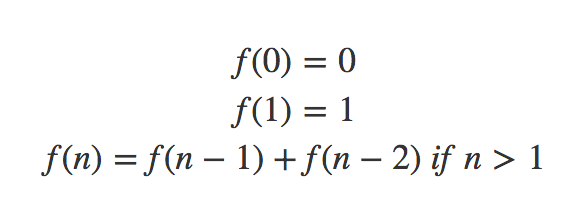সি++ এ কোড লিখলে সেটা হবে এরকম:
|
1 2 3 4 5 6 |
int f(int n) { if (n == 0) return 0; if (n == 1) return 1; return f(n - 1) + f(n - 2); } |
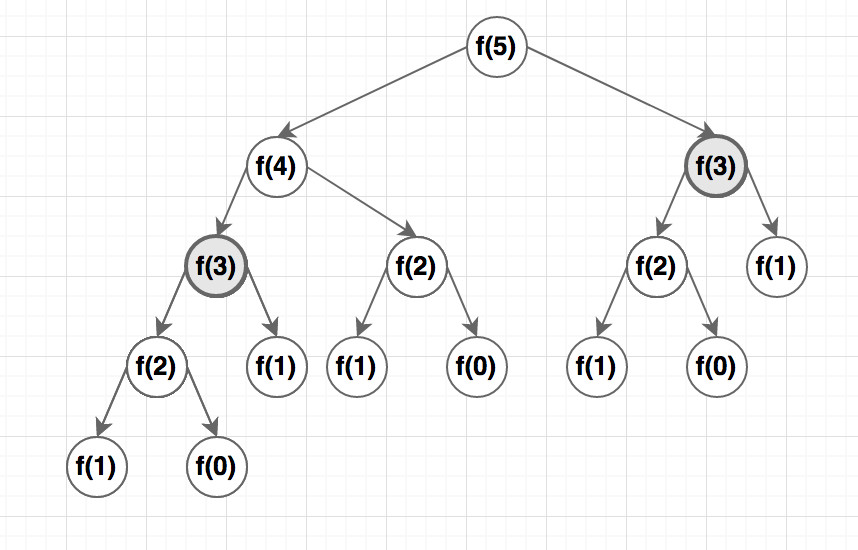
আমরা $f(n)$ প্রবলেমটাকে ছোট দুটো সাবপ্রবলেমে ভাগ করে ফেলতে পেরেছি। এই কোডের কমপ্লেক্সিটি কত সেটাকি তুমি জানো? আমরা যদি ফাংশনটাকে $n = 5$ দিয়ে কল করি তাহলে $5^{th}$ ফিবোনাচ্চি খুজে পেতে কোন কোন ফাংশন কল হবে সেটা নিচের ছবির ট্রি-তে দেখানো হয়েছে:
$0$ থেকে $n$ পর্যন্ত সবগুলো মানের জন্য দুটো করে ফাংশন কল হচ্ছে (বেস কেস ছাড়া)। টাইম কমপ্লেক্সিটি গিয়ে দাড়াচ্ছে $O(2^n)$ এ। এটা এক্সপোনেশিয়াল কমপ্লেক্সিটি যা খুব ধীরগতিতে কাজ করবে। আমাদের আরেকটু ভালো কিছু দরকার।
হয়তো তুমি এরই মধ্যে লক্ষ্য করেছো আমি $f(3)$ কে দুই জায়গায় আলাদা করে চিহ্নিত করে দিয়েছি। $f(5)$ ক্যালকুলেট করতে গিয়ে $f(3)$ কল করা হচ্ছে দুইবার এবং দুইবারই আমরা $f(3)$ এর নিচের সবগুলো সাবপ্রবলেম নতুন করে সলভ করছি।
আমি শুরুতেই ডাইনামিক প্রোগ্রামিং নিয়ে বলেছি ” একটা সমস্যাকে ছোট ছোট ভাগ করে সাব-প্রবলেমগুলো সমাধান করবো তবে একই সাবপ্রবলেম একবারের বেশি সমাধান করবো না”। এখানে আমরা সাবপ্রবলেমে ঠিকই ভাগ করেছি কিন্তু একই সাবপ্রবলেম বারবার সলভ করছি। তো সেটা না করে সাবপ্রবলেমের রেজাল্টগুলো একটা টেবিলে সেভ করে রাখলেই কিন্তু কাজ হয়ে যায়। যদি দেখি যে কোনো সাবপ্রবলেমের রেজাল্ট আমরা জানি তাহলে সেটা আবার সমাধান করার দরকার নেই।
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
#define MAX_N 20 #define EMPTY_VALUE -1 int memo[MAX_N + 1]; int f(int n) { if (n == 0) return 0; if (n == 1) return 1; if (memo[n] != -1) { return memo[n]; } memo[n] = f(n - 1) + f(n - 2); return memo[n]; } void init() { for (int i = 0; i <= MAX_N; i++) { memo[i] = EMPTY_VALUE; } } |
আমরা memo নামের একটা অ্যারে ব্যবহার করেছি সাবপ্রবলেমের রেজাল্টগুলো সেভ করে রাখতে। একদম শুরুতে অ্যারেতে এমন ভ্যালু রাখতে হবে যেটা কখনোই উত্তর হওয়া সম্ভব না, এক্ষেত্রে আমরা $-1$ ব্যবহার করছি। প্রতিবার রিকার্সিভ ফাংশন কল করার আগে দেখছি যে সাবপ্রবলেমটার সমাধান অ্যারেতে এরই মধ্যে রাখা আছে নাকি, থাকলে সেটা রিটার্ন করে দিচ্ছি। আর না থাকলে সাবপ্রবলেমের রেজাল্ট ক্যালকুলেট করে আগে অ্যারেতে সেভ করছি এবং তারপর রিটার্ন করছি।
এবার আমাদের কোডের টাইম কমপ্লেক্সিটি হয়ে যাচ্ছে $O(n)$ কারণ আমাদের $n$ টা সাবপ্রবলেম আছে যেগুলো হলে $f(0), f(1) …. f(n)$ এবং প্রতিটা সাবপ্রবলেম আমরা মাত্র ১বার সমাধান করছি। রিকার্সিভ ফাংশন কল করা ছাড়া আর কোনো কাজ আমরা এই ফাংশনে করিনি, করলে সেটার টাইম কমপ্লেক্সিটিও গুণ হতো, সেটা আমরা পরের প্রবলেমেই দেখবো।
এভাবে সাবপ্রবলেমের রেজাল্ট সেভ করে রাখার একটা নাম আছে, সেটা হলো Memoization। ল্যাটিন ভাষার শব্দ memorandum থেকে এই শব্দটা তৈরি করেন Donald Mitchie নামক একজন এ.আই রিসার্চার, ইংরেজি memorization শব্দটির সাথে এর তেমন একটা পার্থক্য নেই।
ডাইনামিক প্রোগ্রামিং এর কোড রিকার্সিভ হতে হবে এমন কোন কথা নেই। ইটারেটিভ কোড লিখতে সাবপ্রবলেম গুলোকে মনে মনে টপোলজিকাল অর্ডারে সাজিয়ে নিতে হবে এবং যে সাবপ্রবলেমের উত্তর আমাদের জানা আছে (base case) সেখান থেকে রেজাল্ট বিল্ডআপ করতে হবে। টপোলোজিকাল অর্ডার মানে হলো কতগুলো ঘটনাকে কোনটার উপর কোনটা নির্ভরশীল সেই অর্ডারে সাজানো।
ফিবোনাচ্চির ক্ষেত্রে আমরা $f(0), f(1)$ এর রেজাল্ট আগে থেকেই জানি। আমরা এই দুটো ভ্যালুকে টেবিলে সেভ করে $f(2), f(3) …. f(n)$ এই অর্ডারে রেজাল্ট বিল্ডআপ করতে পারি।
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#define MAX_N 20 int memo[MAX_N + 1]; int f(int n) { memo[0] = 0; memo[1] = 1; for(int i = 2;i <= n;i++) { memo[n] = memo[i - 1] + memo[i - 2]; } return memo[n]; } |
ডাইনামিক প্রোগ্রামিং সমাধান করার সময় তোমাকে শুরুতে মনে মনে বা খাতায় রিকার্সিভ সমীকরণ বের করে নিতে হবে। এরপর তুমি চাইলে কোড রিকার্সিভ বা ইটারেটিভ ভাবে লিখতে পারে। রিকার্সিভ ভাবে কোড লেখা খুবই সহজ, সমীকরণটাকেই কোড হিসাবে লিখে দিলে ম্যাজিকের মত সমাধান বের করে আনবে। ইটারেটিভ ভাবে লিখতে হলে তোমাকে সাবপ্রবলেমের অর্ডারিং নিয়ে চিন্তা করতে হবে যেটা একটু কঠিন হয়ে যায় যদি সাবপ্রবলেমের একাধিক প্যারামিটার থাকে। তবে ইটারেটিভ পদ্ধতিও আমাদের জানা থাকতে হবে কারণ ইটারেটিভ পদ্ধতিতে অনেক সময়ই স্পেস অপটিমাইজ করা যায়। যেমন উপরের কোডেই আমাদের অ্যারের ঠিক আগের দুটি ভ্যালু ছাড়া বাকিগুলো কোনো কাজে লাগছে না, তাই $n$ সাইজের অ্যারের কোনো দরকার নাই।
ডাইনামিক প্রোগ্রামিং প্রবলেম অ্যাটাক করার কিছু নিয়ম আছে, আমরা সেই নিয়ম মেনে চিন্তা করতে শিখলেই কোন প্রবলেম ডাইনামিক প্রোগ্রামিং দিয়ে সমাধান করা যাবে এবং কিভাবে সমাধানটা বের করা যাবে সেটা বুঝে যাবো। ফিবোনাচ্চি খুব সহজ উদাহরণ হলেও খুব ভালো উদাহরণ না কারণ এখানে কোন কিছু অপটিমাইজ করা হয় না। পরের পর্বে আমরা একটা অপটিমাইজেশন প্রবলেম দেখবো যেটা আমাদের ডিপির ধারণা আরো পরিস্কার করে দিবে।
ফেসবুকে মন্তব্য
Powered by Facebook Comments
DP শুরু করার জন্য এর থেকে ভাল tutorial সম্ভব না। খুবই সাধারণ ভাবে লেখা। এটা বোঝার জন্য আগে থেকে খুব ভাল programming বা algorithm না জানলেও চলে। খালি recursion জানলেই যথেষ্ট ।
@সিয়াম: অসংখ্য ধন্যবাদ :)।
খুব সুন্দর লেখা 🙂
তবে থেমে যেও না,কন্টিনিউ কইর 🙂
রিকার্শনটি হলো nCr =(n-1)Cr + (n-1)C(r-1)।
কিন্তু nCr =nC(r-1) + (n-1)C(r-1)এটা নই। just a mistake.
@martuza: ঠিক করে দিলাম,থ্যাংকস।
programming contest er jonno gora theke shuru korte chai . sahajjo pele khusi hobo vai,ar apnio jodi khuti nati soho kono post blog e dan .dhonnobad.
shafaet.csedu[at]gmail.com এই ঠিকানায় মেইল করতে পারো,সাহায্য করতে পারলে খুশি হবো। চেষ্টা করবো ভবিষ্যতে এটা নিয়ে পোস্ট দিতে।
ভাইয়া আমি এই ব্লগ এ এই প্রথম । কিন্তু প্রথম দেখায় ই প্রেমে পড়ে গেলাম । LOVE AT FIRST SIGHT . সত্যিই দারুন সুন্দর একটা ব্লগ । এখন থেকে fan হয়ে গেলাম । 🙂
অনেক বেশি সুন্দর 😀
লেখাটা পড়া শুরু করার আগেই ফাহিম ভাইয়ের লেখাটা পইড়া আসলাম! উনার ঐখানে কমেন্টের কোনো অপশন নাই তাই এইখানেই লেখি! অসধারন লাগলো উনার আর্টিকেলটা, খুবই মজা কইরা লেখছেন! লিংকটা দেওয়ার জন্য আপনারেও ধন্যবাদ!
অস্থির !! ভাল হয়েছে। 🙂
1006 – Hex-a-bonacci পারতেছি না।
চমংকার হয়েছে
অসাধারন। সেমিস্টার ব্রেকে ডিপি শেখার ইচ্ছা ছিল! এখন ইচ্ছা পূরন হয়ে যাবে মনে হচ্ছে! 😀
ভাইয়া আমি সুবিন ভাইয়ের বইটা শেষ করেছি । এখন হার্ভার্ড শিল্ডের Teach yourself C পড়ছি । আমি সেটা পড়ে শেষ করে তারপর এগুলো পড়বো, নাকি এখনই শুরু করে দেবো । সমস্যা হচ্ছে যে সুবিন ভাই তাঁর বইয়ে 3d অ্যারে সম্বন্ধে উল্লেখ করেন নি । 🙂
Thanks Brother 😀
onak helpful
1006 – Hex-a-bonacci Accepted !!
খুব ভাল লাগল !
It is really helpful for all beginner.
খুবই ভাল একটি ব্লগ।
Just love it….
Homework and Lightoj 1006 Both done…
Looking Forwrd to reading your second blog 😀
ডাইনামিক প্রোগ্রামিং এর ক্লাসিকাল এলগরিদম গুলো কিভাবে কাজ করে সেটা জেনে নন ক্লাসিকাল সল্ভ করা নাকি শুরুতেই ক্লাসিকাল অথবা নন ক্লাসিকাল ডিপি প্রব্লেম নিজে নিজে সল্ভ করা উচিৎ ?
ইটারেটিভ DP এর ক্ষেত্রে এই লাইনটাঃ
memo[n] = memo[n – 1] + memo[n – 2];
memo[i] = memo[i – 1] + memo[i-2];
হওয়ার কথা না??
ঠিক করে দিয়েছি, ধন্যবাদ।
আরেকটা ভুল ছিল, i = 2 থেকে লুপ শুরু হবে।
iterative er khetre
i <= n hower kotha na?