আমরা এরই মধ্যে ডাইনামিক প্রোগ্রামিং এর বেসিক শিখে গিয়েছি, আমরা ফিবোনাচ্চি এবং DAG এ শর্টেস্ট পাথ বের করতে পারি। এবার আমরা শিখবো Longest Increasing Subsequence বা LIS বের করা। এতদিন আমরা শুধু অপটিমাল সলিউশনটা বের করতে শিখেছি, কোন পথ ধরে সলিউশনে পৌছাতে হয় সেটা বের করা শিখিনি। এবার আমরা নেক্সট-পয়েন্টার ব্যবহার করে সেটা বের করাও শিখবো।
ধরা যাক আমাদের নিচের ছবির মতো একটা অ্যারে আছে যার নাম $A$।
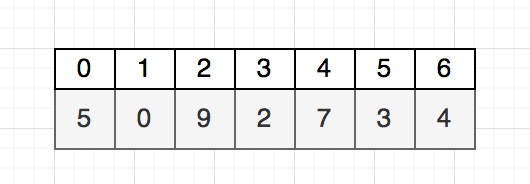একটা অ্যারের সাবসিকোয়েন্স বলতে বুঝায় অ্যারে থেকে কিছু এলিমেন্ট মুছে দিলে বাকি যে সিকোয়েন্সটা থাকে সেটা। এলিমেন্টগুলোর অর্ডারিং পরিবর্তন করা যাবে না। $n$ সাইজের একটা অ্যারের $2^{n}$ টি সাবসিকোয়েন্স থাকতে পারে (প্রতিটা এলিমেন্টের জন্য ২টি চয়েস, রেখে দেয়া বা মুছে দেয়া)। ইনক্রিসিং সাবসিকোয়েন্স হলো এমন একটা সাবসিকোয়েন্স যার প্রতিটি পজিশনের ভ্যালু আগের পজিশনের ভ্যালুর থেকে বড়।
উপরের উদাহরণে $\{0, 9\}, \{5,9\}, \{0, 2, 7\}, \{0, 2, 3, 4\}$ কিছু ইনক্রিসিং সাবসিকোয়েন্স। সবথেকে লম্বা ইনক্রিসিং সাবসিকোয়েন্স বা LIS হলো $\{0, 2, 3, 4\}$। প্রথমে আমরা চেষ্টা করবো LIS এর দৈর্ঘ্য বের করতে, এরপরে মূল সাবসিকোয়েন্সটাও ট্র্যাক করা শিখবো।
প্রবলেমের প্যারামিটার বা স্টেট নির্ধারণ:
আমরা প্রবলেমটা এভাবে চিন্তা করতে পারি: আমরা বর্তমানে ইনডেক্স $i$ তে আছি এবং আমাদেরকে সবথেকে লম্বা সাবসিকোয়েন্স বের করতে হবে যেটা $i$ তম ইনডেক্স থেকে শুরু হয়েছে। ধরা যাক $f(i)$ ফাংশনটা সেই জিনিসটা তোমাকে ক্যালকুলেট করে দিতে পারে। এখন আগের মতো $f(0)$ বের করলেই কি হবে? হবে না কারণ আমরা জানিনা LIS ঠিক কোন ইনডেক্স থেকে শুরু হয়েছে। আমাদেরকে ফাইনাল রেজাল্ট হবে হবে – $max(f(0), f(1) …. f(n – 1))$।
স্টেট ট্রানজিশন এবং রিকার্শন:
এখন আমরা জানিনা ইনডেক্স $i$ থেকে কোন ইনডেক্সে গেলে আমরা সব থেকে লম্বা সাবসিকোয়েন্স পাবো। এখন আমাদেরকে অনুমান করতে হবে। $i$ থেকে যে যে ইনডেক্সে যাওয়া যায় সবগুলোয় গিয়ে গিয়ে আমরা দেখবো সেখান থেকে LIS এর দৈর্ঘ্য কত এবং যেটা সবথেকে লম্বা সেটাকে বেছে নিবো।
ইনডেক্স $i$ থেকে কোন কোন ইনডেক্সে যাওয়া যায়? $j$ ইনডেক্সকে দুটো শর্ত পূরণ করতে হবে:
- যেহেতু অর্ডার মেইনটেইন করতে হবে, তাই নতুন ইনডেক্স $j$ অবশ্যই $i$ এর থেকে বড় হবে $(i < j < n)$।
- সেই সাথে A[j] এর মানও A[i] থেকে বড় হতে হবে $(A[j] > A[i])$।
অর্থাৎ $(i < j < n) & (A[j] > A[i])$ হলেই শুধুমাত্র আমরা $i$ থেকে $j$ তে যেতে পারবো। রিকার্শনটা তাহলে হবে এরকম
$f(i) = 1 + max(f(j))\ where\ i < j < n \ \&\ A[j] > A[i]$
কনফিউজড লাগছে? আগের শর্টেস্ট পাথ প্রবলেমের মত মনে করো প্রতিটা ইনডেক্স একটা করে শহর। এবার কোন শহর থেকে কোন শহরে যাওয়া যায় সেটা অ্যারো টেনে দেখিয়ে দাও উপরের শর্ত মেনে।
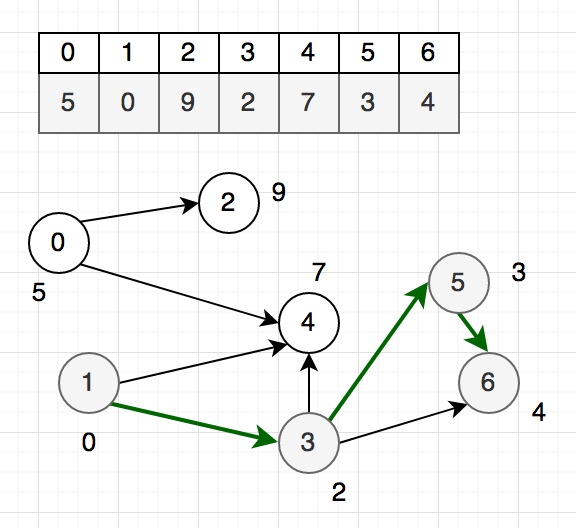অ্যারেটাকে আমরা গ্রাফ দিয়ে মডেলিং করলাম ভিজুয়ালাইজেশনের জন্য। আমাদের প্রবলেমটা এখন হয়ে গেলো ডিরেক্টেড অ্যাসাইক্লিক গ্রাফে লংগেস্ট পাথ বের করা!
লক্ষ্য করো আমাদের রিকার্শনে কোনো বেস কেস ডিফাইন করিনি। এই প্রবলেমে সেটা দরকার নেই কারণ এক স্টেট থেকে আরেক স্টেটে এমন ভাবে যাচ্ছি যে রিকার্শন এমনিই থেমে যাবে শেষে গিয়ে (আমরা সবসময় অ্যারের সামনে আগাচ্ছি, একসময় আর আগানো যাবে না)। রিকার্শন লুপে পড়ারও কোনো সম্ভাবনা নেই।
কোডটা লিখে ফেলি:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
#define MAX_N 20 #define EMPTY_VALUE -1 int mem[MAX_N]; int f(int i, vector<int> &A) { if (mem[i] != EMPTY_VALUE) { return mem[i]; } int ans = 0; for (int j = i + 1;j < A.size();j++) { if (A[j] > A[i]) { ans = max(ans, f(j, A)); } } mem[i] = ans + 1; return mem[i]; } int findLIS(vector<int> A){ int ans = 0; for(int i = 0;i<A.size();i++) { mem[i] = EMPTY_VALUE; } for(int i = 0;i<A.size();i++) { ans = max(ans, f(i, A)); } return ans; } |
কমপ্লেক্সিটি: শর্টেস্ট পাথ প্রবলেমের মতোই এটারও কমপ্লেক্সিটি $O(n*n)$। ভিন্ন ভিন্ন স্টেট আছে $n$ টা এবং প্রতিটি স্টেটের জন্য $n$ সাইজের লুপ চালাতে হচ্ছে।
ইটারেটিভ ভার্সন:
প্রবলেমটা আমরা শর্টেস্ট পাথের মত ফর্মুলায় ফেললেও এবার ইটারেটিভ ভার্সন লেখা খুব একটা কঠিন না। স্টেটগুলোকে টপলোজিকাল অর্ডারে সাজাতে গেলে দেখবে সবসময় আমরা ছোট থেকে বড় ইনডেক্সে যাচ্ছি। $n-1, n-2 …., 1, 0$ এই অর্ডারে ইটারেটিভলি ডিপি টেবিল বিল্ডআপ করা যায় খুব সহজেই।
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
int lisIterative(vector<int> A) { for (int i = A.size() - 1;i >= 0;i--) { int ans = 0; for (int j = i + 1;j < A.size();j++) { if (A[j] > A[i]) { ans = max(ans, mem[j]); } } mem[i] = ans + 1; } int final_ans = 0; for(int i = 0;i<A.size();i++) { final_ans = max(final_ans, mem[i]); } return final_ans; } |
খেয়াল করো এবার আমাদেরকে আর mem টেবিলটা $-1$ দিয়ে ভরে নিতে হচ্ছে না। $i$ এর লুপটার ভিতরে বাকি অংশটা অনেকটা রিকার্সনের মতোই। $i$ এর লুপটা 0 থেকে শুরু করলে কোডটা কাজ করতো না।
সলিউশনের পাথ প্রিন্টিং
ইটারেটিভ বা রিকার্সিভ দুই পদ্ধতিতেই পাথ প্রিন্টিং এর নিয়ম একই। আমাদেরকে আরেকটা টেবিল মেইনটেইন করতে হবে যার নাম হতে পারে next_pointer। যখনই কোন সাবপ্রবলেম একটু বেটার রেজাল্ট দিবে তখনই টেবিলে সেভ করে রাখতে হবে কোন স্টেট থেকে কোন স্টেটে যাচ্ছি। সবশেষে প্রথম স্টেট থেকে নেক্সট পয়েন্টার ধরে ধরে পাথ খুজে বের করা যাবে।
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
#define MAX_N 20 #define EMPTY_VALUE -1 int mem[MAX_N]; int next_index[MAX_N]; int f(int i, vector<int> &A) { if (mem[i] != EMPTY_VALUE) { return mem[i]; } int ans = 0; for (int j = i + 1;j < A.size();j++) { if (A[j] > A[i]) { int subResult = f(j, A); if (subResult > ans) { ans = subResult; next_index[i] = j; } } } mem[i] = ans + 1; return mem[i]; } vector<int> findLIS(vector<int> A){ int ans = 0; for(int i = 0;i<A.size();i++) { mem[i] = EMPTY_VALUE; next_index[i] = EMPTY_VALUE; } int start_index = -1; for(int i = 0;i<A.size();i++) { int result = f(i, A); if (result > ans) { ans = result; start_index = i; } } vector<int> lis; while(start_index != -1) { lis.push_back(A[start_index]); start_index = next_index[start_index]; } return lis; } |
তাহলে এই পর্বে তুমি শিখলে:
- ডিপির প্রবলেমকে গ্রাফ দিয়ে ভিজুয়ালাইজেশন করলে কোন স্টেট থেকে কোন স্টেটে যাবে বুঝতে সুবিধা হয়।
- প্রতিটা স্টেটের জন্য নেক্সট পয়েন্টার রেখে রেখে পাথ প্রিন্ট করা যায়।
প্র্যাকটিস প্রবলেম:
https://leetcode.com/problems/longest-increasing-subsequence/
https://leetcode.com/problems/maximum-length-of-pair-chain/
এরপরে আমরা কিছু ডিপি দেখবো যেখানে একাধিক স্টেট ব্যবহার করতে হয়। আজকে এই পর্যন্তই।
ফেসবুকে মন্তব্য
Powered by Facebook Comments
How Many Dependencies? প্রবলেমে বলা আছে ‘You can assume there will be no cyclic dependencies in the input’ । কিন্তু আমার মনে হয় সাইকেল আছে । কারণ আমি ভিসিটেড অ্যারে ছাড়া কয়েকবার ট্রাই করে টিএলই খাইছি :\
getting TLE. need your guidelines. my codes at: http://ideone.com/WBy8XA
sorry, I forgot to mention the problem. http://acm.timus.ru/problem.aspx?space=1&num=1501
How many dependencies প্রব্লেম টা সল্ভ করতে পারতেছি না। WA । এইটা কি LIS দিয়ে সম্ভব সমাধান করা?