তুমি যখন একটা অ্যালগরিদমকে কোডে ইমপ্লিমেন্ট করবে তার আগে তোমার জানা দরকার অ্যালগরিদমটি কতটা কার্যকর। অ্যালগোরিদম লেখার আগে নিজে নিজে কিছু প্রশ্নের উত্তর দিতে হবে,যেমন:
১. আমার অ্যালগোরিদম কি নির্ধারিত সময়ের মধ্যে ফলাফল এনে দিবে?
২. সর্বোচ্চ কত বড় ইনপুটের জন্য আমার অ্যালগোরিদম কাজ করবে?
৩. আমার অ্যালগোরিদম কতখানি মেমরি ব্যবহার করছে?
আমরা অ্যালগোরিদমের কমপ্লেক্সিটি বের করে প্রথম দুটি প্রশ্নের উত্তর দিতে পারি। একটি অ্যালগরিদম যতগুলো “ইনস্ট্রাকশন” ব্যবহার করে কাজ করে সেটাই সোজা কথাই সেই অ্যালগোরিদমের কমপ্লেক্সিটি। দুটি নম্বর গুণ করা একটি ইনস্ট্রাকশন, আবার একটি লুপ ১০০ বার চললে সেখানে আছে ১০০টি ইনস্ট্রাকশন। ফলাফল আসতে কতক্ষণ লাগবে সেটা সিপিউর প্রসেসরের উপর নির্ভর করবে, কমপ্লেক্সিটি আমাদের cputime বলে দিবেনা, কমপ্লেক্সিটি আমাদের বলে দিবে আমাদের অ্যালগরিদমটি তুলনামূলকভাবে কতটা ভালো। অর্থাৎ এটা হলো অ্যালগরদিমের কার্যকারিতা নির্ধারণের একটা স্কেল। আর BIG $O$ নোটেশন হলো কমপ্লেক্সিটি লিখে প্রকাশ করার নোটেশন।
আমরা একটা উদাহরণ দিয়ে শুরু করি। আমাদের একটি ফাংশন আছে যার নাম $myAlgorithm$,আমরা সেই ফাংশনের কমপ্লেক্সিটি বের করবো। মনে করো ফাংশনটি এরকম:
|
1 2 3 4 5 6 |
int myAlgorithm1(int n) { int x=n+10; x=x/2; return x; } |
এই অ্যালগোরিদমটি $n$ এর ভ্যালু যাই হোকনা কেন সবসময় একটি constant সংখ্যক ইনস্ট্রাকশন নিয়ে কাজ করবে। কোডটিকে মেশিন কোডে পরিণত করলে যোগ-ভাগ মিলিয়ে ৩-৪ ইনস্ট্রাকশন পাওয়া যাবে,আমাদের সেটা নিয়ে ম্যাথাব্যাথার দরকার নাই। প্রসেসর এত দ্রুত কাজ করে যে এত কম ইনস্ট্রাকশন নিয়ে কাজ করতে যে সময় লাগে সেটা নিয়ে আমরা চিন্তাই করিনা,ইনস্ট্রাকশন অনেক বেশি হলে আমরা চিন্তা করি,আর লুপ না থাকলে সাধারণত চিন্তা করার মত বেশি হয়না।
অ্যালগোরিদমের কমপ্লেক্সিটি হলো $O(1)$,এর মানে হলো ইনপুটের আকার যেমনই হোকনা কেন একটি constant টাইমে অ্যালগোরিদমটি কাজ করা শেষ করবে।
এবার পরের কোডটি দেখ:
|
1 2 3 4 5 6 7 8 9 10 |
int myAlgorithm2(int n) { int sum=0; for(int i=1;i<=n;i++) { sum+=i; if(sum>=1000) break; } return sum; } |
এই কোডে একটি লুপ চলছে এবং সেটা $n$ এর উপর নির্ভরশীল। $n=100$ হলে লুপ ১০০ বার চলবে। লুপের ভিতরে বা বাইরে কয়টি ইনস্ট্রাকশন আছে সেটা নিয়ে চিন্তা করবোনা,কারণ সেটার সংখ্যা খুবই কম। উপরের অ্যালগোরিদমের কমপ্লেক্সিটি $O(n)$ কারণ এখানে লুপটি $n$ বার চলবে। তুমি বলতে পারো sum যদি ১০০০ এর থেকে বড় হয় তাহলে break করে দিচ্ছি, $n$ পর্যন্ত চলার আগেই লুপটি break হয়ে যেতে পারে। কিন্তু প্রোগ্রামাররা সবসময় worst case বা সবথেকে খারাপ কেস নিয়ে কাজ করে! এটা ঠিক যে লুপটি আগে break করতেই পারে,কিন্তু worst case এ সেটা $n$ পর্যন্তইতো চলবে।
worst case এ যতগুলো ইনস্ট্রাকশন থাকবে সেটাই আমাদের কমপ্লেক্সিটি।
|
1 2 3 4 5 6 7 8 9 10 11 12 |
int myAlgorithm3(int n) { int sum=0; for(int i=1;i<=n;i++) { for(int j=i;j<=n;j++) { sum+=(i+j); } } return sum; } |
উপরের কোডে ভিতরের লুপটা প্রথমবার $n$ বার চলছে,পরেরবার $n-1$ বার। তাহলে মোট লুপ চলছে $n+(n-1)+(n-3)+…….+1 = n \times (n+1)/2 = (n^2+n)/2$ বার। $n^2$ এর সাথে $n^2+n$ এর তেমন কোনো পার্থক্য নেই। আবার $n^2/2$ এর সাথে $n^2$ এর পার্থক্যও খুব সামান্য। তাই কমপ্লেক্সিটি হবে $O(n^2)$।
কমপ্লেক্সিটি হিসাবের সময় constant factor গুলোকে বাদ দিয়ে দিতে হয়। তবে কোড লেখার সময় constant factor এর কথা অবশ্যই মাথায় রাখতে হবে।
উপরের ৩টি অ্যালগোরিদমের মধ্যে সবথেকে সময় কম লাগবে কোনটির? অবশ্যই $O(1)$ এর সময় কম লাগবে এবং $O(n^2)$ এর বেশি লাগবে। এভাবেই কমপ্লেক্সিটি হিসাব করে অ্যালগোরিদমের কার্যকারিতা তুলনা করা যায়। পরের কোডটি দেখো:
|
1 2 3 4 5 6 7 8 9 10 11 12 |
int myAlgorithm4(int n,int *val,int key) { int low=1,high=n; while(low<=high) { int mid=(low+high)/2; if(key<val[mid]) low=mid-1; if(key>val[mid]) high=mid+1; if(key==val[mid]) return 1; } return 0; } |
এটা একটা বাইনারি সার্চের কোড। প্রতিবার $low+high=n+1$ বা $n$ এর মান দুই ভাগে ভাগ হয়ে যাচ্ছে। একটি সংখ্যাকে সর্বোচ্চ কতবার ২দিয়ে ভাগ করা যায়? একটি হিসাব করলেই বের করতে পারবে সর্বোচ্চ ভাগ করা যাবে $log_2{n}$ বার। তারমানে $log_2{n}$ ধাপের পর লুপটি ব্রেক করবে। তাহলে কমপ্লেক্সিটি হবে $O(log_2{n})$।
এখন ধরো একটি অ্যালগোরিদমে কয়েকটি লুপ আছে,একটি $n^4$ লুপ আছে,একটি $n^2$ লুপ আছে আর একটি $log{n}$ লুপ আছে। তাহলে মোট ইনস্ট্রাকশন: $n^4+n^3+log{n}$ টি। কিন্তু $n^4$ এর তুলনায় বাকি টার্মগুলো এতো ছোটো যে সেগুলোকে বাদ দিয়েই আমরা কমপ্লেক্সিটি হিসাব করবো, $O(n^4)$।
রিকার্সিভ ফাংশনে depth এর উপর কমপ্লেক্সিটি নির্ভর করে,যেমন:
|
1 2 3 4 5 |
int myAlgorithm5(int n) { if(n==1) return 1; return n*myAlgorithm5(n-1); } |
এই অ্যালগোরিদমে সর্বোচ্চ depth হলো $n$,তাই কমপ্লেক্সিটি হলো $O(n)$। নিচে ছোট করে আরো কিছু উদাহরণ দিলাম:
$f(n)$=ইনস্ট্রাকশন সংখ্যা
$f(n) = n^2 + 3n + 112$ হলে কমপ্লেক্সিটি $O(n^2)$।
$f(n) = n^3 + 999n + 112$ হলে কমপ্লেক্সিটি $O(n^3)$।
$f(n) = 6 \times log(n) + n \times logn$ হলে কমপ্লেক্সিটি $O(n \times logn)$।
$f(n)$ = $2^n+n2+100$ হলে কমপ্লেক্সিটি $O(2^n)$। (এটাকে exponential কমপ্লেক্সিটি বলে)
বিগিনারদের আরেকটি কমন ভুল হলো এভাবে কোড লেখা:
|
1 2 3 4 5 6 7 8 9 |
int myAlgorithm6(char *s) { int c=0; for(int i=0;i<strlen(s);i++) { if(s[i]=='a') c++; } return c; } |
s স্ট্রিং এর দৈর্ঘ্য |s| হলে এখানে কমপ্লেক্সিটি হলো $O(|s|^2)$। কেন স্কয়ার হলো? কারণ strlen(s) ফাংশনের নিজের কমপ্লেক্সিটি হলো $O(|s|)$,একে লুপের মধ্যে আরো $O(|s|)$ বার কল করা হয়েছে। তাই strlen(s) এর মান আগে অন্য একটি ভ্যারিয়েবলের রেখে তারপর সেটা দিয়ে লুপ চালাতে হবে,তাহলে $O(|s|)$ এ লুপ চলবে।
প্রোগ্রামিং কনটেস্টে আমরা ধরে নেই জাজ এর পিসি ১ সেকেন্ডে মোটামুটি $10^8$ টা ইনস্ট্রাকশন রান করতে পারবে। এটা জাজ-পিসি অনুসারে কমবেশি হতে পারে,যেমন টপকোডার আরো অনেক বেশি ইনস্ট্রাকশন ১ সেকেন্ডে রান করতে পারে কিন্তু spoj বা কোডশেফ তাদের পেন্টিয়াম ৩ পিসি দিয়ে $10^7$ টাও সহজে রান করতে পারেনা। অনসাইট ন্যাশনাল কনটেস্টে আমরা ১ সেকেন্ডে $10^8$ ধরেই কোড লিখি। কোড লেখার আগে প্রথমে দেখবে তোমার অ্যালগোরিদমের worst case কমপ্লেক্সিটি কত এবং টেস্ট কেস কয়টা এবং দেখবে টাইম লিমিট কত। অনেক নতুন প্রোগ্রামার অ্যালগোরিদমের কমপ্লেক্সিটি সঠিক ভাবে হিসাব করলেও টেস্ট কেস সংখ্যাকে গুরুত্ব দেয়না,এ ব্যাপারে সতর্ক থাকতে হবে।
নিচের গ্রাফে বিভিন্ন কমপ্লেক্সিটির অ্যালগোরিদমের তুলনা দেখানো হয়েছে:
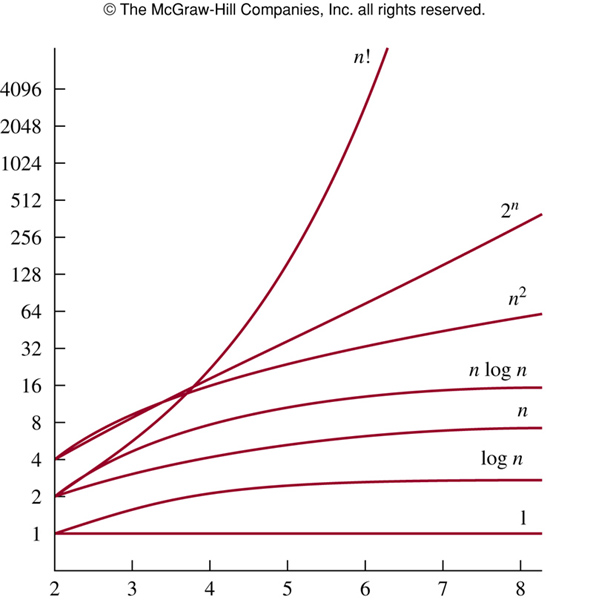
(x axis=input size, y axis=number of instructions)
কনটেস্টে প্রবলেমের ইনপুট সাইজ দেখে অনেক সময় expected algorithm অনুমান করা যায়। যেমন n=100 হলে সম্ভাবনা আছে এটা একটা n^3 কমপ্লেক্সিটির ডিপি প্রবলেম,বা ম্যাক্সফ্লো-ম্যাচিং প্রবলেম। n=10^5 হলে সাধারণ nlogn কমপ্লেক্সিটিতে প্রবলেম সলভ করতে হয় তাই সম্ভাবনা আছে এটা একটা বাইনারি সার্চ বা সেগমেন্ট ট্রি এর প্রবলেম।
আজ এই পর্যন্তই। কমপ্লেক্সিটি নিয়ে আরো অনেক কিছু জানার আছে,বিস্তারিত পড়তে:
A Gentle Introduction to Algorithm Complexity Analysis
Complexity and Big-O Notation
ফেসবুকে মন্তব্য
Powered by Facebook Comments

জিনিসটা খুব দরকারি ছিল! সবাই খালি অ্যালগোরিদম নিয়ে লাফায় কিন্তু complexity নিয়ে কেউ চিন্তা করে না অথচ আলগোরিদমের সাথে সাথে complexity জানাও খুব জরুরি। দারুণ একটা লেখা।
ধন্যবাদ :)।
কমপ্লেক্সিটি আগেই হয়ত বের করতে পারতাম কিন্তু এটা পড়ে ধারনাটা আরেকটু পরিস্কার হল। ইনপুট সাইজ দেখে expected algorithm অনুমান করা যায় – এভাবে কখনো ভাবিনি আগে। ধন্যবাদ । 🙂
ধন্যবাদ। এই অনুমানটা কনটেস্ট খুবই কাজে লাগে। প্রবলেমসেটাররা সাধারণত এমনভাবে ইনপুট সাইজ দেয় যাতে আমাদের একটা ভালো অ্যালগোরিদম টেকনিক ব্যবহার করা দরকার হয়। যে ডিপি n^2 এ সলভ করা যায় সেটায় সাধারণত n এর মান তারা ১০০ দিবেনা,তাহলে বাজে কোনো n^3 সলিউশনও পাস করে যাবে,তারা হয় n এর মান দিবে ১০০০,অথবা টেস্ট কেস সংখ্যা বাড়িয়ে দিবে যাতে n^3 পাস না করে।
শাফায়েত, আপনার পোস্টটা কোডগুলোর সাথে মিলিয়ে মিলিয়ে দেখলাম। এখন হিসাবটা মোটামুটি বোঝা গেছে। এই বিগ O নোটেশন যে কতবার এড়িয়ে গিয়েছ 🙂 …যদিও পাইথনে প্রোগ্রামিঙ এই বছরই শিখলাম, তবুও কোডগুলো বুঝতে কষ্ট হলো না। উদাহরণ কি সি প্লাস প্লাসে করা?
ঠিক এই রকমের একটা টিউটোরিয়াল ইংরেজিতে দেখেছিলাম, bid O নোটেশনের উপর। ভালো লাগছে যে শুধুমাত্র এলগরিদম নিয়ে একটি ব্লগ আছে … শুধু তাই নয়, তার নির্দিষ্ট একটা পাঠকদলও আছে। এটা সত্যিই বাংলা ভাষায় বিজ্ঞানচর্চার ক্ষেত্রে অনেক বড় একটা ব্যাপার … the wind is changing …
ভালো থাকুন।
বিগ O শিখতে আমার ব্লগে চলে এসেছেন দেখে খুব ভালো লাগলো। আশা করি এটা আপনার স্ক্রিপ্টিং এর কাজে সাহায্য করবে। আর হ্যা কোডগুলো সি++ এ লেখা।
= n*(n+1)/2 = (n^2+1)/2 বার
how?
n^2+n হবে, ধন্যবাদ।
আপনার গুরুত্বপূর্ণ লেখাটির জন্য ধন্যবাদ।
খুব ভালো লিখেছেন।
আমার ১তা ছোট প্রশ্ন ছিল uva prob 10611 C++ ছাড়া মানে vector,map use করা ছাড়া সি তে কিভাবে করা যাই ?
ভাইয়া for(int i=1;i<=n;i++) চদেগুলোতে for loop এর ভিতরে int i এর মাধ্যমে কি i কে declare করছেন???
ভাইয়া for(int i=1;i<=n;i++) কোড গুলোতে for loop এর ভিতরে int i এর মাধ্যমে কি i কে declare করছেন???
ভালো লাগলো
মনে করেন একটা প্রবলেম এর টেস্ট কেইস ১০০, ইনপুট সাইজ ৫০। মানে টেস্ট কেইস এর ভিতরে লুপটা ৫০ বার ঘুড়বে। তাহলে এটার কমপ্লেক্সিটি কি ৫০ হবে নাকি ১০০*৫০ = ৫০০০০ হবে?
tnx safayet vai.
নরমালি কম্পিউটারে ছোট প্রোগ্রাম চালালে দেখা যায় process terminated in ‘x’ second. এইটাই কি টাইম কমপ্লেক্সিটি ?
একটি সংখ্যাকে সর্বোচ্চ কতবার ২দিয়ে ভাগ করা যায়? একটি হিসাব করলেই বের করতে পারবে সর্বোচ্চ ভাগ করা যাবে.
log2n বার. how?
পোস্টটি অনেক উপকারী
ধন্যবাদ উপকারী পোষ্টের জন্য