(গ্রাফ অ্যালগরিদম বইটি অনলাইনে পাওয়া যাচ্ছে রকমারি.কম এ। এছাড়াও নীলক্ষেতে হক, মানিক এবং রানা লাইব্রেরিতে বইটি পাওয়া যাচ্ছে)

তুমি কি জানো পৃথিবীর প্রায় সব রকমের প্রবলেমকে কিছু রাস্তা আর শহরের প্রবলেম বানিয়ে সলভ করে ফেলা যায়? গ্রাফ থিওরির যখন জন্ম হয় তখন তোমার আমার কারোই জন্ম হয়নি, এমনকি পৃথিবীতে কোন কম্পিউটারও ছিলোনা! সেই সতেরো দশকের শেষের দিকে লিওনার্দ অয়লার গ্রাফ থিওরি আবিষ্কার করেন কনিসবার্গের সাতটি ব্রিজের সমস্যার সমাধান করতে। তখনই সবার কাছে পরিস্কার হয়ে যায় যে যেকোন প্রবলেমকে শহর-রাস্তার প্রবলেম দিয়ে মডেলিং করে চেনা একটা প্রবলেম বানিয়ে ফেলতে গ্রাফ থিওরির জুড়ি নেই। আর যখনই তুমি একটা প্রবলেমকে চেনা কোন প্রবলেমে কনভার্ট করে ফেলতে পারবে তখন সেটা সমাধান করা অনেক সহজ হয়ে যাবে।

গ্রাফ থিওরির অনেক অ্যাপ্লিকেশন আছে। সবথেকে কমন হলো এক শহর থেকে আরেক শহরে যাবার দ্রুততম পথ খুজে বের করা। তুমি হয়তো জানো সার্ভার থেকে একটা ওয়েবপেজ তোমার পিসিতে পৌছাতে অনেকগুলো রাউটার পার করে আসতে হয়, গ্রাফ থিওরি দিয়ে এক রাউটার থেকে আরেকটাতে যাবার পথ খুজে বের করা হয়। যুদ্ধের সময় একটা দেশের কোন কোন রাস্তা বোমা দিয়ে উড়িয়ে দিলে দেশের রাজধানী সব শহর থেকে বিচ্ছিন্ন হয়ে যাবে সেটাও বের করে ফেলা যায় গ্রাফ থিওরি দিয়ে। আমরা গ্রাফ অ্যালগোরিদমগুলো শেখার সময় আরো অনেক অ্যাপ্লিকেশন দেখবো।

আমাদের এই হাতেখড়ির লক্ষ্য হবে প্রথমেই গ্রাফ থিওরির একদম বেসিক কিছু সংজ্ঞা জানা, তারপর কিভাবে গ্রাফ মেমরিতো স্টোর করতে হয় সেটা জানা, এরপরে গ্রাফের কিছু বেসিক অ্যালগোরিদম জানা এবং সাথে সাথে মজার কিছু প্রবলেম দেখা। সব সংজ্ঞা একসাথে দেখলে মাথায় থাকবেনা, তাই একদম না জানলেই নয় সেরকম কিছু সংজ্ঞা প্রথমে দেখবো, এরপর প্রয়োজনমতো আরো কিছু সংজ্ঞা জেনে নিবো।

গ্রাফ কি?

ধরা যাক ৬টি শহরকে আমরা ১,২,৩,৪,৫,৬ দিয়ে চিহ্নিত করলাম। এবার যে শহর থেকে যে শহরে সরাসরি রাস্তা আছে তাদের মধ্যে লাইন টেনে দিলাম:

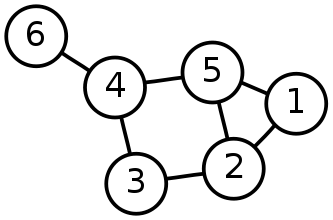
শহরগুলোর নাম ১,২ ইত্যাদি দিয়ে দিতে হবে এমন কোন কথা নেই, তুমি চাইলে ঢাকা, চট্টগ্রাম ইত্যাদি দিতে পারো। এটা খুবই সাধারণ একটা গ্রাফ যেখানে কিছু শহরের মধ্যের রাস্তাগুলো দেখানো হয়েছে। গ্রাফ থিওরির ভাষায় শহরগুলোকে বলা হয় নোড(Node) বা ভারটেক্স(Vertex) আর রাস্তাগুলোকে বলা হয় এজ(Edge)। গ্রাফ হলো কিছু নোড আর কিছু এজ এর একটা কালেকশন।

গ্রাফে নোড দিয়ে অনেককিছু বুঝাতে পারে, কোন গ্রাফে হয়তো নোড দিয়ে শহর বুঝায়, কোন গ্রাফে এয়ারপোর্ট, কোন গ্রাফে আবার হয়তো দাবার বোর্ডের একটা ঘর বুঝাতে পারে! আর এজ দিয়ে বুঝায় নোডগুলোর মধ্যের সম্পর্ক। কোন গ্রাফে এজ দিয়ে দুটি শহরের দূরত্ব বুঝাতে পারে, কোন গ্রাফে এক এয়ারপোর্ট থেকে আরেক এয়ারপোর্টে যাবার সময় বুঝাতে পারে, আবার দাবার বোর্ডে একটা ঘরে ঘোড়া থাকলে সেই ঘর থেকে কোন ঘরে যাওয়া যায় সেটাও বুঝাতে পারে।

নিচের ছবিতে দাবার বোর্ডটাও একটা গ্রাফ। প্রতিটা ঘর একটা করে নোড। যে ঘরে ঘোড়া আছে সেখান থেকে এজগুলো দেখানো হয়েছে:

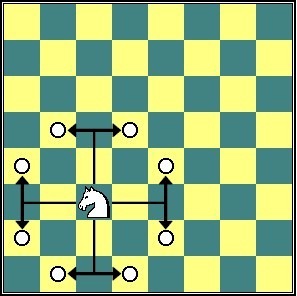
এককথায় নোডের কাজ কোন একধরণের অবজেক্টকে রিপ্রেজেন্ট করা আর এজ এর কাজ হলো দুটি অবজেক্টের মধ্যে সম্পর্কটা দেখানো।

অ্যাডজেসেন্ট নোড:
A নোড থেকে B নোডে একটা এজ থাকলে B কে বলা হয় A এর অ্যাডজেসেন্ট নোড। সোজা কথায় অ্যাডজেসেন্ট নোড হলো এজ দিয়ে সরাসরি কানেক্টেড নোড। একটা নোডের অনেকগুলো অ্যাডজেসেন্ট নোড থাকতে পারে।

ডিরেক্টেড গ্রাফ আর আনডিরেক্টেড গ্রাফ:
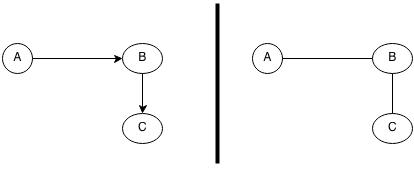
ডিরেক্টেড গ্রাফে এজগুলোতে তীরচিহ্ন থাকে, তারমানে এজগুলো হলো একমুখি(Unidirectional), আনডিরেক্টেড গ্রাফে এজগুলো দ্বিমুখী(Bidirectional)। নিচের ছবি দেখলেই পরিষ্কার হবে:

বামের ছবির গ্রাফ ডিরেক্টেড, ডানেরটা আনডিরেক্টেড।

ওয়েটেড আর আনওয়েটেড গ্রাফ:
অনেক সময় গ্রাফে এজগুলোর পাশে ছোট করে ওয়েট(Weight) বা কস্ট(Cost) লেখা থাকতে পারে:

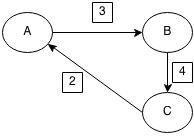
এই ওয়েট বা কস্ট দিয়ে অনেককিছু বুঝাতে পারে, যেমন দুটি শহরের দূরত্ব কত কিলোমিটার, অথবা রাস্তাটি দিয়ে যেতে কত সময় লাগে, অথবা রাস্তা দিয়ে কয়টা গাড়ি একসাথে যেতে পারে ইত্যাদি। আগের গ্রাফগুলো ছিলো আনওয়েটেড, সেক্ষেত্রে আমরা ধরে নেই সবগুলো এজের ওয়েটের মান এক(১)। সবগুলো ওয়েট ১ হলে আলাদা করে লেখা দরকার হয়না।

পাথ:
পাথ(Path) হলো যে এজগুলো ধরে একটা নোড থেকে আরেকটা নোডে যাওয়া যায়। অর্থাৎ এজের একটা সিকোয়েন্স।

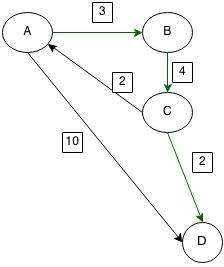
এক নোড থেকে আরেক নোডে যাবার অনেকগুলো পাথ থাকতে পারে। ছবিতে A থেকে D তে যাবার দুইটা পাথ আছে। A->B,B->C,C->D হলো একটা পাথ, এই পাথের মোট ওয়েট হলো ৩+৪+২=৯। আবার A->D ও একটা পাথ হতে পারে যেই পাথের মোট কস্ট ১০। যে পাথের কস্ট সবথেকে কম সেটাকে শর্টেস্ট পাথ বলে।

ডিগ্রী:

ডিরেক্টেড গ্রাফে একটা নোডে কয়টা এজ প্রবেশ করেছে তাকে ইনডিগ্রী, আর কোন নোড থেকে কয়টা এজ বের হয়েছে তাকে আউটডিগ্রী বলে। ছবিতে প্রতিটা নোডের ইনডিগ্রী আর আউটডিগ্রী দেখানো হয়েছে:

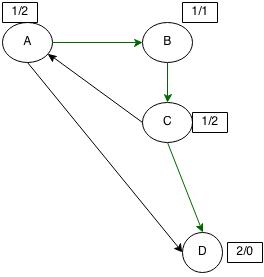
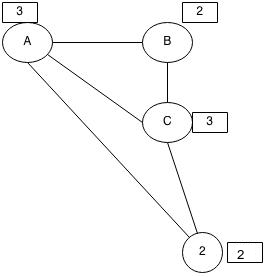
আনডিরেক্টেড গ্রাফে ইন বা আউটডিগ্রী আলাদা করা হয়না। একটা নোডের যতগুলো অ্যাডজেসেন্ট নোড আছে সেই সংখ্যাটাই নোডটার ডিগ্রী।

হ্যান্ডশেকিং লেমা একটা জিনিস আছে যেটা বলে একটা বিজোড় ডিগ্রীর নোডের সংখ্যা সবসময় জোড় হয়। উপরের গ্রাফে A আর C এর ডিগ্রী ৩, এরা বিজোড় ডিগ্রীর নোড। তাহলে বিজোড় ডিগ্রীর নোড আছে ২টা, ২ হলো একটা জোড় সংখ্যা। হ্যান্ডশেক করতে সবসময় ২টা হাত লাগে, ঠিক সেরকম একটা এজ সবসময় ২টা নোডকে যোগ করে। তুমি একটু চিন্তা করে দেখো:

২টা জোড় ডিগ্রীর নোডকে এজ দিয়ে যোগ করলে ২টা নতুন বিজোড় ডিগ্রীর নোড তৈরি হয়।

২টা বিজোড় ডিগ্রীর নোডকে এজ দিয়ে যোগ করলে ২টা বিজোড় ডিগ্রীর নোড কমে যায়।

১টা জোড় আর একটা বিজোড় ডিগ্রীর নোড যোগ করলে মোট বিজোড় ডিগ্রীর নোড সমান থাকে(এক পাশে কমে, আরেক পাশে বাড়ে)।

তাহলে দেখা যাচ্ছে হয় ২টা করে বাড়তেসে বা ২টা করে কমতেসে বা সমান থাকছে, তাই বিজোর ডিগ্রীর নোডের সংখ্যা সবসময় জোড়।

একইভাবে এটাও দেখানো যায় একটা গ্রাফের ডিগ্রীগুলোর যোগফল হবে এজসংখ্যার দ্বিগুণ। উপরের গ্রাফে ডিগ্রীগুলোর যোগফল ১০, আর এজসংখ্যা ৫।

এগুলো গেল একেবারেই প্রাথমিক কথাবার্তা। পরবর্তি লেখায় তুমি জানতে পারবে কিভাবে ভ্যারিয়েবলে গ্রাফ স্টোর করতে হয়। আশা করি গ্রাফ থিওরীতে তোমার যাত্রাটা দারুণ আনন্দের হবে, অনেক কিছু শিখতে পারবে।

অন্যান্য পর্ব