তুমি হয়তো এরকম প্রবলেম কনটেস্টে দেখেছ, একটি ইন্টিজার অ্যারে দেয়া আছে আর অনেকগুলো কুয়েরি দেয়া আছে। প্রতিটা কুয়েরিতে বলেছে একটা রেঞ্জের মধ্যে সবগুলো সংখ্যার যোগফল বলতে। অ্যারের সাইজ ১০^৫, কুয়েরির সংখ্যাও ১০^৫! বুঝতেই পারছো প্রতি কুয়েরিতে লুপ চালিয়ে যোগফল বের করতে পারবেনা। কিভাবে প্রবলেমটি সলভ করবে?
এটা সলিউশন খুব সহজ, তোমাকে কিউমুলেটিভ সাম রাখতে হবে। ধরো একটি অ্যারে আছে sum[MAX], তাহলে sum[i] তে রাখবে ১ থেকে i নম্বর ইনডেক্স পর্যন্ত সবগুলো সংখ্যার যোগফল। i থেকে j পর্যন্ত যোগফল বের করতে দিলে(i<=j) sum[j]-sum[i-1] হবে তোমার উত্তর। বুঝতে না পারলে নিচের উদাহরণটা দেখো:
ইনপুট:
arr[]={4, -9, 3, 7, 1, 0, 2}cumulative sum বের করবো:
sum[0]=0;
(for i=1;i<=n;i++) sum[i]=sum[i-1]+arr[i];তাহলে cumulative sum হবে:
sum[] ={4, -5, -2, 5, 6, 6, 8}
এটা একদম বাচ্চাদের কাজ, তুমি ৫মিনিটে কোড করে ফেলতে পারবে। কিন্তু প্রবলেমসেটার তোমাকে বিপদে ফেলতে বললো কুয়েরির করার মাঝে মাঝে অ্যারেটি বদলে দেয়া হবে!! মাঝে মাঝে তোমাকে বলবে i-তম ইনডেক্সের সংখ্যাটিকে x বানিয়ে দিতে, আবার আগের মতো যোগফলও বলতে বলবে। এখন কি করবে?
এবার আর কিউমুলেটিভ সাম দিয়ে কাজ হবেনা, তোমার দরকার হবে সেগমেন্ট ট্রি নামের একটা ডাটা স্ট্রাকচার। ইউনিভার্সিটিতে ডাটা স্ট্রাকচার কোর্সে তোমাকে এটা পড়াবেনা, কিন্তু এটা ব্যবহার করে অনেক কাজ করা যায়।
পরের অংশে যাবার আগে তোমার কিছু জিনিস সম্পর্কে ধারণা পরিষ্কার থাকতে হবে। রিকার্শন সম্পর্কে কোনো রকম অস্পষ্টতা থাকলে আপাতত সামনে না আগানোই ভালো। এছাড়া তুমি যদি মার্জ সর্ট সম্পর্কে জানো তাহলে সেগমেন্ট্রি বোঝা তোমার জন্য খুব সহজ হয়ে যাবে। এছাড়া ট্রি সম্পর্কে যদি কিছুই না জানো তাহলে সেগমেন্ট ট্রি এখনই শেখা কি ঠিক হবে? ঠিক মার্জ সর্টের মতো সেগমেন্ট্রি ট্রিও “ডিভাইড এন্ড কনকোয়ার” পদ্ধতিতে কাজ করে।
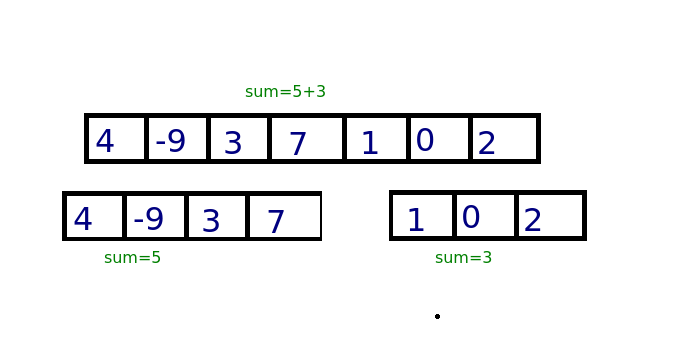
ডিভাইড এন্ড কনকোয়ার পদ্ধতির মূল কথা হলো একটা প্রবলেমকে ভেঙে ছোটো ছোটো অংশ বানাও, আগে সেই ছোট অংশ সলভ করো এবং ছোটো অংশের সলিউশন থেকে বড় অংশের সলিউশন বের করো। আমরা তাই অ্যারেটাকে ২টা অংশে ভাগ করে ফেলবো এবং দুইটা ভাগের যোগফল আলাদা করে বের করবো।
তুমি যদি বাম আর ডান পাশের ভাগের যোগফল আলাদা করে বের করতে পারো তাহলে খুব সহজেই বড় অংশটার যোগফল বের করতে পারবে। আমি বলার আগেই বুঝতে পারছো এরপরে কি করবো। ছোটো অ্যারেগুলোকে আরো টুকরা করবো যতক্ষণনা ১ সাইজের টুকরা পাই। ১ সাইজের টুকরোর যোগফল আমরা জানি, সেখান থেকে বড়গুলোর যোগফল বের করে ফেলবো।
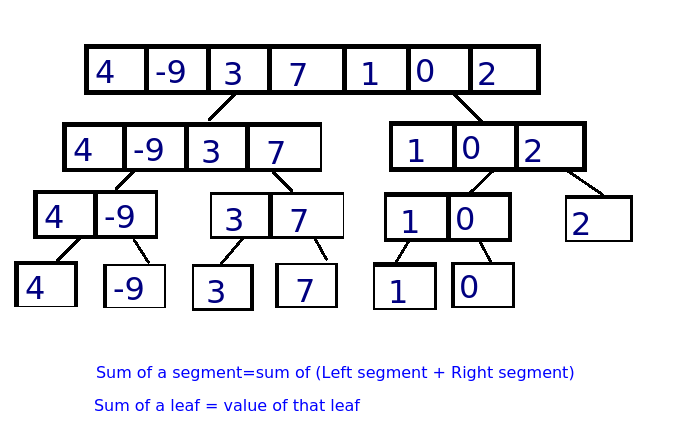
ছবিটা দেখতে বিদঘুটে হলেও জিনিসটা খুবই সহজ। আমরা অ্যারেটাকে ভাঙতে ভাঙতে ছোট করে ফেলেছি, সবথেকে ছোট অংশের(লিফ নোড) যোগফল আমরা জানি, সেখান থেকে বড় গুলো সহজেই বের করতে পারবো বাম এবং ডানের অংশ যোগ করে।
ছবিটায় প্রতিটা সেগমেন্টকে যদি একটা নোড ধরি তাহলে একটা ট্রি তৈরি হয়ে গিয়েছে, প্রতিটা নোডে আছে একটা অংশ বা রেঞ্জের যোগফল। এটার নামই সেগমেন্ট ট্রি। এখন তোমার মনে হতে পারে এই জিনিস দিয়ে কিভাবে i থেকে j অংশের যোগফল বের করবে কারণ আমরাতো ভাঙছি সম্পূর্ণ অ্যারেটা আর সবশেষে পাচ্ছি সবটুকুর যোগফল। কিছুক্ষণের মধ্যে এটার উত্তর পাবে। আমরা ট্রি টাকে একটু অন্যভাবে দেখি:
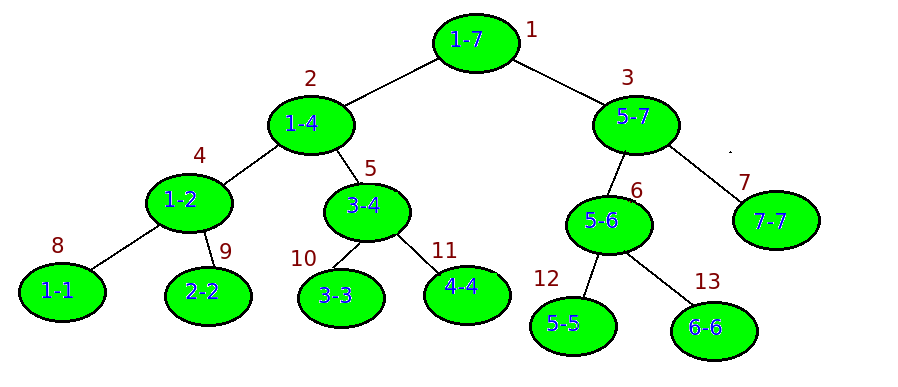
খেয়াল করে দেখো আগের ট্রি টাই একেছি কিন্তু এবার সেগমেন্টগুলো পুরোটা না দেখিয়ে শুধু রেঞ্জটা লিখেছি। যেমন ৩ নম্বর নোডে আছে ৫ থেকে ৭ ইনডেক্সের সবগুলোর যোগফল। নোডের নাম্বারিং টা গুরুত্বপূর্ণ। রুট নোড হবে ১, তার বামের নোড হবে ১*২=২, এবং ডানের নোড হবে (১*২+১)=৩। অর্থাৎ রুট x হলে বামেরটা হবে 2x এবং ডানেরটা 2x+1। বাইনারি ট্রি অ্যারেতে স্টোর করার জন্য সুবিধাজনক পদ্ধতি এটা।
এখন আগে দেখি কিভাবে এই স্ট্রাকচারটা তৈরি করবো। নিচের কোডটি দেখো, ব্যাখ্যা আছে কোডের নিচে:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
#define mx 100001 int arr[mx]; int tree[mx * 3]; void init(int node, int b, int e) { if (b == e) { tree[node] = arr[b]; return; } int Left = node * 2; int Right = node * 2 + 1; int mid = (b + e) / 2; init(Left, b, mid); init(Right, mid + 1, e); tree[node] = tree[Left] + tree[Right]; } int main() { //READ("in"); int n; cin >> n repl(i, n) cin >> arr[i]; init(1, 1, n); return 0; } |
tree[] অ্যারেতে আমরা ট্রি টাকে স্টোর করবো। ট্রি অ্যারের সাইজ হবে ইনপুট অ্যারের ৩গুণ(কেন??)। init ফাংশনটি arr অ্যারে থেকে ট্রি তৈরি করে দিবে। init এর প্যারামিটার হলো node,b,e, এখানে node=বর্তমানে কোন নোডে আছি এবং b,e হলো বর্তমানে কোন রেঞ্জে আছি। শুরুতে আমরা নোড ১ এ থাকবো এবং ১-৭ রেঞ্জে থাকবো(ট্রি এর ছবিটা দেখো)।
যদি (b==e) হয়ে যায় তাহলে আমরা শেষ নোডে পৌছে গেছি, এখানে যোগফল হবে অ্যারেতে যে ভ্যালু আছে সেটাই, সেটাকে ট্রিতে স্টোর করে রিটার্ণ করে দিলাম। যদি (b==e) না হয় তাহলে অ্যারেটা কে দুই ভাগে ভাগ করতে হবে। বাম পাশের নোডের ইনডেক্স হবে node*2 এবং ডান পাশেরটা node*2+1। এবং অ্যারেটাকে ভাঙবো ঠিক মাঝখানে। এবার রিকার্সিভলি দুই পাশে init কল করলে বাম এবং ডান পাশের ছোটো অংশের যোগফল বের হয়ে যাবে। দুইপাশের কাজ শেষ হয়ে গেলে বর্তমান নোডের যোগফল হবে বাম এবং ডানের নোডের যোগফল।
বুঝতে সমস্যা হলে কোডটা হাতে-কলমে একবার সিমুলেট করো, তাহলেই পরিষ্কার হয়ে যাবে।
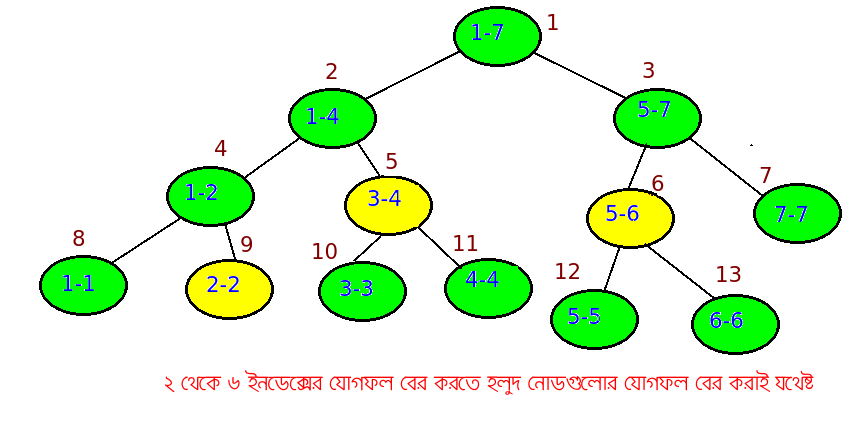
এইবার আমাদের একটা কুয়েরি ফাংশন দরকার যেটা i থেকে j এর মধ্যে সবগুলো সংখ্যার যোগফল বলে দিবে। ধরো i=2 এবং j=6। তাহলে লক্ষ্য করো নিচের হলুদ রঙের নোডগুলোর যোগফলই তোমার উত্তর:
2-6 রেঞ্জের জন্য হলুদ নোডগুলো আমাদের রিলেভেন্ট নোড, বাকিগুলো এক্সট্রা। আমাদের কুয়েরি ফাংশনের কাজ হবে শুধু রিলেভেন্ট নোডগুলোর যোগফল বের করা। কোডটা init ফাংশনের মতোই হবে তবে কিছু কন্ডিশন অ্যাড করতে হবে। ধরো তুমি এমন একটা নোডে আছো যেখানে b-e রেঞ্জের যোগফল আছে। তুমি এই নোডটা রিলেভেন্ট কিনা সেটা কিভাবে বুঝবে? এখানে ৩ধরণের ঘটনা ঘটতে পারে:
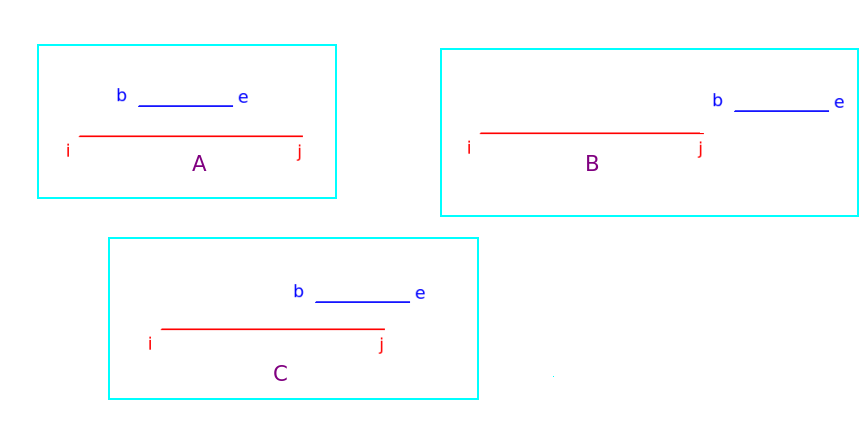
কেস A: (b >= i && e <= j) এরকম হলে কারেন্ট সেগমেন্টটা পুরোটাই i-j এর ভিতরে আছে, সেগমেন্টটা রিলেভেন্ট।
কেস B: (i > e || j < b) এরকম হলে কারেন্ট সেগমেন্টটা পুরোটাই i-j এর বাইরে আছে, এই সেগমেন্টটা নেয়ার দরকার নাই।
কেস C: কেস A,B সত্য না হলে এই সেগমেন্টের কিছু অংশ i-j এর মধ্যে, সেগমেন্টটাকে আরো ভেঙে নিচে গিয়ে রিলেভেন্ট অংশটা নিতে হবে।
তাহলে আমরা কুয়েরি ফাংশনে প্রতি নোডে গিয়ে দেখবো সেগমেন্টটা রিলেভেন্ট নাকি। যদি রিলেভেন্ট হয় তাহলে সেই নোডের যোগফল রিটার্ণ করবো, যদি বাইরে চলে যায় তাহলে ০ রিটার্ণ করে দিবো, অন্যথায় আমরা সেগমেন্টটা আরো ভেঙে রিলেভেন্ট অংশ খুজবো।
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
int query(int node, int b, int e, int i, int j) { if (i > e || j < b) return 0; //বাইরে চলে গিয়েছে if (b >= i && e <= j) return tree[node]; //রিলেভেন্ট সেগমেন্ট int Left = node * 2; //আরো ভাঙতে হবে int Right = node * 2 + 1; int mid = (b + e) / 2; int p1 = query(Left, b, mid, i, j); int p2 = query(Right, mid + 1, e, i, j); return p1 + p2; //বাম এবং ডান পাশের যোগফল } |
init ফাংশনের মতোই কাজ করে কুয়েরি ফাংশনটা। i,j হলো যে রেঞ্জের যোগফল বের করতে হবে সেটা আর b,e হলো কারেন্ট নোডে যে রেঞ্জের যোগফল আছে সেটা।
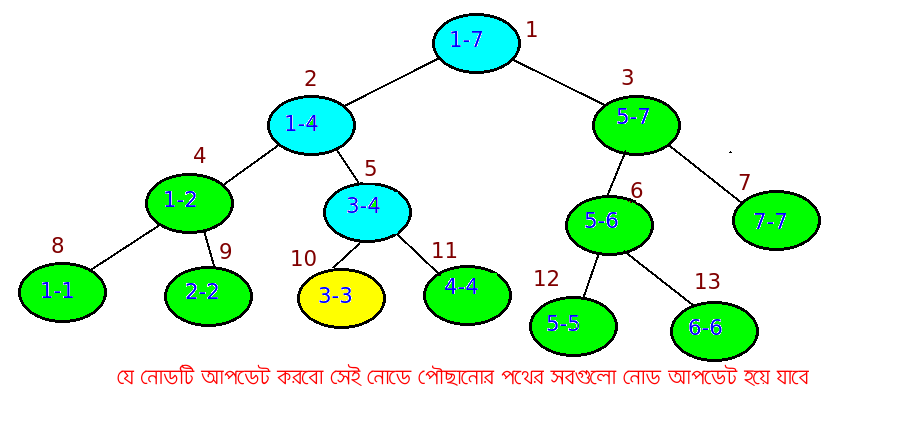
সবশেষে আপডেট করা, যার জন্য কিউমুলিটিভ সাম ব্যবহার না করে ট্রি বানিয়েছি। তোমাকে বললো i=৩ নম্বর ইনডেক্সের ভ্যালু x=১০ করে দিতে। তারমানে ট্রি তে যেই নোডে ৩-৩ রেঞ্জের যোগফল আছে সেটা আপডেট করে দিবো(নিচের ছবির হলুদ নোড)। নোডটির ভ্যালু আপডেট হলে পথে যেসব নোড ছিলো(নীল নোড) সবগুলোর যোগফল বদলে যাবে, বাকি নোডগুলোর কোনো পরিবর্তন হবেনা কারণ ৩ নম্বর নোড সেগুলো রেঞ্জের বাইরে।
আপডেটের কোডেও খুব বেশি পার্থক্য নেই:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
void update(int node, int b, int e, int i, int newvalue) { if (i > e || i < b) return; //বাইরে চলে গিয়েছে if (b >= i && e <= i) { //রিলেভেন্ট সেগমেন্ট tree[node] = newvalue; //নতুন মান বসিয়ে দিলাম return; } int Left = node * 2; //আরো ভাঙতে হবে int Right = node * 2 + 1; int mid = (b + e) / 2; update(Left, b, mid, i, newvalue); update(Right, mid + 1, e, i, newvalue); tree[node] = tree[Left] + tree[Right]; } |
i নম্বর ইনডেক্সে আপডেট করবো, এক্সট্রা সেগমেন্টগুলো শুরুতেই বাদ দিয়ে দিয়েছি। রিলেভেন্ট সেগমেন্টে গেলে নতুন মান বসিয়ে দিয়েছি, এইখানে কন্ডিশনটা if(b==e) লিখলেও চলতো কারণ সবসময় লিফ নোডে আপডেট করছি আমরা।
সেগমেন্ট ট্রি তো মোটামুটি এই ৩টা ফাংশন সবসময় থাকে init,query,update। অনেক সময় init এর কাজটা আপডেট দিয়ে করে ফেলা যায়। যেমন এখানে তুমি init কল করে ট্রি না বানিয়ে প্রতিটা নোড আলাদা করে আপডেট করে ট্রি বানাতে পারতে। ৩টা ফাংশন মিলিয়ে কোডটা হবে:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
#define mx 100001 int arr[mx]; int tree[mx * 3]; void init(int node, int b, int e) { if (b == e) { tree[node] = arr[b]; return; } int Left = node * 2; int Right = node * 2 + 1; int mid = (b + e) / 2; init(Left, b, mid); init(Right, mid + 1, e); tree[node] = tree[Left] + tree[Right]; } int query(int node, int b, int e, int i, int j) { if (i > e || j < b) return 0; //বাইরে চলে গিয়েছে if (b >= i && e <= j) return tree[node]; //রিলেভেন্ট সেগমেন্ট int Left = node * 2; //আরো ভাঙতে হবে int Right = node * 2 + 1; int mid = (b + e) / 2; int p1 = query(Left, b, mid, i, j); int p2 = query(Right, mid + 1, e, i, j); return p1 + p2; //বাম এবং ডান পাশের যোগফল } void update(int node, int b, int e, int i, int newvalue) { if (i > e || i < b) return; //বাইরে চলে গিয়েছে if (b >= i && e <= i) { //রিলেভেন্ট সেগমেন্ট tree[node] = newvalue; return; } int Left = node * 2; //আরো ভাঙতে হবে int Right = node * 2 + 1; int mid = (b + e) / 2; update(Left, b, mid, i, newvalue); update(Right, mid + 1, e, i, newvalue); tree[node] = tree[Left] + tree[Right]; } int main() { READ("in"); int n; cin >> n; repl(i, n) cin >> arr[i]; init(1, 1, n); update(1, 1, n, 2, 0); cout << query(1, 1, n, 1, 3) << endl; update(1, 1, n, 2, 2); cout << query(1, 1, n, 2, 2) << endl; return 0; } |
সেগমেন্ট ট্রি অ্যারেকে বারবার ২ভাগে ভাগ করে, ট্রি এর গভীরতা হবে সর্বোচ্চ log(n) তাই প্রতিটা কুয়েরি আর আপডেটের কমপ্লেক্সিটি O(logn)। init ফাংশনে ট্রি এর প্রতিটা নোডেই একবার যেতে হয়েছে তাই সেক্ষেত্রে কমপ্লেক্সিটি হবে প্রায় O(nlogn)।
সেগমেন্ট ট্রি তুমি তখনই ব্যবহার করতে পারবে যখন দুইটা ছোটো সেগমেন্টকে একসাথে করে বড় সেগমেন্টের ফলাফল বের করা যায়। যোগফল ছাড়াও একটা রেঞ্জের মধ্যে সর্বোচ্চ বা সর্বনিম্ন মান তুমি বের করতে পারবে, বামপাশের সর্বোচ্চ মান এবং ডানপাশের সর্বোচ্চ মান জানলে রুট নোডেরটাও বের করা যায় খুবই সহজে।
এখানে একটা গুরুত্বপূর্ণ জিনিস বাদ পড়েছে। ধরো তোমাকে একটা ইনডেক্সে আপডেট করতে না বলে i থেকে j ইনডেক্সে আপডেট করতে বললো, তাহলে কি করবে? প্রতিটা লিফ নোডে আলাদা করে আপডেট করলে O(nlogn) হয়ে যাবে কমপ্লেক্সিটি যেটা TLE দিবে। এটার জন্য খুবই এলিগেন্ট একটা টেকনিট আছে যার নামে অলস(লেজি) প্রপাগেশন! সে সম্পর্কে পরের পর্বে জানবো, এখন তুমি যতটুকু শিখেছো সেটা দিয়ে array queries(lightoj), Multiple of 3 (SPOJ), Frequent Values (UVA), Curious Robin Hood(lighoj) প্রবলেমটা সলভ করো।
ফেসবুকে মন্তব্য
Powered by Facebook Comments


খুব ভালো লিখেছেন।
This is Straightforward
ধন্যবাদ, অ্যাড করে দিলাম লেখাতে।
ট্রি অ্যারের সাইজ হবে ইনপুট অ্যারের ৩গুণ(কেন??)।
query function seems to me inefficient…..in array queries প্রবলেম it will give tle…..a little modification gives faster solution ………
int query(int node,int b,int e,int i,int j)
{
if (i > e || j = i && e <= j) return tree[node]; //????????? ????????
int Left=node*2; //???? ????? ???
int Right=node*2+1;
int mid=(b+e)/2;
if(j mid)
{
return query(right,mid+1,end,i,j);
}
else return query(Left,b,mid,i,mid)+query(Right,mid+1,e,mid+1,j); //??? ??? ??? ????? ??????
}
না টিএলই দিবেনা, logn এ কাজ করবে এটা, এক্সট্রা সব সেগমেন্ট ফেলে দিবে।
ট্রি অ্যারের সাইজ হবে ইনপুট অ্যারের ৩গুণ………….কেন….???
I think that tree size is double of input array size and double is enough.But why triple????????
ট্রি তে নোড থাকবে দ্বিগুণ সেটা ঠিক আছে কিন্তু অ্যারে সাইজ আরো বেশি নিতে হবে, দ্বিগুণ যথেষ্ট না। ১০০০০০ নোডের একটা সেগমেন্ট ট্রি বানিয়ে init ফাংশন কল করে দেখো “node” ভ্যারিয়েবলটার মান সর্বোচ্চ কত হয়, দেখবে আড়াই গুণের একটু বেশি হয়েছে। এমনকি ৩ গুণও যথেষ্ট না যদি ৩০০০০০ টা নোড থাকে। এখানে একটা অ্যানালাইসিস আছে: http://wcipeg.com/wiki/Segment_tree#Analysis।
vaiya i am a java coder but i got memory limit exceeded i dont know what to do?? Please help me.. 🙁
import java.io.*;
import java.util.*;
class SegmentTree{
public int [] tree;
public int [] array;
public int sum = 0;
public SegmentTree(int [] y){
tree = new int[y.length*3];
array = y;
}
public void init(int node,int start,int end)
{
if(start==end)
{
tree[node]= array[start];
return;
}
else{
int Left=node*2;
int Right=Left+1;
int mid=(start+end)/2;
init(Left,start,mid);
init(Right,mid+1,end);
tree[node]=Math.min(tree[Left],tree[Right]);
}
}
public int query(int node,int start,int end,int i,int j)
{
if(start end || j = i && end 0){
k.readLine();
StringTokenizer s = new StringTokenizer(k.readLine());
int N = Integer.valueOf(s.nextToken());
int [] y = new int[N];
int q = Integer.valueOf(s.nextToken());
StringTokenizer ss = new StringTokenizer(k.readLine());
int c = 0;
while(ss.hasMoreTokens()){
y
= Integer.valueOf(ss.nextToken());
}
SegmentTree a = new SegmentTree(y);
a.init(1,0,y.length-1);
z.println("Case "+(test++));
while(q-->0){
StringTokenizer sss = new StringTokenizer(k.readLine());
int i = Integer.valueOf(sss.nextToken());
int j = Integer.valueOf(sss.nextToken());
i--;
j--;
z.println(a.query(1,0,y.length-1, i, j));
}
}
z.flush();
}
}
Sorry to mention thsi problem is from Light oz 1082(Array Queries)
মেমরী খুব সম্ভবত 2 * 2^([logN] + 1) লাগে ৩ গুন না।
“অর্থাৎ রুট x হলে বামেরটা হবে 2x এবং ডানেরটা 2x*1”
এখানে ডানেরটা 2*x+1 হতে পারে ।
“ARRAY QUIERIES” can be nicely solved just by using SHAFAET BHAI’s concept described here 🙂
বাইনারি ইন্ডেক্সড ট্রি এর উপর টিউটোরিয়াল দেওয়া যায় ভাইয়া, প্লিইইজ?
দিলাম, প্রথম পাতায় দেখ!
ভাইয়া প্রথম লাইনে বলসেন “একটি ইন্টিজার অ্যারে দেয়া আছে আর অনেকগুলো কুয়েরি দেয়া আছে। ” কুয়েরি কি জিনিশ?
রুট x হলে বামেরটা হবে 2x এবং ডানেরটা 2x*1 এটা টাইপিং মিসটেক হয়েছে সম্ভবত। ডানেরটা 2x+1 হবে।
ঠিক করে দিলাম, ধন্যবাদ।
@নোমান
কুয়েরি হল প্রশ্নটাই অর্থাত যা চাওয়া হয়েছে। যেমন অ্যরেতে একটা রেঞ্জ এর যোগফল চাওয়া হয়েছে। এটি একটি কুয়েরি।
২ থেকে ৫ ইনডেক্স পর্যন্ত যোগফল কত?
৩ থেকে ৬ ইনডেক্স পর্যন্ত যোগফল কত?
১ থেকে ৭ ইনডেক্স পর্যন্ত যোগফল কত?
এগুলোই হল কুয়েরি।
😀
I hope this will help.
সেগমেন্ট ট্রি ব্যবহার করে কি একটা রেঞ্জের মধ্যে গসাগু বের করা যাবে?? করা গেলে তখন কুয়েরি ফাংশন এ রিলিভেন্ট নোডের বাইরে চলে গেলে কি রিটার্ন করতে হবে
এটার উত্তর আমার জানা নেই, দু:খিত।
Vaiya…..
init ফাংশনে ট্রি এর প্রতিটা নোডেই একবার যেতে হয়েছে তাই সেক্ষেত্রে কমপ্লেক্সিটি হবে প্রায় O(nlogn)।
But tree te to at most 2*n ta node thakbe ………
tahole to complexity O(n) hbe…….
O(nlogn) kivabe…………
2*n টা নোড থাকবে এই কথাটা ভুল!
if (b >= i && e =i&&e<=i) for single update instead of
if(b==i&&e==i)
why if(b>=i&&e<=i) instead of if(b==i&&e==i) ?
“”সেগমেন্ট ট্রি তুমি তখনই ব্যবহার করতে পারবে যখন দুইটা ছোটো সেগমেন্টকে একসাথে করে বড় সেগমেন্টের ফলাফল বের করা যায়। যোগফল ছাড়াও একটা রেঞ্জের মধ্যে সর্বোচ্চ বা সর্বনিম্ন মান তুমি বের করতে পারবে, বামপাশের সর্বোচ্চ মান এবং ডানপাশের সর্বোচ্চ মান জানলে রুট নোডেরটাও বের করা যায় খুবই সহজে।””
.
.
.
ভাইয়া,
একটা রেঞ্জের মধ্যে সর্বোচ্চ বা সবনিম্ন মান বের করতে সেগমেন্ট ট্রি ছাড়া কি ধরণের Problem হতে পারে ? আর minimum / maximum বের করার জন্য segment tree এর কোন property টা ব্যবহার করতে হবে ?
solved !!! thanks for the tutorial vaia
ভাইয়া, update এর কোডটার ৪ নাম্বার লাইনটা একটু কেমন জানি। equality চেক করলে বেশি ভাল হয় না?
array queries এ কারো যদি TLE আসে তাহলে scanf & printf ব্যবহার করে দেখতে পার । আমি এভাবে AC পাইছি 😀
ট্রি অ্যারের সাইজ হবে ইনপুট অ্যারের ৩গুণ কেন??
কোন রেঞ্জে e >= b হবেই , তাই b >= i && e <= i (update এর ৫ নং লাইন ) তখনই সম্ভব যখন e == b == i হবে |
ভাইয়া, SPOJ – Multiples of 3 এই প্রবলেমটা কি লেজি প্রোপাগেশন ছাড়া করা সম্ভব? এখানে তো একটা রেঞ্জের জন্য ভ্যালু আপডেট করতে হচ্ছে।