আমরা যখন প্রবলেম সলভ করতে করতে মাথার চুল ছিড়ে ফেলি তখন প্রায়ই এমন কিছু প্রবলেম সামনে আসে যেগুলো সলভ করতে গেলে সবথেকে শক্তিশালী কম্পিউটারও হাজার হাজার বছর লাগিয়ে দিবে। বড় বড় কম্পিউটার বিজ্ঞানীরা যখন দিন-রাত চিন্তা করেও এগুলো সলভ করতে পারলেননা তখন তারা এই প্রবলেমগুলোকে কিছু ক্যাটাগরিতে ফেলে দিয়ে বললেন “এই ক্যাটাগরির প্রবলেমগুলো সলভ করার সাধ্য এখনো আমাদের হয়নি, তোমরা কেও পারলে সলভ করে দিয়ে ১০ লক্ষ ডলার পুরস্কার নিয়ে যাও”। সেগুলোকেই আমরা NP-complete, NP-hard ইত্যাদি নামে চিনি।
NP ক্যাটাগরির প্রবলেমগুলো কম্পিউটার সায়েন্সে খুব বিখ্যাত। যেমন একটা গ্রাফে সবথেকে লম্বা পথ খুজে বের করা, ৩টা রঙ দিয়ে গ্রাফ কালারিং করা ইত্যাদি। এগুলোকে এখন পর্যন্ত কেও পলিনমিয়াল টাইমে সলভ করতে পারেনি, যেসব সলিউশন বের হয়েছে সেগুলো সামান্য বড় ইনপুটের জন্যই কাজ করেনা। মজার ব্যাপার হলো এই প্রবলেমগুলোর যেকোন একটা যদি তুমি সলভ করতে পারো তাহলে সবগুলো প্রবলেমই সলভ করা যাবে তোমার সলিউশনের সাহায্যে, অনেক বছর ধরে মানুষকে ভাবানো কঠিন সব প্রবলেম চোখের নিমেষে সলভ হয়ে যাবে একটা মাত্র সলিউশন দিয়ে, কম্পিউটার বিজ্ঞানের চেহারাটাই পাল্টে দিবে এটা। সেজন্যই এত বড় বড় পুরষ্কার ঘোষণা করা হয়েছে NP প্রবলেম সলভ করা জন্য।
এই আর্টিকেলটা পড়ার আগে তোমাকে অ্যালগোরিদম কমপ্লেক্সিটি নিয়ে জানতে হবে। এছাড়া NP নিয়ে জানতে হলে আমাদের প্রথমে কয়েকটা টপিক নিয়ে কিছুটা জানতে হবে, আগে সেটা নিয়ে আলোচনা করবো। এই লেখাটা পড়ার পর তুমি P-NP, টুরিং মেশিন নিয়ে একটা ভালো ধারণা পাবে।
টুরিং মেশিন
১৯৩৬ সালে এলান টুরিং একটা “হাইপোথেটিকাল” মেশিন ডিজাইন করেন, বাস্তবে তৈরি করেননি, শুধুই থিওরি দিয়েছেন। মেশিনটা অ্যালগোরিদম সিমুলেট করতে পারে। এই মেশিন দিয়ে ব্যাখ্যা করা যায় কিভাবে কম্পিউটার একটা প্রবলেম সলভ করতে পারে। টুরিং চিন্তা করতেন “একটা প্রবলেম কম্পিউটেবল” বলতে কি বোঝায়? একটা প্রবলেম “কম্পিউটেবল” মানে হলো “কিছু ইনস্ট্রাকশন থাকবে যেগুলো একটা কম্পিউটার ফলো করলে একটা কাজ শেষ হবে”, এই ইনস্ট্রাকশনগুলোই হলো অ্যালগোরিদম। ইনস্ট্রাকশনগুলো কম্পিউটার ফলো করতে পারবে নাকি সেটা নির্ভর করে মেশিনের সামর্থের উপর। যেসব অ্যালগোরিদম টুরিং মেশিন দিয়ে সলভ করা যায় সেগুলো “টুরিং-কম্পুউটেবল”।
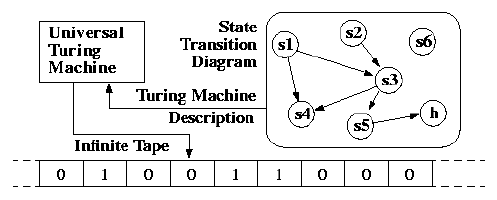
টুরিং মেশিনে একটা অসীম লম্বা টেপ থাকে(নিচের ছবি)। একটা হেড টেপের কোনো জায়গায় পয়েন্ট করে প্রবলেমের একটা “স্টেট” নির্দেশ করে। প্রতিটা স্টেট থেকে কোন স্টেট যাওয়া যায় সেটা নির্ভর করে ওই প্রবলেমের “ট্রানজিশন ডায়াগ্রাম” এর উপর। সহজ কথায় ডায়াগ্রামে বলা থাকে কোন ইনপুটের জন্য কোন স্টেট থেকে কোন স্টেটে যেতে হবে সেটা।
আধুনিক কম্পিউটারগুলো টুরিং মেশিন কম্পিউটেবল। টুরিং মেশিন দিয়ে সলভ করা না গেলে কম্পিউটার দিয়ে সলভ করা যায়না, তাই এটা নিয়ে আমাদের এত আগ্রহ।
নন-ডিটারমিনিস্টিক টুরিং মেশিন:
ধরো তোমার ইনস্ট্রাকশন সেটে বলা আছে “তুমি যদি একটা ১০ নম্বর স্টেটে থাকো এবং ইনপুটে একটা “A” পাও তাহলে বামে যাও” এবং একই সাথে বলা থাকে “তুমি যদি একটা ১০ নম্বর স্টেটে থাকো এবং ইনপুটে একটা “A” পাও তাহলে ডানে যাও” তাহলে তুমি কোনটা করবে? একই স্টেটে একই ইনপুটের জন্য ভিন্ন ইনস্ট্রাকশন! নন-ডিটারমিনিস্টিক টুরিং মেশিন এই ধরণের সিচুয়েশনে অনুমানের উপর নির্ভর করবে। সে রেন্ডমলি অনুমান করে কোনো একটা পাথে চলে যাবে।হয়তো সেই অনুমান ভুল এবং কম্পিউটেশনটা ভুল আউটকাম দেবে। কিন্তু এখানে বিবেচ্য হলো এমন কোনো সঠিক সিদ্ধান্তের সিকুয়েন্স আছে কি না। নন-ডিটারমিনিস্টিক মেশিন সবসময় ঠিক রেজাল্ট দিবে এমন কোনো কথা নেই, যদি রেজাল্ট পজিটিভ হয় তাহলে অবশ্যই সলিউশন আছে, কিন্তু নেগেটিভ হলেও নিশ্চিত করে বলা যায়না যে আসলে পজিটিভ রেজাল্ট আছে নাকি নেই। এজন্যই এধরণের মেশিনের নাম নন-ডিটারমিনিস্টিক।
ডিটারমিনিস্টিক টুরিং মেশিন: এই মেশিনের ইনস্ট্রাকশন সেটে এভাবে একই সাথে দুই রকম ইনস্ট্রাশন থাকবেনা। প্রতি সিচুয়েশনে নির্দিষ্ট কোনদিকে যেতে হবে সেটা আগে থেকে জানা থাকবে।
আধুনিক কম্পিউটার ডিটারমিনিস্টিক টুরিং মেশিন এর সমতুল্য। নন-ডিটারমিনিস্টিক ইনস্ট্রাকশন সেট নিয়ে কম্পিউটার কাজ করেনা।
পলিনমিয়াল কমপ্লেক্সিটি: যেসব প্রবলেমের কমপ্লেক্সিটি ইনপুট সাইজের পাওয়ার সেগুলো পলিনমিয়াল কমপ্লেক্সিটি, যেমন O(n),O(nlogn),O(n^3) ইত্যাদি।
P(Polynomial) প্রবলেম
P বা পলিনমিয়াল ক্যাটাগরি প্রবলেমকে ডিটারমিনিস্টিক টুরিং মেশিন দিয়ে পলিনমিয়াল টাইমে সলভ করা যায়। যেমন শর্টেস্ট পাথ প্রবলেম, ন্যাপস্যাক প্রবলেম। শুধু যে সেগুলো সলভ করা যায় সেটা না, একটা “সার্টিফিকেট” দিলে সেটা পলিনমিয়াল টাইমে ভেরিফাই ও করা যায়। সার্টিফিকেট কি? ধরা যাক ইউলার পাথ প্রবলেমের কথা, একটা গ্রাফের সবগুলো এজ ভিজিট করতে হবে এবং কোন এজ দুইবার ভিজিট করা যাবেনা। এখানে সার্টিফিকেট হলো কিছু এজ এর সিকোয়েন্স (e1,e2….,eK)। আমাদেরকে এই সিকোয়েন্স দিলে সহজেই বলতে পারবো এটা একটা ভ্যালিড পাথ নাকি। প্রতিটা নোড ধরে আগাবো, দেখবো এক নোড দুইবার ভিজিট হয়েছে নাকি এবং সবগুলো নোড ভিজিট হয়েছে নাকি। O(E) তেই আমরা এটা ভেরিফাই করতে পারবো যেখানে E হলো এজ সংখ্যা। P প্রবলেম পলিনমিয়াল টাইমে সলভ করা যায়, এবং একটা সলিউশন(সার্টিফিকেট) ভ্যালিড নাকি সেটা পলিনমিয়াল টাইমে ভেরিফাই করা যায়।
NP(Non-deterministic Polynomial) প্রবলেম
NP প্রবলেমকে ডিটারমিনিস্টিক টুরিং মেশিন দিয়ে পলিনমিয়াল টাইমে ভেরিফাই করা যায়। কিন্তু পলিনমিয়াল টাইমে সলভ করা যায় কি যায় না সেটা প্রমাণ করা সম্ভব হয়নি। যেমন হ্যামিল্টন পাথ প্রবলেম, একটা গ্রাফের সব নোড ভিজিট করতে হবে, একটা নোড দুইবার ভিজিট করা যাবেনা। তোমাকে যদি কিছু নোডের সিকুয়েন্স দেয় তুমি সহজেই ইউলার পাথ এর মতো করে ভেরিফাই করতে পারবে। কিন্তু একটা গ্রাফে হ্যামিল্টন পাথ আছে নাকি নাই কিভাবে বলবে? এটা বের করার জন্য পলিনমিয়াল অ্যালগোরিদম এখন পর্যন্ত আবিষ্কার হয়নি। পলিনমিয়াল অ্যালগোরিদম না থাকলে আমরা সলভ করি এক্সপোনেন্টসিয়াল অ্যালগোরিদম দিয়ে যেগুলোর কমপ্লেক্সিটি O(2^n),(k^n) এরকম। এই ধরণের কমপ্লেক্সিটি সাজেস্ট করে তোমাকে ব্রুট ফোর্সের সাহায্যে সবকরম পসিবিলিটি চেক করতে হবে, সাধারণত ব্যাকট্র্যাকিং দিয়ে এসব প্রবলেম সলভ করা হয়।
P=NP??
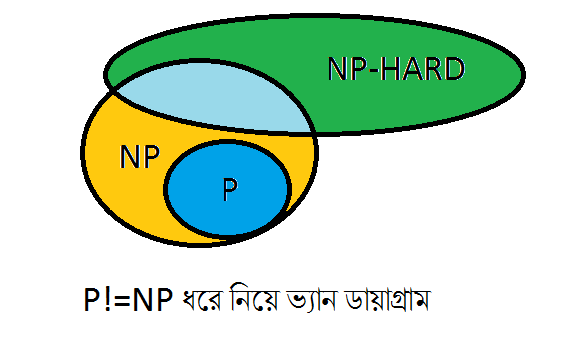
প্রতিটা P প্রবলেমেই NP প্রবলেম ক্যাটাগরিতে পরে। কারণ সব P প্রবলেমকে পলিনমিয়াল টাইমে ভেরিফাই করা যায় যেটা NP ক্যাটাগরির একমাত্র শর্ত। তারমানে P হলো NP এর একটা সাবসেট। কিন্তু সব NP প্রবলেমই কি P প্রবলেম? যেসব প্রবলেমের সার্টিফিকেট পলিনমিয়াল টাইমে ভেরিফাই করা যায় সেগুলোর সবগুলোকেই কি পলিনমিয়াল টাইমে সলভ করা যায়? হ্যামিল্টন পাথ, স্যাট প্রবলেম ইত্যাদির ক্ষেত্রে আমরা জানিনা প্রবলেমগুলো P তে ফেলা যায় নাকি। আমরা জানিনা P=NP নাকি P!=NP। এটা কম্পিউটার সায়েন্সের সবথেকে বিখ্যাত একটি ওপেন প্রবলেম। ক্লে ম্যাথমেটিকাল ইন্সটিটিউট এটাকে ৭টি মিলেনিয়াম প্রাইজ প্রবলেম এর একটি ধরে ১০ লক্ষ ডলারের প্রাইজমানি ঘোষণা করেছে! তবে কম্পিউটার বিজ্ঞানী এবং গণিতবিদরা ধারণা করে P!=NP, কিন্তু শুধুমাত্র ধারণা কখনোই বিজ্ঞান নয়, আইনস্টাইন মুখে কি ধারণার কথা বললেন সেটা বিজ্ঞান নয়, তিনি পিয়ার রিভিউড জার্নালে যেটা প্রকাশ করেছেন সেটা বিজ্ঞান!
NP hard: এই ক্যাটাগরির প্রবলেমগুলো “অন্তত NP প্রবলেমের মতো” কঠিন। এই কথার মানে কি আর কঠিনকে কিভাবে পরিমাপ করে? অনেক সময়ই একটা প্রবলেমকে অন্য প্রবলেমে কনভার্ট করা যায়। ধরা যাক A একটা প্রবলেম যেটা NP ক্যাটাগরির এবং B প্রবলেমটা আমরা সলভ করতে চাই। A প্রবলেমকে যদি আমরা পলিনমিয়াল টাইমে B প্রবলেমে কনভার্ট পারি তাহলে নিশ্চিত ভাবে বলা যায় B প্রবলেমটাও A প্রবলেমের মতোই কঠিন। NP hard প্রবলেমকে অনেক সময় NP ক্যাটাগরিতে ফেলা যায়না কারণ সেটা পলিনমিয়াল টাইমে ভেরিফাই করা যায় না।
NP কে পলিনমিয়াল টাইমে সলভ করা যায়না, ভেরিফাই করা যায়। NP hard কে পলিনমিয়াল টাইমে সলভ করা যায়না, ভেরিফাই করা যেতেও পারে, নাও যেতে পারে।
তাহলে আমরা এখন পর্যন্ত যতটুক জেনেছি:
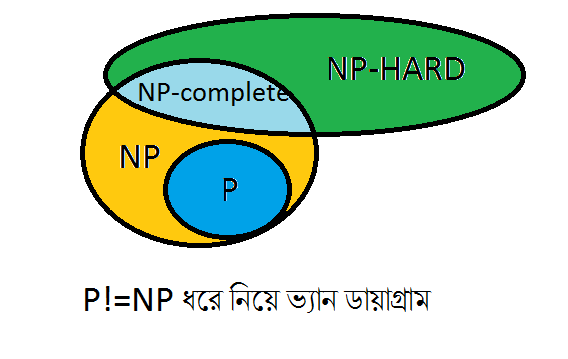
যদি কখনো প্রমাণ হয় যে P=NP তাহলে ছোট নীল সার্কেলটা আর দরকার হবে, হলুদ সার্কেলে P=NP লিখে দেয়া যাবে। NP-hard ক্যাটাগরির যেসব প্রবলেম পলিনমিয়াল টাইমে ভেরিফাই করা যায় সেগুলো NP ক্যাটাগরিতে, বাকিগুলো বাইরে। নীল অংশের প্রবলেমগুলো দুটো ক্যাটাগরিতে কমন, সেগুলোর নাম কি?
NP complete: একটা প্রবলেম NP-complete হবে কেবল যদি প্রবলেমটা NP-hard হয় এবং সেটা NP ক্যাটাগরীতেও পড়ে। NP complete প্রবলেমকে পলিনমিয়াল টাইমে অন্য যেকোনো NP প্রবলেমে কনভার্ট করা যায় এবং এই প্রবলেমের সার্টিফিকেটকে পলিনমিয়াল টাইমে ভেরিফাইও করা যায়।
একটা প্রবলেম NP-hard প্রমাণ করতে হলে আমাদের সেটাকে পরিচিত কোনো NP-complete প্রবলেমকে সেই প্রবলেমে কনভার্ট করতে হবে। যেমন লংগেস্ট পাথ প্রবলেমে বলা হয়েছে গ্রাফে সবথেকে লম্বা পাথ বের করতে হবে যেন কোনো নোড সেই পাথে দুইবার না থাকে। হ্যামিল্টনিয়ান পাথ একটা পরিচিত NP-complete প্রবলেম, গ্রাফে যদি হ্যামিল্টনিয়ান পাথ থাকে তাহলে সবথেকে লম্বা পাথে n – 1 টা এজ থাকবে কারণ n টা নোড একবার করে ভিজিট করতে হবে। হ্যামিল্টন প্রবলেমকে আমরা একটু ভিন্ন ভাবে বলতে পারি “একটা গ্রাফে কি এমন কোনো পাথ থাকা সম্ভব যেটায় k টা এজ আছে?”, k=n-1 এর জন্য প্রবলেমটা সলভ করতে পারলে হ্যামিল্টন পাথের প্রবলেম সলভ হয়ে যাবে। এবং এই প্রবলেমটা সলভ করতে পারলে k এর বিভিন্ন মানের জন্য সলভ করে সবথেকে লম্বা পাথও বের করতে পারবো! তাহলে দেখা যাচ্ছে হ্যামিল্টন পাথ প্রবলেমকে একটু ভিন্ন ভাবে বর্ণনা করে আমরা লংগেস্ট পাথ প্রবলেমে কনভার্ট করলাম। যেহেতু হ্যামিল্টন পাথের পলিনমিয়াল সলিউশন আমরা জানিনা, লংগেস্ট পাথেরও জানিনা।
এবার হয়তো তুমি বুঝতে পারছো একটা মাত্র প্রবলেম পলিনমিয়াল টাইমে সলভ করতে পারলে কেন সবগুলো করা যাবে।
ডিসিশান প্রবলেম হলো সেগুলো যেগুলোকে yes/no দিয়ে উত্তর দেয়া যায়। যেমন A থেকে B তে কি 10 সেকেন্ডে পৌছানো সম্ভব? অপটিমাইজেশন প্রবলেম অ্যান্সারকে মিনিমাইজ বা ম্যাক্সিমাইজ করে। যেমন A থেকে B তে সব থেকে কম কত সেকেন্ডে পৌছানো সম্ভব। উপরের ক্যাটাগরিগুলো প্রবলেমের ডিসিশান ভার্সন নিয়ে কাজ করে। যেকোনো অপটিমাইজেশন প্রবলেমকেই একটু ভিন্নভাবে বর্ণনা করে ডিসিশান প্রবলেম বানিয়ে ফেলা যায় যেটা আমরা উপরে হ্যামিল্টন পাথের ক্ষেত্রে করেছি।
এখন প্রশ্ন হলো প্রথম np-complete প্রবলেমটা কি? প্রথম একটা np-complete প্রবলেম না থাকলে আমরা অন্য প্রবলেমকে np-complete বা hard ক্যাটাগরিতে ফেলতে পারছিনা যেহেতু আমরা এটা করছি প্রবলেমকে কনভার্ট করে। ধরা যাক তোমার কাছে কিছু বুলিয়ান ভ্যারিয়েবল আছে x,y,z ইত্যাদি। তুমি কিছু শর্ত দিলে এরকম: “X সত্যি হলে Y মিথ্যা”, “Z এবং X দুইটাই মিথ্যা” ইত্যাদি। এখন তোমাকে x,y,z এ true/false ভ্যালু অ্যাসাইন করতে হবে যেন সব রিলেশন সত্যি হয়। এটাকে বলা হয় বুলিয়ান স্যাটিসফাইবিলিটি প্রবলেম বা সংক্ষেপে স্যাট প্রবলেম। রিলেশনে ২টি ভ্যারিয়েবল থাকলে ২-স্যাট প্রবলেম, ৩টি থাকলে ৩-স্যাট, যেমন “X এবং Y মিথ্যা হলে Z সত্য” এরকম রিলেশন থাকলে সেটা ৩-স্যাট, জেনারেলাইজ করে বলা হয় k-sat। ২-স্যাটকে পলিনমিয়াল টাইমে সলভ করা যায়, k>2 হলে পলিনমিয়াল সলিউশন পাওয়া যায়না। NP ক্যাটাগরির ফর্মাল ডেফিনেশন ব্যবহার করে Cook–Levin প্রমাণ করে k-sat একটি NP complete প্রবলেম। এটাই ছিল প্রথম প্রমাণ। Cook পরবর্তিতে কম্পিউটার সায়েন্সের সর্বোচ্চ টুরিং পুরস্কার পান তার কাজের জন্য। k-sat প্রবলেম যদি তুমি পলিনমিয়াল টাইমে সলভ করতে পারো চোখের নিমেষে তুমি আইনস্টাইন-নিউটন টাইপের মানুষের সমতুল্য হয়ে যাবে।
টুরিঙ এর একটা বিখ্যাত NP-hard প্রবলেম হলো হাল্টিং প্রবলেম। “একটা কম্পিউটার প্রোগ্রাম দেয়া হলো, বলতে হবে এটা কখনো শেষ হবে নাকি অসীম সময় ধরে চলতে থাকবে”। এটাকে পলিনমিয়াল টাইমে সলভ বা ভেরিফাই কিছুই করা যায় না। বিস্তারিত জানতে আমার এই লেখাটা পড় কিন্তু তার আগে একটা কমিকস পড়ি:
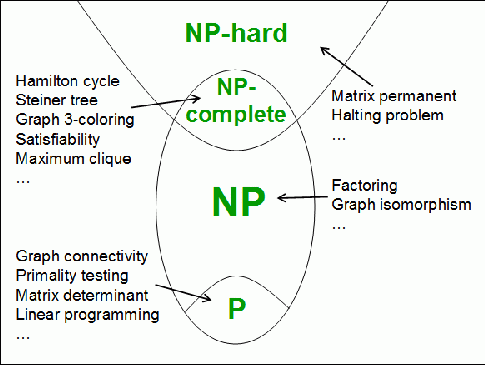
নিচের ছবিতে প্রতিটা ক্যাটগরির কিছু প্রবলেম দেখানো হয়েছে:
প্রোগ্রামিং কনটেস্টে প্রায়ই NP প্রবলেম দেখা যায় তবে সেখানে ইনপুটের সাইজ অনেক কমিয়ে দেয়া হয় বা বিশেষ কোনো কন্ডিশন যোগ করে দেয়া হয় যাতে ব্যাকট্র্যাকিং করে ৩-১০ সেকেন্ডের মাঝে সলভ করা সম্ভব হয়। অনেক রিয়েল লাইফ সমস্যার পলিনমিয়াল সলিউশন না থাকায় বিজ্ঞানীরা চেষ্টা করছেন এক্সপোনেন্টসিয়াল সলিউশনকেই যতটা সম্ভব উন্নত করার। ব্রাঞ্চ এন্ড বাউন্ড টেকনিকের সাহায্যে ব্যাকট্র্র্যাকিঙ এ সার্চ স্পেস কমিয়ে মোটামুটি দ্রুত সলিউশন বের করা যায়। অনেক সময় হিউরিস্টিক এর সাহায্য নেয়া হয়। ট্রাভেলিং সেলসম্যান, গ্রাফ কালারিং ইত্যাদি সলভ করার জন্য অনেক আ্ধুনিক অ্যালগোরিদম আছে, এগুলো নিয়ে এখনো রিসার্চ চলছে, তোমার আগ্রহ থাকলে কিছু রিসার্চ পেপার নামিয়ে নিজেই পড়ালেখা করতে পারো।
রেফারেন্স:
http://www.quora.com/What-are-P-NP-NP-complete-and-NP-hard
http://stackoverflow.com/questions/1857244/np-vs-np-complete-vs-np-hard-what-does-it-all-mean
http://en.wikipedia.org/wiki/P_versus_NP_problem
Introduction to Algorithms by Coreman
http://en.wikipedia.org/wiki/Hamiltonian_path_problem
http://www.princeton.edu/~achaney/tmve/wiki100k/docs/Non-deterministic_Turing_machine.html
http://plato.stanford.edu/entries/turing-machine/#Computability
তানভীরুল ইসলামকে ধন্যবাদ নন-ডিটারমিনিস্টিক এর ব্যাপারটা আমাকে বুঝিয়ে বলার জন্য।
ফেসবুকে মন্তব্য
Powered by Facebook Comments


দারুন। 🙂
একটু টাইপো আছে। প্রথম ভ্যান ডায়াগ্রামের চিত্রটার নীচে প্রথম লাইনে সম্ভবত একটা ‘না’ বাদ গেছে।
আর রেফারেন্সের প্রথম লিংকটা ঠিক নেই, অন্য সাইটে রিডাইরেক্ট করতেছে।