মিট ইন দ্যা মিডল খুবই এলিগেন্ট একটা প্রবলেম সলভিং টেকনিক। এটার কাজ হলো প্রবলেমটাকে ঠিক দুইভাগে ভাগ করে ফেলে তারপর সেই দুইভাগকে কোনোভাবে মার্জ করে প্রবলেমটা সলভ করা। তবে ডিভাইড এন্ড কনকোয়ারের সাথে এটার পার্থক্য হলো ডিভাইড এন্ড কনকোয়ারে দুই ভাগে ভাগ করার পর ছোট ভাগগুলোকে বারবার ভাগ করা হয়, মিট ইন দ্যা মিডলে আমরা শুধু একবার ভাগ করবো।
আমরা কিছু প্রবলেম দেখবো যেগুলোকে মিট ইন দ্যা মিডলের সাহায্যে সলভ করা সম্ভব।
প্রবলেম ১: সাম অফ ফোর
(দরকারি নলেজ: বাইনারি সার্চ)
তোমাকে ৪টা $n$ সাইজের অ্যারে A,B,C,D দেয়া আছে। প্রতিটা অ্যারে থেকে এক্স্যাক্টলি একটা করে ভ্যালু সিলেক্ট করতে হবে যেন তাদের যোগফল ০ হয়।
যেমন $n=3$ এবং A=$\{1,2,3\}$, B=$\{-1,-4,-5\}$, C=$\{1,5,8\}$, D=$\{9,8,5\}$ হলে $1+(-4)+8-5=0$ হতে পারে একটা সলিউশন।
সলিউশন-১
প্রথমেই মাথায় যে সলিউশন আসে সেটা হলো ৪টা নেস্টেড লুপ চালিয়ে সব কম্বিনেশনে সংখ্যাগুলোকে যোগ করে দেখা। এটার কমপ্লেক্সিটি হবে $O(n^4)$। যদি $n=1000$ হয় তাহলে প্রোগ্রামটা শেষ হতে কয়েক ঘন্টা লেগে যাবে।
আমাদের ৪টা মান $a,b,c,d$ দরকার যাতে $a+b+c+d=0$ হয়। এটাকে লেখা যায়, $(a+b)=-(c+d)$। a ভ্যালুটা পাবো A অ্যারে থেকে, b পাবো B অ্যারে, c পাবো C অ্যারে থেকে এবং d পাবো D অ্যারে থেকে।
এখন দুটি নেস্টেড লুপ চালিয়ে A এবং B অ্যারে দিয়ে যতগুলো কম্বিনেশন বানানো যায় সবগুলো বের করে ফেলি। তাহলে আমরা সবগুলো (a+b) পেয়ে গেলাম। সবগুলো ভ্যালুকে সর্ট করে রাখো বা ম্যাপে ইনসার্ট করে রাখো।
আবার দুটি নেস্টেড লুপ চালিয়ে C এবং D অ্যারে দিয়ে যতগুলো কম্বিনেশন বানানো যায় সবগুলো বের করি। এখন পেলাম সবগুলো c+d। প্রতিটা c+d এর জন্য a+b খুজে বের করো আগের সর্টেড ভ্যালুতে বাইনারি সার্চ চালিয়ে বা ম্যাপের মধ্যে খুজে।
এখন আমাদের কমপ্লেক্সিটি হলো $O(n^2*logn^2)$ । যদি ভ্যালুগুলো ছোটো হয় তাহলে ম্যাপের জায়গায় সাধারণ বুলিয়ান ফ্ল্যাগ ব্যবহার করে $O(n^2)$ এ সলভ করা সম্ভব।
প্রবলেম ২: কয়েন চেঞ্জ
(দরকারি নলেজ: বাইনারি সার্চ, ব্যাকট্র্যাকিং অথবা বিটমাস্ক ব্যবহার করে সবগুলো সাবসেট জেনারেশন)
ধরো তোমার কাছে কিছু কয়েন আছে। বলতে হবে এগুলো থেকে কিছু কয়েন ব্যবহার করে নির্দিষ্ট একটা ভ্যালু তৈরি করা যায় নাকি। কোনো কয়েন একবারের বেশি ব্যবহার করা যাবেনা। যেমন কয়েনগুলো যদি হয় ১,৩,৬,১০ তাহলে তুমি ১৩ বা ১১ বানাতে পারবে কিন্তু ৫০ বা ২ কিছুতেই বানাতে পারবেনা। কয়েনের সংখ্যা সর্বোচ্চ ৩০টা।
সলিউশন
মনে করি কয়েনগুলার মান হতে পারে ১ থেকে ১০০ পর্যন্ত। তুমি যদি ডাইনামিক প্রোগ্রামিং জানো তাহলে নিশ্চয়ই ভাবছো এটাতে খুব সহজ প্রবলেম, সবগুলো কয়েনের ভ্যালুর যোগফল সর্বোচ্চ হতে পারে ৩০*১০০, তাহলে ৩০*(৩০*১০০) কমপ্লেক্সিটিতে খুব সহজে প্রবলেমটা সলভ করা যাবে। এবার আমি প্রবলেমটাকে কঠিন করে দেই, ধরি কয়েনগুলোর ভ্যালু হতে পারে ১ থেকে ১০^৯। এখন কমপ্লেক্সিটি হয়ে গেলো ৩০*(৩০*১০^৯)। এটা ডাইনামিক প্রোগ্রামিং দিয়ে সলভ করা সম্ভবনা, মেমরি বা টাইম কোনোটাতেই কুলিয়ে উঠবেনা। এখন কি করা যেতে পারে? এখানে লক্ষ্য করার বিষয় হলো কয়েনের সংখ্যা অনেক কম!
কয়েনের সংখ্যা মাত্র ৩০ হলেও ৩০টা কয়েনের একটা সেটের সাবসেট সংখ্যা ২^৩০। তারমানে সর্বোচ্চ ২^৩০টা ভিন্ন ভ্যালু তৈরি করা যাবে কয়েনগুলো দিয়ে। তাই ব্যাকট্র্যাকিং করে সবগুলো ভ্যালু জেনারেট করা পসিবল না। কিন্তু কয়েন যদি ১৫টা হতো তাহলে ২^১৫=৩২৭৬৮টা সাবসেট থাকতো এবং সবগুলো ভ্যালু আমরা জেনারেট করতে পারতাম ব্যাকট্র্যাক করে! এই পর্যন্ত পড়ার পর একটু থেমে কিছুক্ষণ চিন্তা করো কিভাবে প্রবলেমটা সলভ করা সম্ভব। এরপরে নিচের অংশ পড়ো।
আমরা কয়েনগুলোকে দুই ভাগে ভাগ করে ফেলি। প্রতিটা ভাগে আছে ১৫টা করে কয়েন। এখন প্রথম ভাগের ১৫টা কয়েন নিয়ে সবগুলো ভ্যালু জেনারেট করে একটা অ্যারেতে রেখে দাও, মনে করি অ্যারেটার নাম A। একই ভাবে ২য় ১৫টা কয়েন নিয়ে সবগুলো ভ্যালু জেনারেট করে আরেকটা অ্যারেতে রেখে দাও, মনে করি অ্যারেটার নাম B। B অ্যারেটাকে সর্ট করে ফেলো, A কে সর্ট করার দরকার নেই।
এখন বাকি কাজ সহজ। মনে করো তোমাকে X ভ্যালুটা বানাতে হবে। A অ্যারের উপর লুপ চালিয়ে সবগুলো ভ্যালু চেক করো। i তম ভ্যালু যদি হয় A[i] তাহলে তুমি চেক করো B অ্যারেতে X-A[i] ভ্যালুটা আছে নাকি। যদি থাকে তাহলে তুমি X বানাতে পারবে!! B তুমি সর্ট করে রেখেছো, তাহলে বাইনারি সার্চ করেই X-A[i] আছে নাকি চেক করতে পারবে। একটু ভাবলেই বুঝতে পারবে A অ্যারেতে প্রথম ১৫টার সবরকম কম্বিনেশন আছে, তাই X-A[i] কে A তে খোজার কোনো দরকার নাই।
n টা কয়েনের জন্য তাহলে কমপ্লেক্সিটি হবে O(2(n/2)*log2(n/2)), কারণ আমরা 2(n/2) টা ভ্যালুর জন্য বাকি অর্ধেকের উপর বাইনারি সার্চ করছি।
প্রবলেম ৩: বাইডিরেকশনাল সার্চ
(দরকারি নলেজ: গ্রাফ থিওরি)
একটা গ্রাফে দুটি নোড দেয়া আছে, নোড দুটির মধ্যে শর্টেস্ট পাথ বের করতে হবে।
সলিউশন:
মোটামুটি নিশ্চিত গ্রাফ থিওরি যারা পারো তারা মাথা চুলকিয়ে ভাবছো, এটা কোনো প্রবলেম হলো? বিএফএস দিয়েইতো সলভ করা যায়। কিন্তু এখানে আমরা চিন্তা করছি বিশাল গ্রাফের কথা যেখানে বিলিয়ন বিলিয়ন নোড আর এজ থাকতে পারে।
বিএফএস এ প্রতিটা নোড থেকে তার অ্যাডজেসেন্ট নোডগুলোতে যেতে হয়, সেগুলো থেকে আবার তার অ্যাডজেসেন্ট নোডগুলোতে যেতে হয়। প্রতিটা নোডের অ্যাডজেসেন্ট নোড সংখ্যাকে বলা হয় নোডটা ডিগ্রী। এখন যদি প্রতিটা নোডের এভারেজ ডিগ্রী হয় p আর শর্টেস্ট পাথ যদি হয় k তাহলে তোমাকে মোটামুটি O(pk) টা নোড এক্সপ্লোর করতে হবে।
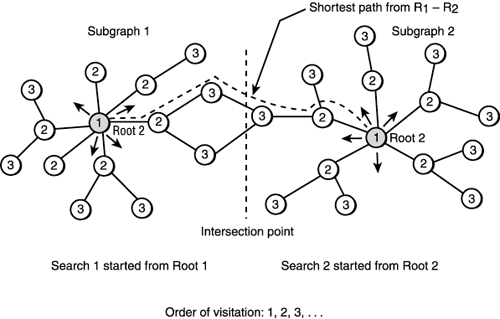
যদি তুমি সোর্স আর ডেস্টিনেশন দুই পাশ থেকে সার্চ শুরু করো যতক্ষণনা তারা একসাথে মিলছে তাহলে কমপ্লিক্সিটি হয়ে যাবে O(pk/2)। আগের কয়েন চেঞ্জ প্রবলেম সলভ করেই বুঝতে পারছো এই অর্ধেক হওয়াটা এক্সপোনেনশিয়াল কমপ্লেক্সিটির ক্ষেত্রে এটা খুবই সিগনিফিকেন্ট উন্নতি।
গ্রাফ রিলেটেড আরো দুটি ইন্টারেস্টিং প্রবলেম হলো:
১. ফেসবুকের গ্রাফে দুজন ইউজারের মধ্যে মিউচুয়াল ফ্রেন্ড আছে নাকি বের করতে হবে
২. ধারণা করা হয় সোস্যাল নেটওয়ার্কে যেকোনো দুজন মানুষের দূরত্ব সর্বোচ্চ ৬টি নোড। দুটি ইউজারনেম ইনপুট দিলে কিভাবে এটা ভেরিফাই করবে?
রেফারেন্স: ইনফো এরিনা
কৃতজ্ঞতা: মাহবুবুল হাসান শান্ত ভাইকে ধন্যবাদ সাম অফ ফোর প্রবলেমের সলিউশনে ভুল ধরিয়ে দেয়ার জন্য।
সলভ করার জন্য প্রবলেম:
Coin Change(IV)
Sum of Four
Funny Knapsack
হ্যাপি কোডিং!
ফেসবুকে মন্তব্য
Powered by Facebook Comments

ভাই ডিভাইড এন্ড কনকোয়া্র সম্পরকে কিছু বলেন
ভাই খালি TLE খাই MAP use করছি কিনতু লাভ হোয় না
sum of four