বাইনারি ইনডেক্স ট্রি খুবই চমৎকার একটা ডাটা স্ট্রাকচার যার সবথেকে ভালো দিক হলো কয়েক মিনিটেই কোড লিখে ফেলা যায়। আর খারাপ দিক হলো ভিতরে কি হচ্ছে বুঝতে একটু কষ্ট হয়, তবে তুমি লেখাটা মনযোগ দিয়ে পড়লে আমি নিশ্চিত কোন সমস্যা হবে না। বাইনারি ইনডেক্সড ট্রি বা BIT এর আরেক নাম হলো ফেনউইক(fenwick) ট্রি। এই লেখাটা পড়ার আগে তোমাকে বিটওয়াইজ অপারেশনগুলো(AND,OR ইত্যাদি) সম্পর্কে ভালো জানতে হবে।
আমরা একটা সহজ সমস্যা সমাধান করতে করতে বাইনারি ইনডেক্স ট্রি সম্পর্কে জানব। এই লেখায় আমরা ধরে নিব অ্যারের ইনডেক্স ১ থেকে শুরু, BIT কিভাবে কাজ করে জানার পরে বুঝতে পারবে এটা কেন গুরুত্বপূর্ণ। তোমাকে একটা অ্যারে দেয়া হলো যার প্রতিটি পজিশনে ০ আছে। এখন তোমাকে অনেকগুলো অপারেশন দেয়া হবে। প্রতিটা অপারেশন হতে পারে নিচের যেকোন একটা:
* $i$ তম ইনডেক্সে $x$ সংখ্যাটা যোগ কর।
* $1$ থেকে $i$ তম ইনডেক্সের সাবঅ্যারের মোট যোগফল বল।
একদম ‘নেইভ(Naive)’ উপায়ে করলে আমরা $O(1)$ এ প্রতি পজিশনে $x$ যোগ করব আর লুপ চালিয়ে $O(n)$ এ যোগফল বের করব। BIT দিয়ে যোগফল O(logn) এ বের করা সম্ভব, তবে সেক্ষেত্রে আপডেট অপারেশনও $O(log \times n)$ এ করতে হবে।
আমরা জানি প্রতিটা সংখ্যাকেই কিছু ২ এর পাওয়ারের যোগফল হিসাবে লেখা যায়। যেমন ১৩ এর বাইনারি হলো “১১০১”, বাইনারিতে ১ আছে ০তম, ২য় এবং ৩য় অবস্থানে। তাহলে ১৩ কে লেখা যায় ২^০+২^২+২^৩ বা ১+৪+৮। বাইনারি ইনডেক্স ট্রি তে আমরা এই প্রোপার্টিটা ব্যবহার করে কিছু কাজ করব। যে সংখ্যাটা অ্যারেতে যোগ করছি সেটাকে নয় বরং আমরা অ্যারের ইনডেক্সগুলোকে ২ এর পাওয়ারে যোগফল হিসাবে লিখে কিছু কাজ করব।
$1$ থেকে $i$ পর্যন্ত অ্যারের সামকে আমরা অ্যারের কিছু সেগমেন্টের যোগফল হিসাবে লিখতে পারি। মনে কর আমাদের একটা $sum(i, j)$ ফাংশন আছে যার কাজ হলো $i$ থেকে $j$ ইনডেক্সের মধ্যে অ্যারের সবগুলো এলিমেন্টের যোগফল বের করা। তাহলে ১৩ তম ইনডেক্সের এর জন্য যোগফল হতে পারে $sum(1, 5)+sum(6, 10)+sum(11, 12)$। এখানে ১৩কে আমরা ৩টি সেগমেন্টে ভাগ করেছি। বাইনারি ইনডেক্স ট্রি তে আমরা প্রতিটি সংখ্যাকে কিছু সেগমেন্টে ভাগ করব। তবে উপরে যেভাবে করেছি সেভাবে ইচ্ছামত করলে হবে না, এটা আমরা একটু বুদ্ধিমানের মত করব। যেহেতু “বাইনারি ইনডেক্সড ট্রি” ব্যবহার করব, তাই বুঝতে পারছ হয়ত যে অ্যারের ইনডেক্সগুলোর বাইনারি রিপ্রেজেন্টশনকে ব্যবহার করে কোন কাজ করতে হবে।
কোন সংখ্যাকে যেহেতু ২এর পাওয়ারের যোগফল হিসাবে লেখা যায়, তারমানে সংখ্যাটা থেকে ২এর পাওয়ার বিয়োগ দিতে দিতে আমরা ০ বানিয়ে ফেলতে পারি। ১৩ থেকে একে একে ১, ৪ এবং ৮ বাদ দিলে আমরা পাবো:
১৩-১=১২
১২-৪=৮
৮-৮=০
তাহলে ১৩ এর জন্য সেগমেন্ট হবে $sum(1, 8) + sum(9, 12) + sum(13, 13)$। আরেকটা উদাহরণ দেখলে পরিস্কার হবে, ৬(বাইনারিতে ১১০)=২^১+২^২ এর জন্য একই ভাবে লিখতে পারি:
৬-২=৪
৪-৪=০
এবার তাহলে ৬ এর জন্য সেগমেন্ট হবে $sum(1,4) + sum(5,6)$।
কোড কিভাবে করব সেটা এখন চিন্তা করা দরকার নেই, তুমি শুধু চিন্তা কর গাণিতিকভাবে ভাগটা কিভাবে করা হচ্ছে সেটা তুমি বুঝতে পারছ নাকি। এখন আমরা সেগমেন্টগুলো ছবিতে দেখব:
ছবিতে ১ এর জন্য সেগমেন্টটা চিহ্নিত করা হয়েছে। এরপরে আমরা ২এর জন্য করব। ২ এর জন্য উপরের মত করে লিখতে পারি:
২-২=০
তাই সেগমেন্টটা হবে ১থেকে ২পর্যন্ত।
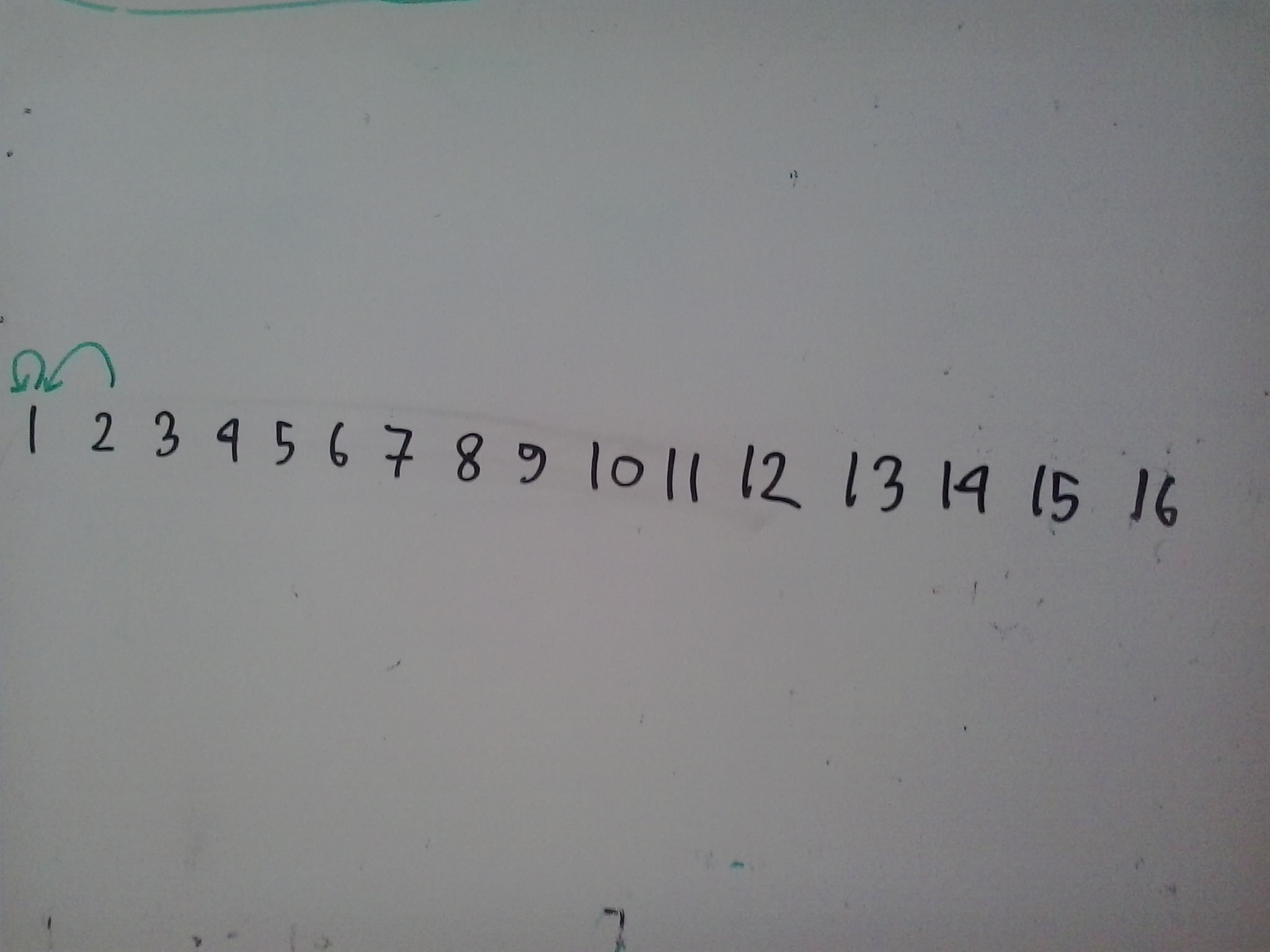 এখন তোমার কাজ ১৬ পর্যন্ত সবগুলো সংখ্যার জন্য এভাবে সেগমেন্ট একে ফেলা। কিভাবে সেগমেন্ট তৈরি হচ্ছে বোঝাটা বাইনারি ইনডেক্সড ট্রি এর সবথেকে দরকারি অংশ, তাই না বুঝলে আবার ভাল করে পড়। তোমার আকার সাথে নিচের ছবিটি মিলিয়ে দেখ:
এখন তোমার কাজ ১৬ পর্যন্ত সবগুলো সংখ্যার জন্য এভাবে সেগমেন্ট একে ফেলা। কিভাবে সেগমেন্ট তৈরি হচ্ছে বোঝাটা বাইনারি ইনডেক্সড ট্রি এর সবথেকে দরকারি অংশ, তাই না বুঝলে আবার ভাল করে পড়। তোমার আকার সাথে নিচের ছবিটি মিলিয়ে দেখ:
এই ছবি দেখেই আমরা প্রতিটা সংখ্যার জন্য সেগমেন্টগুলো বলে দিতে পারি। যেমন ১১ এর জন্য সেগমেন্টগুলো হবে $(11, 11), (10, 9), (8, 1)$। তুমি যদি নিজে বুঝে উপরের ছবিটা একে থাকো তাহলে তুমি বুঝে গেছ কিভাবে ছবি দেখে সেগমেন্ট বের করে ফেললাম।
আমরা আগেই $sum(i,j)$ ফাংশন ডিফাইন করেছি। কিন্তু সেই ফাংশনটা ব্যবহার করলে আমাদেরকে $i$ থেকে $j$ তে লুপ চালিয়ে যোগফল বের করতে হবে যেটা আমরা চাইনা। আমরা আরেকটা অ্যারে ডিফাইন করব $Tree[]$। তুমি ছবিতে দেখতে পাচ্ছ অ্যারের প্রতিটি ইনডেক্স একটা সাবঅ্যারেকে কভার করে। যেমন ১২ নম্বর ইনডেক্স (৮,১২) সাবঅ্যারেকে কভার করে। আমরা এমন কিছু করার চেষ্টা করব যেন $Tree[i]$ তে $i$ তম ইনডেক্স যতটুকু সাবঅ্যারে কভার করে সেটার যোগফল থাকে। তাহলে $Tree[12]$ তে সেভ করা থাকবে $sum(8,12)$, আবার $Tree[14]$ তে সেভ করা থাকবে $sum(13, 14)$।
এই কাজটা যদি করতে পারি তাহলে ১১ নম্বর ইনডেক্সের জন্য $sum(11, 11) + sum(10, 9) + sum(8,1)$ বের না করে আমরা $tree[11]+tree[10]+tree[8]$ বের করলেই যোগফল পেয়ে যাবো।
এখন ধরি আমাকে বলা হল ৫ নম্বর ইনডেক্সে $x$ যোগ করতে চাই। আমাকে এখন বুদ্ধিমানের মত Tree অ্যারেতে কিছু ইনডেক্সে x সংখ্যাটা যোগ করে দিতে হবে। আমরা প্রথমে $Tree[5]$ এ $x$ যোগ করব, এরপরে সবথেকে ছোট সেই ইনডেক্সে করব যেটা উপরের ছবিতে ৫কে কভার করে। সেই ইনডেক্সটা হলো ৬, তাহলে tree[৬] এ $x$ যোগ করব। এরপরে ৬কে কভার করে ৮, তাই tree[৮] এ x যোগ করব। এরপরে একই ভাবে tree[১৬] তে $x$ যোগ করব।
আমরা tree অ্যারেতে ছবিতে তীর চিহ্ন দেয়া ইনডেক্সগুলোতে $x$ যোগ করব। এখানে লক্ষ্য করার বিষয় হলো উপরে লেখা পদ্ধতিতে যোগফল বের করার সময় তুমি এই ৩টা ইনডেক্সের সর্বোচ্চ যেকোন এক্সেস করতে পারবে। যেমন ১৬ তে এক্সেস করলে সরাসরি ৫,৮ ইত্যাদিকে স্কিপ করে সরাসরি ১ এ চলে যেতে হবে। এই প্রোপার্টিটা থাকার কারণে একই আপডেট দুইবার গুণে ফেলার সম্ভাবনা নেই। আপডেট অপারেশন ঠিকমত বুঝেছো নাকি পরীক্ষা করতে ৯ এর জন্য উপরের মত করে তীরচিহ্ন বসায় এবং তারপর নিচের সমাধানের সাথে মিলিয়ে দেখ:
ছবিতে ৯থেকে শুরু করে প্রতিবার এমন ইনডেক্সে গিয়েছি যেটা আগের ইনডেক্সটাকে পুরোটা কভার করে। যোগফল বের করার সময় কোনভাবেই এই ৪টা ইনডেক্সের একটার বেশি এক্সেস করা সম্ভব না!
এবার আমরা কোডের দিকে যাবো। প্রথমেই কুয়েরি অপারেশনটা ইমপ্লিমেন্ট করব। কোন সংখ্যা ২ এর পাওয়ার হলে তার বাইনারি রিপ্রেজেন্টশন হয় ১, ১০,১০০,১০০০,১০০..০০ এরকম, অর্থাৎ ১ এর পর কিছু শূন্য। এখন ১১ নাম্বার ইনডেক্সের জন্য কুয়েরি করতে চাই। ১১ কে বাইনারিতে লিখতে পারি ১০১১। আমরা প্রথমেই সবথেকে ডানের ১ খুজে বের করব এবং সেই পজিশন থেকে বাকি অংশটা মূল সংখ্যা থেকে বিয়োগ দিব। তাহলে শুরুতেই বিয়োগ হবে ১।
১০১১-১=১০১০ (অথবা দশমিক পদ্ধতিতে ১১-১=১০)
আবারো সব থেকে ডানের ১ থেকে শুরু করে বাকিটা বিয়োগ দিলে পাব:
১০১০-১০=১০০০ (অথবা দশমিক পদ্ধতিতে ১০-২=৮)
এভাবে বিয়োগ করতে থাকবো যতক্ষণ শূন্য না পাই।
১০০০-১০০০=০ (অথবা দশমিক পদ্ধতিতে ৮-৮=০)
লক্ষ্য কর ১১ এর জন্য দরকারি ৩টা ইনডেক্স ১১,১০,৮ আমরা পেয়ে গিয়েছি ২এর পাওয়ার বিয়োগ করে করে! ১৩ বা বাইনারিতে ১১০১ এর জন্য নিজে কর এবং তারপর নিচের সমাধান দেখ:
১১০১-১=১১০০ (অথবা দশমিক পদ্ধতিতে ১৩-১=১২)
১১০০-১০০=১০০০ (অথবা দশমিক পদ্ধতিতে ১২-৪=৮)
১০০০-১০০০=০ (অথবা দশমিক পদ্ধতিতে ৮-৮=০)
১৩ এর জন্য দরকারি ইনডেক্স ১৩,১২,৮ পেয়ে গিয়েছি!
এখন প্রশ্ন হল এই কাজটা কোডে করব কিভাবে? লুপ চালিয়ে একটা একটা বিট পরীক্ষা করে করা যেতে পারে কিন্তু কাজ O(1) এই করা যায়। idx নম্বর ইনডেক্সের পরের ইনডেক্সটা হবে:
idx=idx – (idx & -idx)
এটা কিভাবে কাজ করে বোঝার জন্য খাতাকলমে বিয়োগটা করে দেখ আমার ব্যাখ্যা পড়ার আগেই! আমি একটা উদাহরণ দিচ্ছি, ধরি idx=১০ বা বাইনারিতে ১০১০। তাহলে 2’s complement পদ্ধতিতে -idx বা -১০ হবে ০১০১+১=০১১০। (যারা ভুলে গেছ তাদের জন্য, 2’s কমপ্লিমেন্ট বের করতে বিটগুলোকে উল্টে দিয়ে ১ যোগ করতে হয়।) এবার যদি বিটওয়াইজ AND করি তাহলে পাবো:
1010
0110
——-
0010
সবথেকে ডানের ১ থেকে বাকি অংশ পেয়ে গেলাম! এবার বিয়োগ করে দিলেই কাজ শেষ। এটা কেন কাজ করছে? আমরা বাইনারি সংখ্যাটাকে ৩টা অংশে ভাগ করতে পারি x1z। 1 হলো সবথেকে ডানের ১, x হলো তার আগের যেকোন বিট, z হলো ১ এর পরের থাকা o বিট(x বা z এ শূণ্যটা, একটা বা একাধিক বিট থাকতে পারে। এখন বিটগুলো উল্টেদিলে পাবো: x’0z’। x বা z অংশের বিটগুলোকে উল্টে দিয়ে পেয়েছি x’ আর z’, তারমানে z’ হলো কিছু ১ বিট। 2’s কমপ্লিমেন্ট বের করতে ১ যোগ করলে পাবো: x’1z। এখন আগের সংখ্যা x1z আর x’1z কে AND করলে থাকে 1z। x এর ভাগটা পুরোটা শূণ্য হয়ে যাবে তাই সেটা বাদ। তাহলে আমরা ডানের ১থেকে বাকি অংশ পেয়ে যাবো!
কোডটা তাহলে খুব সহজ:
|
1 2 3 4 5 6 7 8 |
int query(int idx){ int sum=0; while(idx>0){ sum+=tree[idx]; idx -= idx & (-idx); } return sum; } |
আপডেট অপারেশন কিভাবে করব? ১০১০ বা ১০ এর পরের কোন ইনডেক্সটা ১০ কে কভার করবে? এবার আমরা সবথেকে ডানের ১ কে বামপাশে শিফট করে দিব। ১০১০ এর সাথে ১০ যোগ করলে পাই ১১০০ বা ১২ যেটা ১০কে পুরোটা কভার করে। ঠিক সেরকম ১২ বা ১১০০ এর সাথে ১০০ যোগ করলে পাই ১০০০০ যেটা ১২কে পুরোটা কভার করে। এটা কিভাবে কাজ করছে সেটা চিন্তা করে বের করে ফেল!
আগের মত করেই শুধু বিয়োগের জায়গায় যোগ করলেই সবথেকে ডানের ১টা বামে সরে যাবে। তারমানে যে সংখ্যাটা যোগ করছি, নতুন ইনডেক্স থেকে কুয়েরির সময় তারথেকেও বড় একটা সংখ্যা বিয়োগ করা হবে তাই নতুন ইনডেক্সটা আগেরটাকে কভার করতে বাধ্য! কোডটা হবে এরকম:
|
1 2 3 4 5 6 7 8 |
void update(int idx, int x, int n) //n is the size of the array, x is the number to add { while(idx<=n) { tree[idx]+=x; idx += idx & (-idx); } } |
এটাই হলো বাইনারি ইনডেক্সড ট্রি। এখন আমরা সহজেই কোন একটা ইনডেক্স আপডেট করতে পারব এবং 1 থেকে কোন ইনডেক্স পর্যন্ত যোগফল বের করতে পারব।
কমপ্লেক্সিটি:
আপডেট এবং কুয়েরি সব ক্ষেত্রেই ২ এর পাওয়ার যোগ বা বিয়োগ করছি, প্রথমে ছোট পাওয়ার থেকে শুরু করে বড় পাওয়ার বিয়োগ করছি। তাই টাইম কমপ্লেক্সিটি হবে $O(log \times n)$। শুধুমাত্র Tree অ্যারেটাতেই সব অপারেশন হচ্ছে, স্পেস কমপ্লেক্সিটি $O(n)$।
লক্ষ কর যে এই প্রবলেমটা সেগমেন্ট ট্রি দিয়ে করা গেলেও এখানে মেমরি লাগছে অনেক কম, কোডও খুব ছোট। তবে সেগমেন্ট ট্রিতে বিভিন্ন সব রেঞ্জের ভিতর আপডেট করা যায়, এখানে করা যায় ১ নম্বর ইনডেক্স সহ রেঞ্জে।
প্রবলেম ১: কুয়েরি করার সময় $i$ থেকে $j$ ইনডেক্সের মধ্যের সাবঅ্যারের যোগফল বের করতে বললে কি করবে?
প্রবলেম ২: কুয়েরিতে যদি বলা হয় অ্যারের সর্বনিম্ন কোন ইনডেক্সে গেলে যোগফল X এর বেশি পাবো তাহলে ইনডেক্সটা কিভাবে বের করবে? হিন্টস: O(logn*logn)।
অনলাইন জাজ থেকে কিছু প্রবলেম:
Curious Robin Hood
Inversion Count
Nice Day
২ডি বাইনারি ইনডেক্সড ট্রি এবং আরো কিছু প্রবলেম নিয়ে ভবিষ্যতে লেখার ইচ্ছা আছে। আজকে এই পর্যন্তই। হ্যাপি কোডিং!
ফেসবুকে মন্তব্য
Powered by Facebook Comments
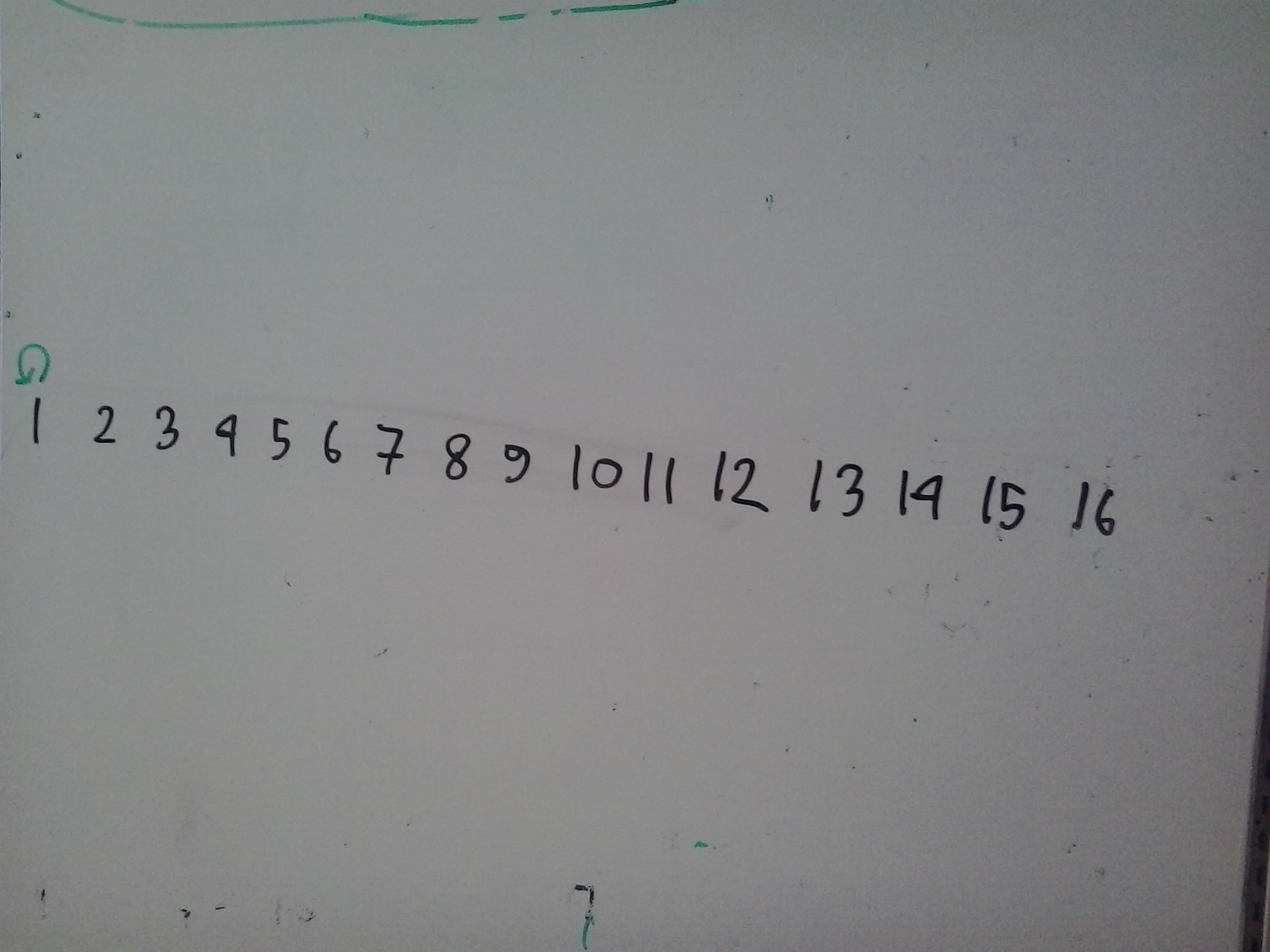
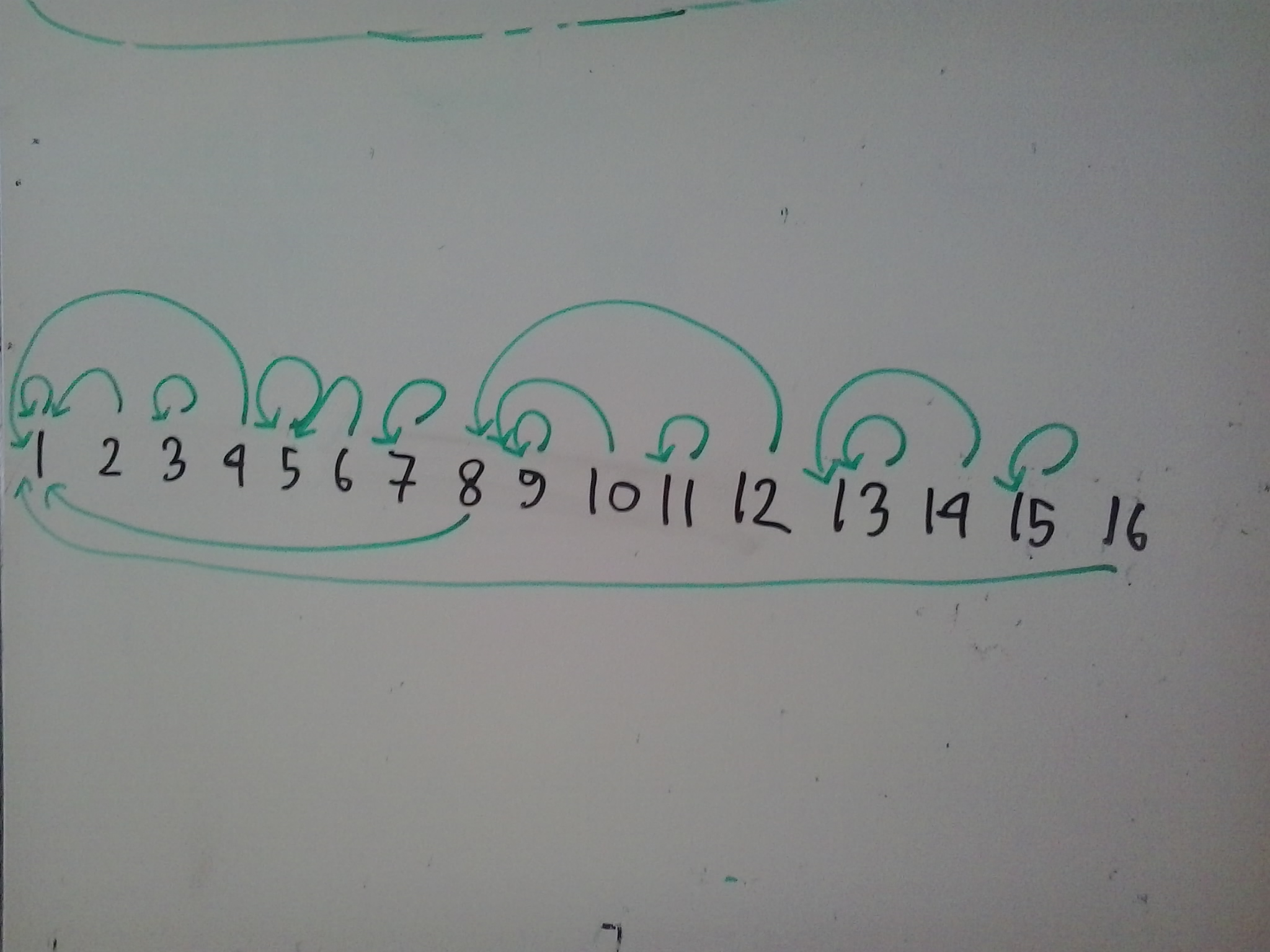
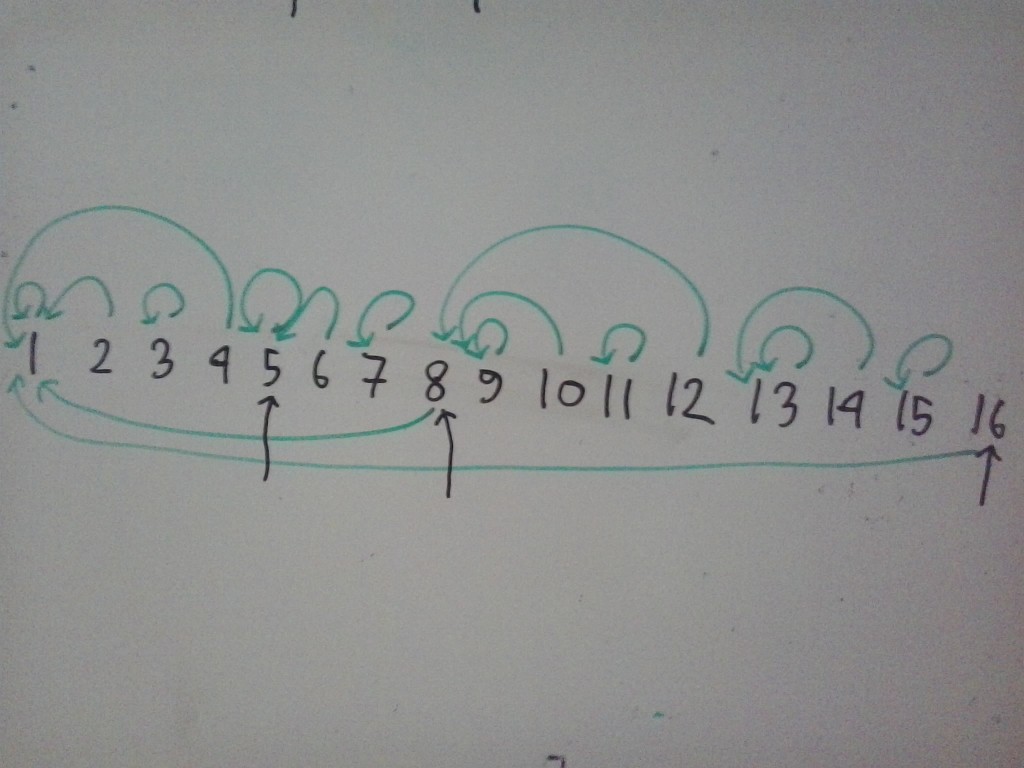


ভাইয়া, ১২ নম্বর ইনডেক্স কি (৯,১২) সাবঅ্যারেকে কভার করে না??
হ্যা। ছবিতে মনে হয় দেখে (৮,১২) মনে হচ্ছে, (৯,১২) হবে।
Update and Query এর while condition টা উল্টো হয়ে গেছে মনে হয়।
🙂
ঠিক করে দিলাম। অনেক ধন্যবাদ।
Is index 5 not covered by index 6?
It is covered.
ভাইয়া, আপনার পোস্টটা আনেক সুন্দর হয়েছে।
picture এর সাইজ আনেক বেশি হওয়াই পেজ লোড হতে আনেক টাইম নিচ্ছে। picture গুলো একটু ছোট করে দিলে আনেক ভাল হত।
এরপর থেকে ছবির ব্যাপারটা মাথায় রাখব। এই পোস্টেতো এখন ছোট করা সম্ভব না, সবগুলো ছবি আবার এডিট করতে হবে। html ট্যাগ দিয়ে ছোট করলে লাভ নাই, একই টাইম লাগবে।
ভাইয়া উপর থেকে চার নম্বর ছবির নিচে লিখা এই অংশটুকু আরেকবার বুঝিয়ে বললে সুবিধা হত 🙂
“এখানে লক্ষ্য করার বিষয় হলো উপরে লেখা পদ্ধতিতে যোগফল বের করার সময় তুমি এই ৩টা ইনডেক্সের সর্বোচ্চ যেকোন এক্সেস করতে পারবে। যেমন ১৬ তে এক্সেস করলে সরাসরি ৫,৮ ইত্যাদিকে স্কিপ করে সরাসরি ১ এ চলে যেতে হবে। এই প্রোপার্টিটা থাকার কারণে একই আপডেট দুইবার গুণে ফেলার সম্ভাবনা নেই।”
ভাইয়া, আগের করা প্রশ্নটির উত্তর দিতে হবেনা, বুঝতে পেরেছি 🙂
চার নাম্বার ছবির উপরে, “এখন ধরি আমাকে বলা হল ৫ নম্বর ইনডেক্সে x যোগ করতে চাই। আমাকে এখন বুদ্ধিমানের মত Tree অ্যারেতে কিছু ইনডেক্সে x সংখ্যাটা যোগ করে দিতে হবে। আমরা প্রথমে Tree[5] এ x যোগ করব, এরপরে সবথেকে ছোট সেই ইনডেক্সে করব যেটা উপরের ছবিতে ৫কে কভার করে। সেই ইনডেক্সটা হলো ৮, তাহলে tree[8] এ x যোগ করব।” এখানে আট এর আগে ৬ আসবে না ? ইনডেক্স ৬ ও তো ৫ কে কভার করে।
হ্যা ৬ হবে, ঠিক করে দিচ্ছি, অনেক ধন্যবাদ।
ভাইয়া……
আপনার পোস্টটা আনেক ভালো হয়েছে ।
অনেক ধন্যবাদ আপনাকে । এত সহজ করে বুঝিয়ে দেওয়ার জন্য ।
৮ কে তো ১২ ও কভার করে কিন্তু ১২ নং ইনডেক্সে x প্লাস হলো না কেন?
Tree[12] তো শুধু ৯-১২ কে কভার করে ।
আপনি লিখলেন “১২ নম্বর ইনডেক্স (৮,১২) সাবঅ্যারেকে কভার করে” ।
নাকি আমি ভুল বুঝলাম ।
একটু ক্লিয়ার করলে ভালো হয় ……
কুয়েরি i থেকে j পর্যন্ত sum বের করতে চাইলে কি (query[j]-query[i] ) এভাবে বের করব?
নাকি আরও ইফিসিয়েন্ট ভাবে করা যাবে???
Here is a technique that can be used to construct Fenwick tree in linear time.
https://youtu.be/BHPez138yX8