আমরা এখন নিম-গেম কিভাবে সমাধান করতে হয় জানি, এখন আমরা গ্রান্ডি সংখ্যা দিয়ে কিছু কম্পোজিট গেম এর সমাধান করবো।

একটা গেম এর কথা চিন্তা করি যেখানে $s$ টা পাথরের একটা স্তুপ(pile) আছে, প্রতিবার কোনো খেলোয়াড় ১টা বা ২টা পাথর তুলে নিতে পারে, শেষ পাথরটা যে তুলে নিবে সে জিতবে। পাথরের সংখ্যা দেখে তোমাকে বলতে হবে অপটিমাল পদ্ধতিতে খেললে প্রথম খেলোয়াড় জিততে পারবে কিনা। প্রথম পর্ব পড়ে থাকলে এটা সমাধান করা তোমার জন্য খুবই সহজ। আমাদের সুডোকোডটা হবে এরকম:

এখন ধরো পাথরের স্তুপের সংখ্যা একটার বদলে যদি $n$ টা এবং প্রতিটা স্তুপে $s_1,s_2……s_n$ টা পাথর আছে। কোনো খেলোয়াড় যেকোনো একটা স্তুপ থেকে ১ বা ২টা পাথর তুলে নিতে পারে, শেষ পাথরটা যে তুলবে সে জিতবে। এবার কিভাবে সমাধান করবে? এধরণের গেমকে কম্পোজিট গেম বলা হয়।

আমরা প্রতিটা স্তুপের জন্য একটা গ্রান্ডি সংখ্যা নির্ধারণ করবো। একটা স্তুপের গ্রান্ডি সংখ্যা g হলে আমরা ধরে নিতে পারি সেই স্তুপটা নিমগেম এ $g$ টা পাথরের একটা স্তুপের সমতুল্য। $n$ টা স্তুপের জন্য আমরা $n$ টা গ্রান্ডি সংখ্যা $g[s_1],g[s_2]….g[s_n]$ পাবো, এবং এরপর নিমগেমের মতো $g[s_1] \oplus g[s_2] \oplus …….. g_n$ বের করলেই আমরা বুঝে যাবো গেমটায় কে জিতবে।

প্রতিটা স্টেট এর জন্য গ্রান্ডি সংখ্যা বের করার নিয়ম হলো, ওই স্টেপ থেকে অন্য যেসব স্টেট এ যাওয়া যায় সেগুলার গ্রান্ডি সংখ্যা প্রথম বের করতে হবে। মনে করো তাদের সেট হলো $X=\{x_1,x_2,…\}$। এখন সর্বনিম্ন যে সংখ্যাটা এই সেট এ নাই সেটাই হবে বর্তমান স্টেট এর গ্রান্ডি সংখ্যা। একটা উদাহরণ দেখলে ব্যাপারটা পরিস্কার হবে।

মনে করো কোনো একটা স্তুপে ০টা পাথর আছে। আমাদের স্টেট হলো $s=0$। আমরা জানি এটা একটা লুজিং পজিশন, আমরা ধরে নিতে পারি $s=0$ এর জন্য গ্রান্ডি সংখ্যা $g[0]=0$।

যদি স্তপে ১টা পাথর থাকে তাহলে $s=1$। এখান থেকে ১টা পাথর তুলে $s=0$ স্টেট এ যাওয়া যায়। সেট $X$ এ তাহলে আছে $X=\{g[0]\}=\{0\}$। $1$ হলো সর্বনিম্ন সংখ্যা যা $X$ এ নেই, তাহলে আমরা ধরে নিবো $g[1]=1$।

যদি স্তপে ২টা পাথর থাকে তাহলে $s=2$। এখান থেকে ১টা বা ২টা পাথর তুলে $s=1$ বা $s=0$ স্টেট এ যাওয়া যায়। সেট $X$ এ তাহলে আছে $X=\{g[1],g[0]\}=\{0,1\}$। $2$ হলো সর্বনিম্ন সংখ্যা যা $X$ এ নেই, তাহলে আমরা ধরে নিবো $g[2]=2$।

যদি স্তপে ৩টা পাথর থাকে তাহলে $s=3$। এখান থেকে ১টা বা ২টা পাথর তুলে $s=2$ বা $s=1$ স্টেট এ যাওয়া যায়। সেট $X$ এ তাহলে আছে $X=\{g[2],g[1]\}=\{2,1\}$। $0$ হলো সর্বনিম্ন সংখ্যা যা $X$ এ নেই, তাহলে আমরা ধরে নিবো $g[3]=0$।

একই ভাবে হিসাব করলে তুমি পাবে $g[4]=1$, $g[5]=2$ ইত্যাদি।

এখন যদি ৩টা স্তুপে $\{5,2,3\}$ টা পাথর থাকে তাহলে তুমি বলতে পারো গেমটা $\{g[5],g[2],g[3]\}=\{2,2,0\}$ টা পাথর নিয়ে সাধারণ নিম গেম খেলার সমতুল্য। এখন তুমি $xorsum$ দেখে বলতে পারো খেলাটায় কে জিতবে।

গ্রান্ডি সংখ্যা বের করার জন্য সাধারণ সুডোকোড হতে পারে এরকম:

এ পর্যন্ত যদি বুঝে থাকো তাহলে নিচের সমস্যাটা সমাধান করো:

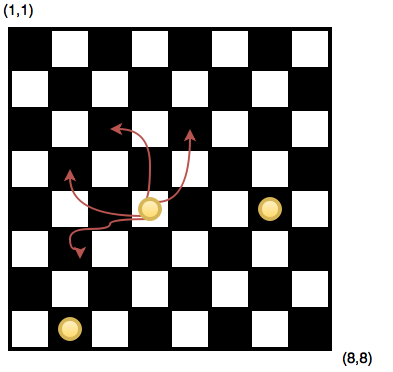
একটা দাবার বোর্ডে $k$ টা কয়েন রাখা আছে। কোনো কয়েন (x,y) ঘরে থাকলে প্রতি চালে কয়েনটিকে (x-2, y+1) অথবা (x-2, y-1) অথবা (x-1, y-2) অথবা (x+1, y-2) ঘরে সরানো যায় , তবে কয়েনটি বোর্ডের বাইরে সরানো যাবে না।

প্রতি চালে বর্তমান খেলোয়াড় উপরের নিয়ম মেনে একটা কয়েন সরাতে পারবে। যে খেলোয়াড় কয়েন সরাতে পারবে না সে হেরে যাবে। তোমাকে কয়েনগুলোর স্থানাংক দেয়া থাকবে, বলতে হবে খেলায় কে জিতবে।

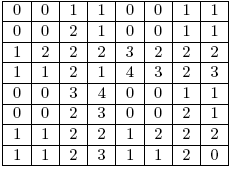
এই দাবার বোর্ডে প্রতিটা ঘরের জন্য গ্রান্ডি সংখ্যা হিসাব করলে তুমি নিচের মতো একটা টেবিল পাবে:

লক্ষ্য করে দেখো যেসব ঘর থেকে অন্য কোনো ঘরে যাওয়া যায় না তাদের গ্রান্ডি সংখ্যা ০, তারমানে সেসব ঘরগুলো হলো লুজিং পজিশন। বাকি ঘরগুলোর জন্য গ্রান্ডি সংখ্যা হিসাব করতে হলে প্রথমে একটা ঘর থেকে অন্য যেসব ঘরে যাওয়া যায় তাদের গ্রান্ডি সংখ্যা হিসাব করতে হবে।  মনে করো সেই সংখ্যাগুলোর সেট হলো $S$। সর্বনিম্ন যে নন-নেগেটিভ সংখ্যা $S$ এ নেই সেটাই হবে বর্তমান ঘরের গ্রান্ডি সংখ্যা।

আজকে এই পর্যন্তই। গ্রান্ডি সংখ্যা কিভাবে নির্ণয় করতে হয় বুঝে থাকলে এই সমস্যাগুলো সমাধান করো। এই পদ্ধতিটা কেন কাজ করে সেটাও চিন্তা করে বের করার চেষ্টা করো।

হ্যাপি কোডিং!