আমরা অনেকেই জানি অয়লার সার্কিট/পাথ কী এবং গ্রাফে অয়লার সার্কিট/পাথ আছে নাকি সেটা কিভাবে বের করতে হয়, কিন্তু গ্রাফে যদি অয়লার সার্কিট/পাথ থেকে থাকে তাহলে সেটা কিভাবে খুজে বের করা যায় সেটা অনেকেই জানিনা। আজকে আমরা সেটাই শিখবো।
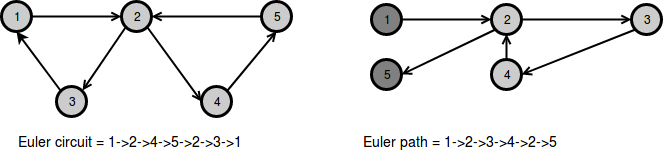
অয়লার সার্কিট এবং পাথ কী সেটা একটু মনে করা নেয়া যাক। অয়লার সার্কিট হলো গ্রাফের এমন একটা পাথ যেটা যে নোডে শুরু হয়েছে সে নোডেই শেষ হয়েছে কিন্তু প্রতিটি এজ ঠিক একবার ব্যবহার করেছে। আর অয়লার পাথ হলো গ্রাফে এমন একটি পাথ যেটা যেকোনো একটি নোডে শুরু হয়ে অন্য একটি নোডে শেষ হয়েছে কিন্তু প্রতিটি এজ ঠিক একবার ব্যবহার করেছে।
- একটি ডিরেক্টেড গ্রাফে অয়লার সার্কিট থাকবে যদি গ্রাফটি কানেক্টেড হয় এবং প্রতিটি নোডের আউটডিগ্রি এবং ইনডিগ্রি সমান হয়।
- একটি আনডিরেক্টেড গ্রাফে অয়লার সার্কিট থাকবে যদি গ্রাফটি কানেক্টেড হয় এবং প্রতিটি নোডের ডিগ্রী জোড় সংখ্যা হয়।
- একটি ডিরেক্টেড গ্রাফে অয়লার পাথ থাকবে শুধুমাত্র যদি গ্রাফটি কানেক্টেড হয় এবং ২টি মাত্র নোডের আউটডিগ্রি এবং ইনডিগ্রির পার্থক্য $1$ হয় এবং বাকি সব নোডের আউটডিগ্রি এবং ইনডিগ্রি সমান হয়। শুরুর নোডের ক্ষেত্রে $indegree = outdegree – 1$ আর শেষের নোডের ক্ষেত্রে $outdegree = indegree – 1$ হবে।
- একটি আনডিরেক্টেড গ্রাফে অয়লার পাথ থাকবে যদি গ্রাফটি কানেক্টেড হয় ২টি মাত্র নোডের ডিগ্রি বিজোড় সংখ্যা হয় (শুরু এবং শেষের নোড) এবং বাকি সব নোডের ডিগ্রি জোড় সংখ্যা হয়।
এখানে ডিরেক্টেড গ্রাফে কানেক্টেড গ্রাফ বলতে বুঝাচ্ছি যদি গ্রাফটিকে আনডিরেক্টেড কল্পনা করো তাহলে প্রতিটি নোড থেকে প্রতিটা নোডে যাবার অন্তত একটি পথ থাকবে।
অয়লার পাথ সমস্যাটি কনিসবার্গ সেতু সমস্যা নামেও পরিচিত, এ ব্যাপারে বিস্তারিত আলোচনা করেছি আমার গ্রাফ অ্যালগরিদম বইয়ে। গ্রাফে অয়লার সার্কিট বা পাথ আছে নাকি সেটা বের করা খুবই সহজ, কিন্তু সার্কিট বা পাথটি খুজে বের করা আরেকটু কঠিন, আজকে সেটা নিয়েই আলোচনা করবো।
অয়লার সার্কিট/পাথ বের করার জন্য একটি পরিচিত অ্যালগরিদম হলো ফ্লিরি’র(Fleury) অ্যালগরিদম। অ্যালগরদিমটি প্রথম প্রকাশিত হয় ১৮৮৩ সালে, বুঝতেই পারছো গ্রাফ থিওরি বয়স কত পুরানো।
ফ্লিরির অ্যালগরিদমটি বুঝতে হলে আমাদের জানতে হবে গ্রাফে ব্রিজ কাকে বলে। আনডিরেক্টেড ব্রিজ হলো এমন এজ যেটা গ্রাফ থেকে মুছে দিলে গ্রাফটি ডিসকানেক্টেড (disconnected) হয়ে যায়। আমরা যখন ডিরেক্টেড গ্রাফ নিয়ে কাজ করবো তখন ব্রিজ খোজার সময় কল্পনা করে নিব গ্রাফটি আনডিরেক্টেড, অর্থাৎ আমরা ‘underlying undirected graph’ থেকে ব্রিজ বের করবো।
গ্রাফে ফ্লিরি’র অ্যালগরিদম অ্যাপ্লাই করার আগে আগে নোডগুলোর ডিগ্রী দেখে জেনে নিতে হবে গ্রাফে অয়লার সার্কিট আছে কি নেই। যদি অয়লার সার্কিট থেকে থাকে তাহলে আমরা যেকোনো নোড থেকে খোজা শুরু করতে পারি, যদি অয়লার পাথ থাকে তাহলে প্রথম নোডটি থেকে শুরু করতে হবে। কিভাবে বুঝবে কোনটা প্রথম নোড? আনডিরেক্টেড গ্রাফে যেকোন নোড ,যার ডিগ্রী বিজোড় সংখ্যা, কে শুরুর নোড ধরে নিতে পারো। ডিরেক্টেড গ্রাফে যে নোডের আউটডিগ্রী ইনডিগ্রীর থেকে ১ বেশি সেটাই অয়লার পাথের শুরুর নোড।
এখন ধরে নিলাম শুরুর নোডটি হলো $u$। এবার আমরা $u$ এর অ্যাডজেসেন্ট যেকোনো একটি নোড $v$ নিব এমন ভাবে যেন $u-v$ এজটি মুছে দিলে গ্রাফটি ডিসকানেন্টেড না হয়ে যায় যায়, অর্থাৎ $u-v$ যেন ব্রিজ না হয়। এরপর $u-v$ এজটা মুছে দিয়ে আমরা পরের নোড $v$ নোড থেকে আবার একই কাজ করবো। কিন্তু এমন হতে পারে যে এমন কোনো এজ $u-v$ নেই যেটা একটি ব্রিজ নয়, সেক্ষেত্রে ব্রিজ ধরেই এগিয়ে যাবো। এভাবে যতক্ষণ না সবগুলো এজ মুছে ফেলা হয় ততক্ষণ আগাতে থাকবো। সবগুলো এজ মুছে ফেলা হয়ে গেলে আমরা অয়লার সার্কিট বা পাথও খুজে পাবো।
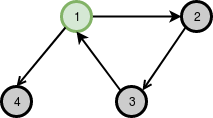
উদাহরণ হিসাবে উপরের গ্রাফটি দেখ। এই গ্রাফে অয়লার সার্কিট নেই কিন্তু পাথ আছে। এখানে $1$ হল শুরুর নোড (ইনডিগ্রি $1$, আউটডিগ্রী $2$) । শুরুতে আমরা দেখতে পাচ্ছি $1->4$ একটি ব্রিজ, আমরা সেটা বাদ দিয়ে $1->2$ ধরে এগিয়ে যাবো এবং এজটি মুছে দিব।
এখন নোড $2$ থেকে একটি মাত্র এজ ধরে যাওয়া যায়, $2->3$ এবং $2->3$ একটি ব্রিজ। যেহেতু আর কোনো অপশন নেই, আমরা $2->3$ ধরেই এগিয়ে যাবো। এভাবে সিমুলেশন করলে দেখা যাবে যে আমাদের পাথ হলো $1->2->3->1->4$। এটাই গ্রাফটির অয়লার পাথ।
অ্যালগরিদমের প্রমাণে যাবো না কিন্তু মূল ধারণাটা হলো একপাশের সবগুলো এজ ঘুরে না আসার আগেই ব্রিজ ভেঙে না দেয়া। তুমি যদি একবার ব্রিজ ভেঙে ফেলো তাহলে গ্রাফটি ডিসকানেক্টেড হয়ে যাবে, তুমি ব্রিজের অন্যপাশের নোডে আর ফিরে আসতে পারবে না। তাই আমরা বুদ্ধি করে আগে সব নন-ব্রিজ ঘুরে আসবো, যখন দেখবো আর সেরকম এজ নাই তখনই শুধু ব্রিজ ভাঙবো।
ফ্লিরি’র অ্যালগরিদম বোঝা সহজ হলেও ইমপ্লিমেন্ট করা কিছুটা ঝামেলার কারণ প্রতিবার এজ মুছে দেয়ার পর ব্রিজ খুজে বের করতে হয়। তুমি যদি প্রতিবার টারজানের ব্রিজ খুজে বের করার অ্যালগরিদম চালাও তাহলে তুমি $E$ বার টারজান অ্যালগরিদম চালাচ্ছো এবং কমপ্লেক্সিটি হয়ে যাচ্ছে $O(E^2)$। তাই আমরা এত ঝামেলায় না গিয়ে অন্য একটি সহজ অ্যালগরিদম ইমপ্লিমেন্ট করবো। তাহলে কেন আমরা ফ্লিরি’র অ্যালগরিদম শিখলাম? কারণ একটা তোমাকে সাইকেল, ব্রিজ, কানেক্টেড কম্পোনেন্ট ইত্যাদি নিয়ে ভাবাবে এবং হয়তো তোমাকে কোনো একদিন অন্য একটা সমস্যা সমাধান করতে সাহায্য করবে।
এখন আমরা শিখবো হেয়ারহলজারের (Heirholzer) অ্যালগরিদম। এই অ্যালগরিদম মূলত অয়লার সার্কিট বের করার জন্য কিন্তু একটু বুদ্ধি খাটিয়ে অয়লার পাথও বের করা যায়, সে কথায় পরে আসছি। একটি গ্রাফে অয়লার সার্কিট থাকলে প্রতিটা নোডের ইনডিগ্রি এবং আউটডিগ্রি সমান হয়। এখন আমাদের পর্যবেক্ষণ শক্তিকে কাজে লাগাতে হবে।
গ্রাফে অয়লার সার্কিট থাকলে প্রতিটা নোড অবশ্যই একটা সাইকেলের অন্তর্গত হতে হবে। প্রতিটা নোড থেকে তুমি যখন বের হবে তখন অবশ্যই একটা সাইকেল ঘুরে সেই নোডে ফিরে আসার পথ থাকবে। এবং সবথেকে গুরুত্বপূর্ণ পর্যবেক্ষণ হলো অয়লার সার্কিট গ্রাফ থেকে একটি সাইকেলের সবগুলো এজ মুছে দিলে বাকি যে কানেক্টেড গ্রাফটি থাকবে সেটা নতুন আরেকটি অয়লার সার্কিট হবে, কারণ যখন তুমি সাইকেলের এজগুলো মুছে দিচ্ছ তখন সাইকেলের অন্তর্ভুক্ত সবগুলো নোডের ইনডিগ্রি এবং আউটডিগ্রি ১ কমছে।
আমাদের কাজ হবে একটা করে সাইকেল ডিটেক্ট করা এবং সাইকেলের এজগুলোকে মুছে ফেলা। কাজটি আমরা রিকার্সিভলি করবো যেন একটি নোড যতগুলো সাইকেলের সাথে যুক্ত সবগুলো সাইকেলের এজ মুছে ফেলা যায়।
|
1 2 3 4 5 6 7 8 9 |
tour_stack = empty stack find_circuit(u): for all edges u->v in G.adjacentEdges(v) do: remove u->v find_circuit(v) end for tour_stack.add(u) return |
উপরের সুডোকোডে কি হচ্ছে বোঝার চেষ্টা করো। এখানে আমরা প্রতিটি নোড থেকে একটি করে এজ মুছে ফেলছি এবং রিকার্সিভলি সেই কম্পোনেন্টের সবগুলো এজ মুছে ফেলছি। সবশেষে নোডটি স্ট্যাকে যোগ করছি। সবকাজ শেষ হওয়ার পর স্ট্যাক থেকে নোডগুলো বের করে নিলেই আমরা অয়লার সার্কিট পেয়ে যাবো।
অ্যালগরিদম বুঝতে সমস্যা হলে বোঝার সবথেকে ভালো উপায় হলো একটি গ্রাফে সিমুলেট করে ফেলা। একবার খাতা-কলমে সিমুলেট করে ফেললেই জিনিসটা পরিস্কার হয়ে যাবে। আমি এখানে সিমুলেশনটা দেখাতে পারতাম, কিন্তু তাহলে তোমার চিন্তা করার অভ্যাস তৈরি হবে না। আশা করি তুমি এটা নিজে নিজে করতে পারবে।
আগে বলেছি এই অ্যালগরিদমটা অয়লার সার্কিট বের করার জন্য, তাহলে অয়লার পাথ কিভাবে বের করা যায়? খুব সহজ, প্রথম নোড থেকে শেষ নোডে একটি ডামি এজ যোগ করে সার্কিট খুজে বের করলেই পাথও পেয়ে যাবে। এই অ্যালগরিদমের কমপ্লিক্সিটি $O(E)$, অ্যালগরিদমটি আনডিরেক্টেড গ্রাফেও কাজ করবে।
মনে করো একজন পোস্টম্যান প্রতিদিন সকালে পোস্টঅফিস থেকে সাইকেল নিয়ে বের হয়ে বিভিন্ন রাস্তায় চিঠি দিয়ে আবার পোস্টঅফিসে ফিরে আসে। কোন পথে গেলে তার সবথেকে কম কষ্ট করতে হবে? যদি রাস্তাগুলোকে একটি গ্রাফ চিন্তা করা হয় এবং গ্রাফটিতে অয়লার সার্কিট থাকে তাহলে এক রাস্তায় কখনোই দুইবার যেতে হবে না। কিন্তু বাস্তবে বেশিভাগ ক্ষেত্রেই সেটা সম্ভব না। সেক্ষেত্রে এক রাস্তা একাধিকবার ব্যবহার করলেও চেষ্টা করা হয় মোট দূরত্ব কমিয়ে আনার। এই প্রবলেমের একটি নাম আছে, এটাকে বলে চাইনিজ পোস্টম্যান প্রবলেম। এটা একটু অ্যাডভান্সড লেভেলের প্রবলেম যেটা সলভ করতে ওয়েটেড বাইপারটাইট ম্যাচিং বা মিন-কস্ট-ম্যাক্স-ফ্লো জানা লাগে। তোমার আগ্রহ থাকলে এই নিয়ে ঘাটাঘাটি করতে পারো।
আজ এ পর্যন্তই, হ্যাপি কোডিং!
প্র্যাকটিস প্রবলেম:
http://www.lightoj.com/volume_showproblem.php?problem=1256
ফেসবুকে মন্তব্য
Powered by Facebook Comments