স্ট্রিং ম্যাচিং: নুথ-মরিসন-প্র্যাট (কেএমপি) অ্যালগরিদম

আজকে আমরা শিখবো কেএমপি (KMP) অ্যালগরিদম ব্যবহার করে স্ট্রিং ম্যাচিং করা। কেএমপি শব্দটি এসেছে ৩জন কম্পিউটার বিজ্ঞানী Donald Knuth, James H. Morris এবং Vaughan Pratt এর নাম থেকে।

আমাদের প্রবলেম হলো একটা দুটি স্ট্রিং text এবং pattern দেয়া আছে, আমাদের বলতে হবে text এর ভিতর pattern স্ট্রিংটি সাবস্ট্রিং হিসাবে আছি কিনা। যেমন ধরো টেক্সটটি হলো “MOD”, এই স্ট্রিংটার ৬টা সাবস্ট্রিং আছে “M”, “O”, “D”, “MO”, “OD” এবং “MOD”, এখন যদি pattern = “MO” খুজতে বলে আমরা true রিটার্ন করবো।

ব্রুটফোর্স অ্যালগরিদম ব্যবহার করে স্ট্রিং ম্যাচিং করার টাইম কমপ্লেক্সিটি $O(n*m)$, যেখানে $n$ এবং $m$ হলো টেক্সট ও প্যাটার্নের দৈর্ঘ্য। কিন্তু কেএমপি ব্যবহার করে $O(n+m)$ কমপ্লেক্সিটিতে প্যাটার্ন খুজে বের করা যায়।

আমরা প্রথমে ব্রুটফোর্স অ্যালগরিদমটা শিখবো এবং শিখতে গিয়ে দেখবো যে আমরা কিছু কাজ বারবার করছি যেটা একটু বুদ্ধিমানের মত চিন্তা করলে করার দরকার নেই। সেখান থেকে আমরা কেএমপি অ্যালগরিদম শিখবো। খাতা-কলম বা হোয়াইট-বোর্ড ছাড়া কেএমপি অ্যালগরিদম ব্যাখ্যা করা আমার জন্য একটু কষ্টকর, তাও আমি চেষ্টা করছি, আশা করি লেখাটা দ্রুত পড়ে ফেলার চেষ্টা না করে ধীরে ধীরে মনযোগ দিয়ে পড়বে।

মনে করো আমাদের টেক্সট হলো “abababacd” এবং প্যাটার্ন হলো “ababac”। ব্রুটফোর্স অ্যালগরিদমে আমরা টেক্সটের প্রতিটা ইনডেক্সে গিয়ে সেখান থেকে লুপ চালিয়ে প্যাটার্ন খুজে বের করার চেষ্টা করি।

bool naive_matching(string text, string pattern) {
  int n = text.size();
  int m = pattern.size();
  for(int i = 0; i < n; i++) { 
    //for each position i in text, we will try 
    //to match text[i, i+1, ..., i+m-1] with pattern[0, 1, ... m-1]
    int j = 0;
    for(j = 0; j < m && i + j < n; j++) { 
      if(text[i + j] != pattern[j]) { 
        break; // mismatch found, break the inner loop
      }
    }
    if(j == m) {
      return true;
    }
  }
  return false;
}

bool naive_matching(string text, string pattern) {

int n = text.size();

int m = pattern.size();

for(int i = 0; i < n; i++) {

//for each position i in text, we will try

//to match text[i, i+1, ..., i+m-1] with pattern[0, 1, ... m-1]

int j = 0;

for(j = 0; j < m && i + j < n; j++) {

if(text[i + j] != pattern[j]) {

break; // mismatch found, break the inner loop

}

if(j == m) {

return true;

}

return false;

}

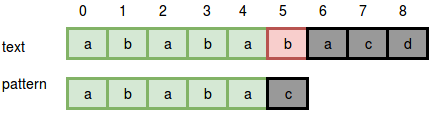
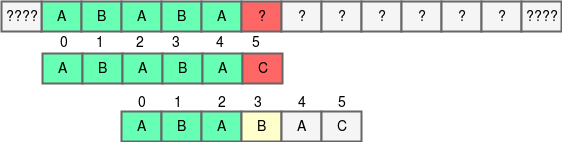
আমরা এই কোডটাকে সিমুলেট করার চেষ্টা করি। শুরুতে i = 0, আমরা টেক্সটের প্রথম ক্যারেক্টার থেকে শুরু করে প্যাটার্ন এবং টেক্সটের একটি একটি করে ক্যারেক্টার মিলাতে থাকবো। যদি সবগুলো ক্যারেক্টার মিলে যায় তাহলে আমরা প্যাটার্ন পেয়ে গেছি। যদি কোনো এক জায়গায় গিয়ে না মিলে তাহলে লুপ ব্রেক করে দিবো। নিচের ছবি দেখ:

চিত্র ১.০

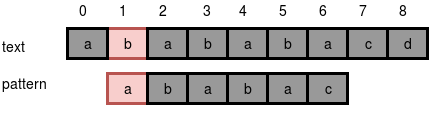
5 নম্বর ক্যারেক্টারে গিয়ে আমরা একটি মিসম্যাচ পেয়েছি। ব্রুট ফোর্স অ্যালগরিদমের ভিতরের লুপটা ৬ নম্বর লাইনে ব্রেক করবে, এরপর ইনডেক্স $i = 1$ এ গিয়ে আবার খুজতে থাকবে।

চিত্র ১.২

এভাবে text এর প্রতিটি ইনডেক্সে গিয়ে লুপ চালিয়ে প্যাটার্ন খুজতে হবে, এজন্য এই অ্যাপ্রোচের টাইম কমপ্লেক্সিটি $O(n*m)$। কোনোভাবে কি আমরা প্রতিটা ইনডেক্সে গিয়ে লুপ চালানো এড়াতে পারি? তার আগে আমাদের জানতে হবে সাফিক্স এবং প্রিফিক্স কি।

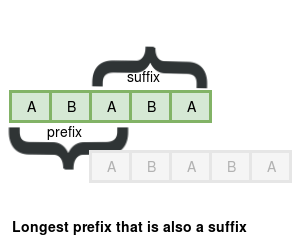
প্রিফিক্স: একটা স্ট্রিং শেষ থেকে শূন্য বা তার বেশি সংখ্যক ক্যারেক্টার ফেলে দিলে যা বাকি থাকে সেটাই একটা স্ট্রিং এর প্রিফিক্স। যেমন “ABC” স্ট্রিং টার প্রিফিক্স হলো “A”, “AB” এবং “ABC”। এর মধ্যে “A” এবং “AB” হলো প্রোপার (Proper) প্রিফিক্স কারণ এগুলো মূল স্ট্রিংটার সমান না।

সাফিক্স: একটা স্ট্রিং শুরু থেকে শূন্য বা তার বেশি সংখ্যক ক্যারেক্টার ফেলে দিলে যা বাকি থাকে সেটাই একটা স্ট্রিং এর সাফিক্স। যেমন “ABC” স্ট্রিং টার সাফিক্স হলো “C”, “BC” এবং “ABC”। এর মধ্যে “C” এবং “BC” হলো প্রোপার (Proper) সাফিক্স কারণ এগুলো মূল স্ট্রিংটার সমান না।

মনে করো আমরা যে প্যাটার্ণটা খুজছি সেটা হলো abxyabcd। এবার নিচের (চিত্র ১.৩) ছবিটা দেখ:

চিত্র ১.৩

ছবিতে (চিত্র ১.৩) আমরা টেক্সটের সাথে প্যাটার্ন মিলাতে মিলাতে এক জায়গায় মিসম্যাচ পেয়েছি। কোন মিসম্যাচ হওয়া ক্যারেক্টারটা কি অথবা তার পরের ক্যারেক্টারগুলো কি সেটা নিয়ে আপাতত চিন্তা করা দরকার নাই। এখন আমরা যদি ব্রুটফোর্সের মতো প্যাটার্নকে একঘর বামে শিফট করে মিলাতে চেষ্টা করি তাহলে আদৌ কি কোন লাভ আছে?

চিত্র ১.৪

১ ঘর যদি শিফট করি তাহলে প্রশ্নবোধক চিহ্নের জায়গাগুলোয় যাই থাকুক না কেন কোনো লাভ নাই। কত ঘর শিফট করলে লাভ হতেও পারে সেটা কিসের উপর নির্ভর করে? সেটা নির্ভর করে প্যাটার্নের যতটুকু প্রিফিক্স টেক্সটের সাথে ম্যাচ করেছে সেটার উপর, এক্ষেত্রে সেই প্রিফিক্সটা হলো “ABXYAB”। আমরা যদি নিচের মত করে শিফট করি তাহলে ম্যাচ পেলেও পেতে পারি:

চিত্র ১.৫

তারমানে আমাদেরকে প্যাটার্নটা এমনভাবে শিফট করতে হবে যাতে প্যাটার্নের প্রিফিক্সের সাথে প্যাটার্নেরই সাফিক্সের ‘আংশিক’ (partial) ম্যাচিং পাই। তাহলে যেটা ঘটবে, আমরা প্যাটার্নের প্রিফিক্সের সাথে ইনপুট টেক্সটের partial ম্যাচ পাবো এবং এরপর আমরা আবার সামনে গিয়ে ক্যারেক্টার বাই ক্যারেক্টার মিলিয়ে দেখবো পুরো টেক্সটা ম্যাচ করে নাকি।

আরেকটা উদারহরণ দেখলে পরিষ্কার হবে। মনে করো এবার প্যাটার্নটা হলো “ABABAC” এবং আমরা নিচের মতো আংশিক ম্যাচিং পেয়েছি:

চিত্র ১.৬

এবার আমরা কতটুকু শিফট করবো সেটা নির্ভর করবে ম্যাচ করা প্রিফিক্স “ABABA” এর উপর। নিচের ছবিটা দেখো:

চিত্র ১.৭

চিত্র ১.৭ এ প্যাটার্নটা ডানে ২ ঘর শিফট করেছি। এতে করে আমরা প্যাটার্নের প্রিফিক্সের সাথে প্যাটার্নেরই সাফিক্সের আংশিক ম্যাচ পাবো। এক্ষেত্রে প্যাটার্নের প্রথম ৩ ক্যারেক্টারের সাথে শেষ ৩ ক্যারেক্টার ম্যাচ করছে। তারমানে টেক্সটের সাথেও প্যাটার্নের প্রথম ৩ ক্যারেক্টার ম্যাচ করবে। এরপর আমরা আবার সামনে গিয়ে বাকি ক্যারেক্টারগুলো মিলিয়ে দেখবো।

এখন ধরো দূর্ভাগ্যক্রমে আমরা আবার মিসম্যাচ পেলাম:

চিত্র ১.৮

এখন কতখানি শিফট করবো? সেটা নির্ভর করে “ABA” এর উপর। আমাদেরকে এমনভাবে ABA কে এমনভাবে ডানে শিফট করতে হবে যেন শিফট করার পর ABA এর প্রিফিক্সের সাথে ABA এর সাফিক্স আংশিক ম্যাচ করে। এক্ষেত্রে চিত্র ১.৯ এর মত করে শিফট করতে হবে:

চিত্র ১.৯

এতগুলো উদাহরণ দেয়ার উদ্দেশ্য একটা জিনিস পরিষ্কার করা, প্যাটার্নের কতখানি প্রিফিক্স টেক্সটের সাথে ম্যাচ করেছে তার উপর নির্ভর করবে প্যাটার্ন কয়ঘর শিফট করবো তার উপর নির্ভর করবে প্যাটার্ন কয়ঘর শিফট করবো।

মনে করো যতখানি প্রিফিক্স ম্যাচ করেছে সেই স্ট্রিংটুকুর নাম $P$। $P$ কতঘর শিফট করলে আমরা “যে টেক্সটটুকু অলরেডি ম্যাচ করেছে তার সাফিক্সের সাথে” আংশিক ম্যাচ পাবো?

সেটা জানতে আমাদের বের করতে হবে $P$ স্ট্রিংটার সবথেকে বড় প্রিফিক্স যেটা একই সাথে $P$ এর একটা সাফিক্স ও। এই লাইনটা শুনলে আমার নিজেরই তালগোল পাকিয়ে যায়, তাই আসো আরেকটা ছবি দেখি:

চিত্র ১.১০

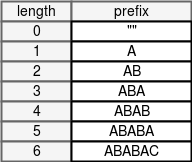
আশা করি ছবি দেখে পরিষ্কার হয়েছে লাইনটির মানে। সর্বোচ্চ কতখানি সাফিক্স প্রিফিক্সের সাথে মিলে যায় সেটা বের করে শিফট করতে হবে। “ABABAC” স্ট্রিং এর প্রিফিক্স আছে ৭টা:

চিত্র ১.১১

এবার সবগুলো স্ট্রিং এর জন্য সবথেকে বড় প্রিফিক্সের দৈর্ঘ্য বের করবো যেটা একই সাথে একটা সাফিক্স। এক্ষেত্রে যেহেতু আমাদের আংশিক ম্যাচ দরকার, আমরা শুধুমাত্র প্রোপার সাফিক্স ও প্রিফিক্স নিয়ে চিন্তা করবো (অর্থাৎ সাফিক্স/প্রিফিক্সের দৈর্ঘ্য হবে স্ট্রিংটার থেকে কম)।

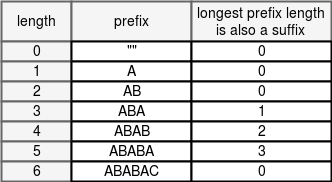kmp-Page-16(1) চিত্র ১.১২

এই টেবিলটির একটা নাম আছে, এটাকে বলা হয় Failure table (ফেইলর টেবিল)। এই টেবিল দেখে আমরা বলে দিতে পারি প্যাটার্নের কতখানি প্রিফিক্স ম্যাচ করার পর মিসম্যাচ পাওয়া গেলে আবার কোথা থেকে ম্যাচিং শুরু করতে হবে।

চিত্র ১.১৩

যেমন উপরের ABABA পর্যন্ত ম্যাচ করার পর একটা ফেইলড ম্যাচ পেয়েছি। চিত্র ১.১২ এর টেবিলের ৬নম্বর রো থেকে পাই যে প্যাটার্নের প্রথম ৩ ক্যারেক্টার নিয়ে যে প্রিফিক্স হয় সেটা প্যাটার্নের শেষ ৩ক্যারেক্টার নিয়ে যে সাফিক্স হয় তার সমান। তারমানে প্যাটার্নের প্রথম ৩ ক্যারেক্টার “যে টেক্সটটুকু অলরেডি ম্যাচ করেছে” তার সাফিক্সের সমান। তাহলে আমরা প্যাটার্নের প্রথম ৩ক্যারেক্টার বাদ দিয়ে পরের ক্যারেক্টার থেকে আবার ম্যাচিং শুরু করবো।

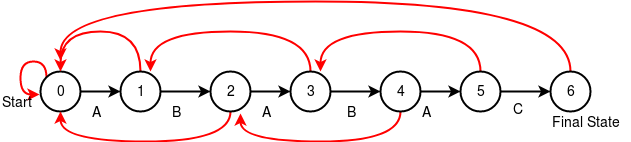
তুমি যদি থিওরি অফ কম্পিউটেশনের কোনো কোর্স করে থাকো তাহলে বুঝতে পারছো ফেইলর টেবিলটা আসলে এক ধরনের “ফাইনাইট স্টেট অটোমাটা” (না পড়ে থাকলেও চিন্তার কিছু নেই)। অটোমেশন হলো একটা “সেট অফ স্টেট (set of states)” এবং এক স্টেট থেকে অন্য স্টেট এ কিভাবে যেতে হবে সেরকম কিছু নিয়ম। আমাদের ক্ষেত্রে স্টেট হলো প্যাটার্নের কতখানি ম্যাচ করেছে সেটা। আর এক স্টেট থেকে অন্য স্টেটে কিভাবে যাবো সেটা নির্ভর করে টেক্সট এবং প্যাটার্নের পরবর্তী ক্যারেক্টার ম্যাচ করছে নাকি তার উপর। যদি ম্যাচ করে তাহলেতো সহজ, পরের ক্যারেক্টারে গিয়ে আবার ম্যাচ করার চেষ্টা করবো। আর যদি ম্যাচ না করে তাহলে কতখানি সাফিক্স প্রিফিক্সের সাথে মিলে গিয়েছে (চিত্র ১.১০) সেটা বের করবো ফেইলর টেবিল দেখে। সহজে বোঝার জন্য আমরা ফেইলর টেবিলটাকে নিচের মত করে আকতে পারি:

চিত্র ১.১৪

চিত্র ১.১৪ এ আমরা ABABAC স্ট্রিং এর জন্য অটোমেশনটাকে দেখতে পাচ্ছো। Start স্টেট হলো যখন কোনো ক্যারেক্টার ম্যাচ করেনি। প্রতিবার একটা করে ক্যারেক্টার ম্যাচ করলে আমরা কালো এজ দিয়ে পরের স্টেটে যাবো, ফাইনাল স্টেটে চলে গেলে কাজ শেষ। লাল তীর চিহ্ন দিয়ে দেখানো হয়েছে মিসম্যাচ পেলে কোন স্টেট এ যাবো। চিত্র ১.১২ এর টেবিলের সাথে মিলালে বুঝবে ফেইলর টেবিল আর উপরের গ্রাফটি আসলে একই জিনিস বুঝাচ্ছে।

এখন আমাদের হাতে ২টি সমস্যা, প্রথমটা হলো ফেইলর টেবিলটা তৈরি করা, ২য়টি হলো সেটা ব্যবহার করে ম্যাচিং করা।

প্রথমে আমরা ফেইলর টেবিলটা তৈরি করি। আমরা এমন একটি ফাংশন লিখবো যেটা $failure[]$ নামের m সাইজের একটা অ্যারে তৈরি করবে, “ABABAC” স্ট্রিং এর জন্য অ্যারেটা হবে এরকম:

$failure[0] = 0$
$failure[1] = 0$
$failure[2] = 0$
$failure[3] = 1$
$failure[4] = 2$
$failure[5] = 3$
$failure[6] = 0$

এখানে ইনডেক্সিং নিয়ে একটু সাবধানে থাকতে হবে। failure[i] দিয়ে আমরা স্ট্রিং এর i নম্বর ইনডেক্সের কথা বুঝাচ্ছি না, বরং $i$ দৈর্ঘ্যের প্রিফিক্সের কথা বুঝাচ্ছি।

এখন মনে করো $i$ দৈর্ঘ্যের প্রিফিক্সের জন্য $failure[i]$ এর মান আমি জানি না কিন্তু $0 <= i <= length$ পর্যন্ত সব দৈর্ঘ্যের জন্য আমি failure[length] এর মান আগেই কোনোভাবে বের করে ফেলেছি। এখন আমি দেখবো $i – 1$ দৈর্ঘ্যের স্ট্রিং এর জন্য কতখানি ম্যাচ পেয়েছি এবং বর্তমানে যে ক্যারেক্টারে আছি সেটা ব্যবহার করে ম্যাচটাকে লম্বা করা যায় নাকি।

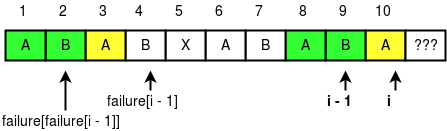
চিত্র ১.১৫ এ একটা উদাহরণ দেখানো হয়েছে:

চিত্র ১.১৫

চিত্র ১.১৫ এ আমরা $failure[10]$ এর মান বের করার চেষ্টা করছি। আমরা আগের ক্যারেক্টারের গিয়ে $failure[i – 1]$ এর মান দেখে বুঝবো কতটুকু প্রিফিক্স-সাফিক্স অলরেডি ম্যাচ করেছে। এরপর চেষ্টা করবো পরের ক্যারেক্টারের সাথে বর্তমান ক্যারেক্টারকে মিলানোর (চিত্র ১.১৫ এ হলুদ রঙ এর ঘর)। যদি মিলে যেত তাহলে $failure[10]$ এর মান হতো $failure[9] + 1 = 4 + 1 = 5$। কিন্তু যেহেতু মিলেনি, আমরা পরবর্তি সেরা ম্যাচিং এ চলে যাবো এবং সেটা পাবো $failure[failure[i-1]]$ এ:

চিত্র ১.১৬

এবার হলুদ ঘরের ক্যারেক্টার দুটো মিলে গেছে, তারমানে $i = 10$ এর জন্য “ABA” সাফিক্স এবং প্রিফিক্স ম্যাচ করে যার দৈর্ঘ্য $3$, তাই $failure[10]$ এর মান হবে $3$।

আমাদের বেস কেস হবে, $failure[0] = failure[1] = 0$। বাকি $2 <= i <= length$ এর জন্য failure[i] মান আমরা আগেরগুলো দেখে দেখে বের করতে পারবো। নিচের কোডটা দেখো:

//https://www.topcoder.com/community/data-science/data-science-tutorials/introduction-to-string-searching-algorithms/
#define MAX 100000
int failure[MAX];

void build_failure_function(string pattern, int m) {
  failure[0] = 0 
  failure[1] = 0; //base case
  
  for(int i = 2; i <= m; i++) {  //i is length of the prefix we are dealing with
    // j is the index of the largest next partial match 
    // (the largest suffix/prefix) of the string under index i - 1
    int j = failure[i - 1];
    while(true) {
      // check if the last character of prefix of length i "expands" the current "candidate"
      if(pattern[j] == pattern[i - 1]) { 
        failure[i] = j + 1; 
        break; 
      }
      // if we cannot "expand" even the empty string
      if(j == 0) { 
          failure[i] = 0; 
          break; 
      }
      // else go to the next best "candidate" partial match
      j = failure[j];
    }
  }   
}

//https://www.topcoder.com/community/data-science/data-science-tutorials/introduction-to-string-searching-algorithms/

#define MAX 100000

int failure[MAX];

void build_failure_function(string pattern, int m) {

failure[0] = 0

failure[1] = 0; //base case

for(int i = 2; i <= m; i++) { //i is length of the prefix we are dealing with

// j is the index of the largest next partial match

// (the largest suffix/prefix) of the string under index i - 1

int j = failure[i - 1];

while(true) {

// check if the last character of prefix of length i "expands" the current "candidate"

if(pattern[j] == pattern[i - 1]) {

failure[i] = j + 1;

break;

}

// if we cannot "expand" even the empty string

if(j == 0) {

failure[i] = 0;

break;

}

// else go to the next best "candidate" partial match

j = failure[j];

}

ফেইলর টেবিল জেনারেট করা হয়ে গেলে আমরা স্ট্রিং ম্যাচিং শুরু করতে পারি। কোড লেখার আগে তুমি একবার অটোমেশন গ্রাফটা একে হাতে কলমে সিমুলেট করো। আমাদের দুইটা পয়েন্টার থাকবে $i$ এবং $j$। $i$ দিয়ে বুঝাবো আমরা অটোমেশনের কোন স্টেট এ আছি, অর্থাৎ কতখানি প্রিফিক্স অলরেডি ম্যাচ করেছে এবং $j$ দিয়ে বুঝাবো টেক্সটের কোন ক্যারেক্টারটার সাথে ম্যাচ করছি। যদি $text[j] == pattern[i]$ হয় তাহলে আমরা $i$ এবং $j$ এর মান ইনক্রিমেন্ট করে আবার ম্যাচ করার চেষ্টা করবো, অর্থাৎ অটোমেশনের কালো তীরচিহ্ন ধরে আগাবো (চিত্র ১.১৪)। কিন্তু যদি $text[j] != pattern[i]$ হয় তাহলে আমরা ফেইলর টেবিল ব্যবহার করে যতটুকু সাফিক্স-প্রিফিক্স ম্যাচ করেছে সেখান থেকে আবার ম্যাচিং শুরু করবো, অর্থাৎ $i = failure[i]$ হয়ে যাবে। আর যদি দেখি $i = 0$ হয়ে গেছে কিন্তু আমরা এখনোও ম্যাচ করতে পারছি না তাহলে $j$ এর মান ইনক্রিমেন্ট করে টেক্সটের পরের ক্যারেক্টার থেকে আবার ম্যাচিং শুরু করতে হবে।

bool kmp(string text, string pattern)
{
  int n = text.size();
  int m = pattern.size();
  build_failure_function(pattern, m); 

  int i = 0; // the initial state of the automaton is
         // the empty string

  int j = 0; // the first character of the text
  
  while(true) {
    if(j == n) {
        return false; //reached the end of the text
    }

    // character matched
    if(text[j] == pattern[i]) {
      i++; // change the state of the automaton
      j++; // get the next character from the text
      if(i == m) {
          return true;
      }
    } else {
        if (i == 0) {
            // if we reached the empty string and failed to
            // "expand" even it; we go to the next 
            // character from the text, the state of the
            // automaton remains zero
            j++;
        }
        else {
             //we try to "expand" the next best (largest) match
            i = failure[i];
        }
    }
  }
  return false;
}

bool kmp(string text, string pattern)

{

int n = text.size();

int m = pattern.size();

build_failure_function(pattern, m);

int i = 0; // the initial state of the automaton is

// the empty string

int j = 0; // the first character of the text

while(true) {

if(j == n) {

return false; //reached the end of the text

}

// character matched

if(text[j] == pattern[i]) {

i++; // change the state of the automaton

j++; // get the next character from the text

if(i == m) {

return true;

}

} else {

if (i == 0) {

// if we reached the empty string and failed to

// "expand" even it; we go to the next

// character from the text, the state of the

// automaton remains zero

j++;

}

else {

//we try to "expand" the next best (largest) match

i = failure[i];

}

return false;

}

কেএমপি অ্যালগরিদমের টাইম কমপ্লেক্সিটি O(n + m)। লিনিয়ার টাইম স্ট্রিং ম্যাচিং করার আরেকটা অ্যালগরিদম রবিন-কার্প নিয়ে আগে লিখেছিলাম। কিন্তু হ্যাশ কলিশনের জন্য রবিন-কার্পের পারফরমেন্স অনেক ক্ষেত্রেই খারাপ হয়ে যেতে পারে, বেশিভাগ ক্ষেত্রেই কেএমপি ব্যবহার করে ম্যাচিং করা সুবিধাজনক।

প্রোগ্রামিং কনটেস্টে সরাসরি কেএমপি ব্যবহার করে সমাধান করতে হয় এমন সমস্যা খুব বেশি পাবে না, কিন্তু ফেইলর ফাংশনের প্রোপার্টি ব্যবহার করে সমাধান করতে হয় এমন সমস্যা প্রায়ই পাওয়া যায়। পরবর্তি কোনো একটা লেখায় সেরকম কিছু সমস্যা নিয়ে আলোচনা করবো। আপাতত এই পর্যন্তই, হ্যাপি কোডিং!

প্র্যাকটিস প্রবলেম:

http://www.lightoj.com/volume_showproblem.php?problem=1255
http://www.lightoj.com/volume_showproblem.php?problem=1258

রিসোর্স:

https://www.topcoder.com/community/data-science/data-science-tutorials/introduction-to-string-searching-algorithms/

ফেসবুকে মন্তব্য

comments

শাফায়েতের ব্লগ

স্ট্রিং ম্যাচিং: নুথ-মরিসন-প্র্যাট (কেএমপি) অ্যালগরিদম

ফেসবুকে মন্তব্য

Leave a Reply Cancel reply