স্কয়ার-রুট ডিকম্পোজিশন টেকনিক ব্যবহার করে বেশ কিছু প্রবলেমের টাইম কমপ্লেক্সিটি $O(Sqrt(n))$ এ নামিয়ে আনা যায়। একটা উদাহরণ দিয়ে শুরু করি। ধরা যাক তোমাকে একটা ইন্টিজার অ্যারে দেয়া আছে এবং কিছু অপারেশন দেয়া আছে। অপারেশন দুই ধরণের হতে পারে, একটা হলো $[l, r]$ ইনডেক্সের ভিতর সবগুলো সংখ্যার যোগ ফল বের করতে হবে, অন্যটা হলো i তম ইনডেক্সের মান আপডেট করতে হবে। অনেকে হয়তো সেগমেন্ট ট্রি বা বাইনারি ইনডেক্সড ট্রি ব্যবহার করে এটা সমাধান করতে পারবে। আজকে আমরা এটা সমাধান করার আরেকটা নতুন পদ্ধতিতে শিখবো।
একেবারেই সাধারণ পদ্ধতিতে আমরা কি করবো? প্রতিবার যোগফল বের করতে বললে $[l, r]$ রেঞ্জে একটা লুপ চালিয়ে যোগফল বের করবো এবং আপডেট অপারেশন শুধু $i$ তম ইনডেক্সটা আপডেট করে দিবো। সেক্ষেত্রে যোগফল বের করার কমপ্লেক্সিটি হচ্ছে $O(n)$।
এখন আমরা চেষ্টা করবো অ্যারেটাকে কিছু সেগমেন্টে ভাগ করে ফেলতে। এরপর যোগফল বের করার সময় প্রতিটা সেগমেন্টের যোগফল বের করলেই হবে। নিচের ছবিটা দেখো:
আমাদের অ্যারের সাইজ ছিলো $13$। আমরা এমন ভাবে ভাগ করত চাই যেন প্রতিটা সেগমেন্টের সাইজ প্রায় এক হয় এবং সেগমেন্টের সাইজ এবং সেগমেন্ট সংখ্যা প্রায় একই হয়। $13$ এর স্কয়ার রুট হলো $3.61 ~ 3$। আমরা যদি অ্যারেটাকে $3$ সাইজের সেগমেন্টে ভাগ করি তাহলে আমরা $13/3 = 4$ টা সেগমেন্ট পাবো, শেষের সেগমেন্ট ছাড়া প্রতিটার আকার $3$।
অ্যারের সাইজ যদি নিজে একটা স্কয়ার নাম্বার না হয় তাহলে আমরা একটা সেগমেন্ট বেশি পাবো এবং শেষের সেগমেন্টের সাইজ একটু কম হবে, সেটা তেমন কোনো সমস্যা না। কেন এভাবে ভাগ করলে সুবিধা সেটা আমরা একটু পরেই বুঝবো।
এবার আমাদেরকে যদি $[l, r]$ রেঞ্জে কুয়েরি করতে বলে তাহলে আমরা শুধু দেখবো কোন কোন সেগমেন্ট আমাদের রেঞ্জের ভিতর পড়ছে এবং সেই রেঞ্জ গুলোর যোগফল বের করবো।
শুরুতে আমাদেরকে সেগমেন্ট গুলো প্রি-প্রসেস করে নিতে হবে। নিচের কোডটি দেখো:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
int segment[10000]; int preprocess(int input[], int n) { int current_segment = -1; int segment_size = sqrt(n); for (int i=0; i<n; i++) { if (i % segment_size == 0) { current_segment++; //new segment } segment[current_segment] += input[i]; } return segment_size; } |
আমরা ইনপুট অ্যারেকে ট্র্যাভার্স করছি এবং যতবার $i % segment_size == 0$ হচ্ছে ততবার পরের সেগমেন্টে চলে যাচ্ছি।
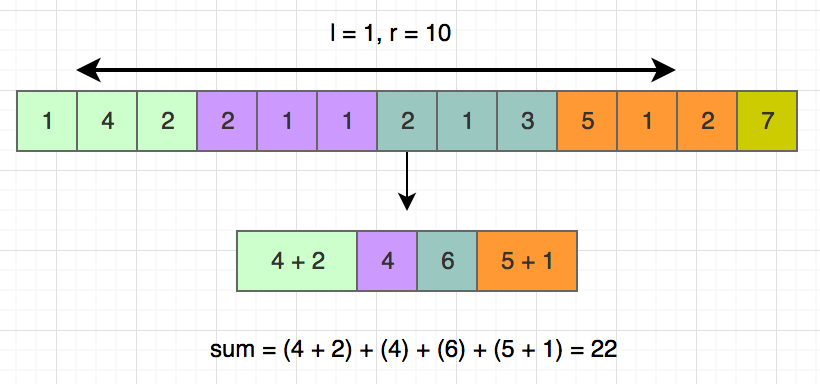
$[1, 10]$ রেঞ্জের জন্য কোন কোন সেগমেন্টের যোগফল বের করতে হবে সেটা পরের ছবিতে দেখানো হয়েছে।
ঝামেলা হলো সবগুলো সেগমেন্ট পুরোপুরি আমাদের রেঞ্জের ভিতর পড়েনি। প্রথম এবং শেষ সেগমেন্ট যদি পুরোপুরি রেঞ্জ টাকে কভার না করে তাহলে সেই দুটি সেগমেন্টের জন্য আমাদের লুপ চালিয়ে যোগফল বের করতে হবে। আমাদের সেগমেন্ট আছে $sqrt(n)$ টা, আবার প্রতিটা সেগমেন্টের আকারও $sqrt(n)$, সর্বোচ্চ দুটি সেগমেন্টে লুপ চালাতে হবে, তাই কুয়েরির মোট কমপ্লেক্সিটি থাকছে $sqrt(n)$। এইজন্য আমরা সেগমেন্ট সংখ্যা এবং সেগমেন্টের আকার যতটা সম্ভব কাছাকাছি রেখেছি।
এখন ছোট একটি প্রশ্ন। কোনো একটা ইনডেক্স i এর জন্য কিভাবে বুঝবে i কোন সেগমেন্টে অবস্থিত? খুব সহজ, $i/segment_size$ এর মান দেখেই বোঝা যাবে।
নিচের কোডে দেখিয়েছি কিভাবে কুয়েরি করতে হবে:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
int query(int input[], int segment_size, int l, int r) { int sum = 0; //loop the first segment //until we reach r or a starting index while (l < r && l % segment_size != 0) { sum += input[l]; l++; } //Loop until we reach //segment that contains r while (l + segment_size <= r) { sum += segment[l / segment_size]; l += segment_size; } //loop until r while (l<=r) { sum += input[l]; l++; } return sum; } |
কুয়েরি কে আমরা ৩ ভাগে ভাগ করেছি যেটার কথা একটু আগেই আলোচনা করেছি।
সবশেষে আপডেট। আপডেট খুবই সহজ, $i$ তম ইনডেক্স আপডেট করতে হলে $i$ কোন সেগমেন্টে আছে সেটা বের করে সেটার যোগফল আপডেট করে দিলেই হচ্ছে।
|
1 2 3 4 5 6 7 |
void update(int input[], int segment_size, int i, int val) { int segment_no = i / segment_size; segment[segment_no] -= input[i]; segment[segment_no] += val; input[i] = val; } |
আপডেট করার কমপ্লেক্সিটি O(1)।
এটাতো গেলো খুবই সহজ একটা প্রবলেম। এই টেকনিক ব্যবহার করে ট্রি এর LCA ও বের করা যায়, সেটা শিখতে হলে এই লিংকটা দেখতে পারো। আর যারা একটু অ্যাডভান্সড লেভেলে তারা এই পিডিএফ টা দেখতে পারো।
হ্যাপি কোডিং!
এই লেখাটি আমি ইংরেজিতেও অনুবাদ করেছি, যদি পড়তে চাও তাহলে এখানে ক্লিক করো।
ফেসবুকে মন্তব্য
Powered by Facebook Comments