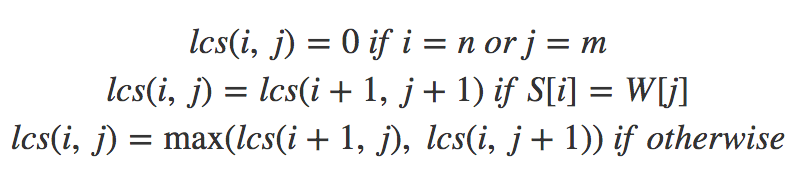আগের পর্ব গুলোতে আমরা যেসব প্রবলেম দেখে এসেছি সেগুলোর সাবপ্রবলেমের স্টেট ছিল মাত্র ১টা। এইবার আমরা আরেকটু জটিল সমস্যা সমাধান করবো যার নাম লংগেস্ট কমন সাবসিকোয়েন্স বা LCS। এটা শেখার পরে আমি এডিট ডিসটেন্স প্রবলেম নিয়ে অল্প কিছু কথা বলবো এবং তোমার কাজ হবে সেটা নিজে নিজে সমাধান করা।
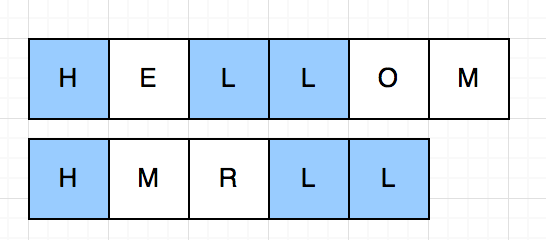
এই প্রবলেমে তোমাকে দুটি স্ট্রিং দেয়া থাকবে $S$ এবং $W$। তোমাকে তাদের মধ্যে লংগেস্ট কমন সাবসিকোয়েন্স এর দৈর্ঘ্য বের করতে হবে। সাবসিকোয়েন্সের সংজ্ঞাটা মনে করিয়ে দেই, একটা স্ট্রিং থেকে কিছু ক্যারেক্টার মুছে দিলে যা বাকি থাকে সেটাই স্ট্রিংটা সাবসিকোয়েন্স। একটা স্ট্রিং এর $2^{n}$ টা সাবসিকোয়েন্স থাকতে পারে। নিচের ছবিতে দুটি স্ট্রিং এবং তাদের লংগেস্ট কমন সাবসিকোয়েন্স দেখানো হয়েছে।
LCS এর দৈর্ঘ্য এক্ষেত্রে $3$।
আমাদের প্রবলেমটা হলো $S$ এবং $W$ এর LCS বের করতে হবে। আমরা $S$ এর ইনডেক্সগুলো হলো $i$ এবং $W$ এর ইনডেক্স $j$ দিয়ে প্রকাশ করবো। এখন নিচ
এখন আমরা এভাবে চিন্তা করতে পারি, শুরুতে আমরা দুটি স্ট্রিং এরই প্রথম ইনডেক্স $i = 0$ এবং $j = 0$ তে আছি এবং আমাদেরকে $lcs(0, 0)$ বের করতে হবে। এখন আমরা যদি যেকোনো $(i, j)$ এর জন্য $lcs(i, j)$ বের করতে পারি তাহলেই কিন্তু আমাদের কাজ হয়ে যায়। $lcs(i, j)$ বলতে বুঝাচ্ছে $i$ এবং $j$ তম ইনডেক্স থেকে শুরু হওয়া $S$ এবং $W$ এর সাফিক্সের LCS। যেমন $lcs(1,2)$ হলো “ELLOM” এবং “RLL” এর LCS।
এখন আমরা যখন $(i, j)$ তে আছি তখন ৩টি ঘটনা ঘটতে পারে:
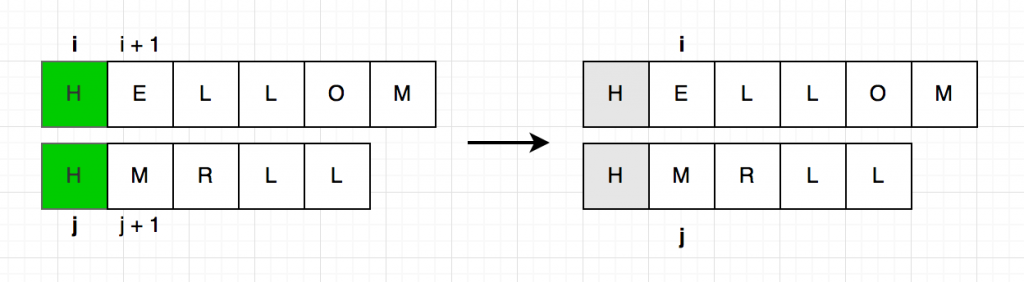
- $S[i] = W[j]$, অর্থাৎ দুটি স্ট্রিং এই একই ক্যারেক্টার আছে। সেক্ষেত্রে ওই ক্যারেক্টারটাকে LCS এর অংশ ধরে নিয়ে আমরা বাকি সাফিক্সটুকুর LCS বের করতে পারি। তারমানে এখন আমাদের $lcs(i + 1, j + 1)$ প্রবলেমটা সলভ করতে হবে, এখানে অনুমান করার কোনো ব্যাপার নেই।
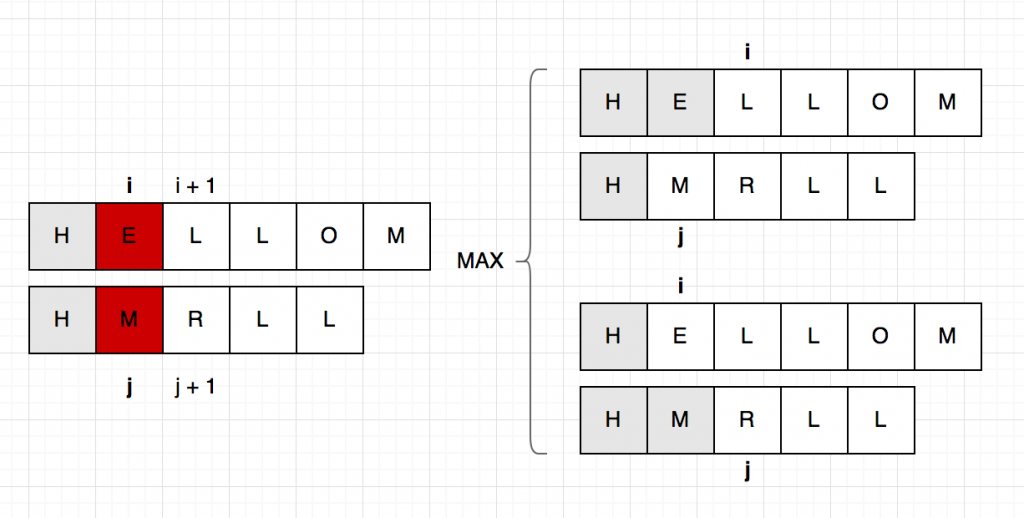
- $S[i] \ne W[j]$ হলে ব্যাপারটা আরেকটু ইন্টারেস্টিং। যেহেতু ক্যারেক্টার দুটি মিলছে না, অন্তত একটা ক্যারেক্টার আমাদের ফেলে দিতে হবে। এখন আমাদের হাতে দুটি চয়েজ, $i$ তম ইনডেক্সটা ফেলে দিয়ে $lcs(i + 1, j)$ ক্যালকুলেট করা, অথবা $j$ তম ইনডেক্সটাকে ফেলে দিয়ে $lcs(i, j + 1)$ ক্যালকুলেট করা। বুঝতেই পারছো আমরা দুটি পথে গিয়ে ম্যাক্সটাকে বেছে নিবো।
- $i = n$ বা $j = m$ হয়ে যাওয়া মানে কোন একটা স্ট্রিং এর শেষ মাথায় চলে গেছি, সেক্ষেত্রে $0$ রিটার্ন করতে হবে।
আমরা আমাদের রিকার্সিভ ফর্মুলা তাহলে পেয়ে গিয়েছি:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
#define MAX_LEN 20 #define EMPTY_VALUE -1 int mem[MAX_LEN][MAX_LEN]; int lcs(int i,int j, string &S, string &W) { if(i == S.size() || j == W.size()) return 0; if(mem[i][j] != EMPTY_VALUE) { return mem[i][j]; } int ans=0; if(S[i] == W[j]) { ans = 1 + lcs(i + 1,j + 1, S, W); } else{ int val1 = lcs(i + 1, j, S, W); int val2 = lcs(i,j + 1, S, W); ans=max(val1,val2); } mem[i][j] = ans; return mem[i][j]; } |
কমপ্লেক্সিটি:
আমাদের স্টেট হলো $(i, j)$ যেখানে $i$ এর মান হতে পারে $[0, n-1]$ এর মধ্যে এবং $j$ হতে পারে $[0, m – 1]$ এর মধ্যে। তাহলে মোট স্টেট আছে $n * m$ টা এবং রিকার্সনের ভিতর আমরা বাকি যেসব কাজ করেছি সেগুলো কমপ্লেক্সিটি কনস্টেন্ট। তাহলে মোট কমপ্লেক্সিটি হবে $O(n * m)$, জেনারেলাইজ করে বলা যায় $O(n^{2})$।
ইটারেটিভ ভার্সন:
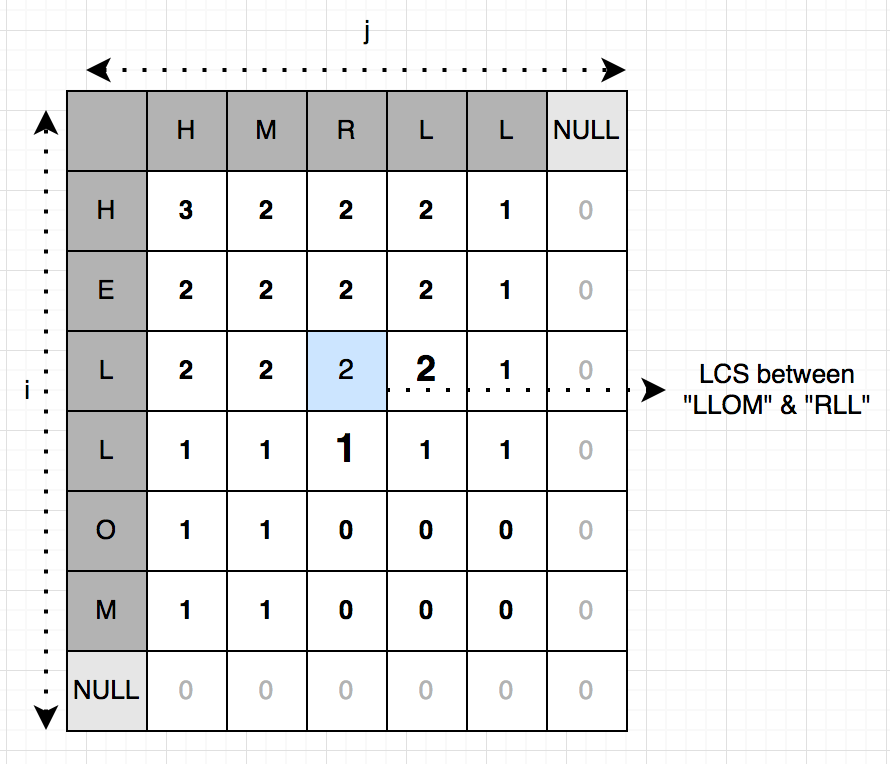
ইটারেটিভ ভার্সন লেখার জন্য আমাদেরকে বুঝতে হবে স্টেটগুলো কোন অর্ডারে আপডেট হচ্ছে (টপোলজিকাল অর্ডার)। আমরা একটু mem টেবিলটার দিকে তাকাই:
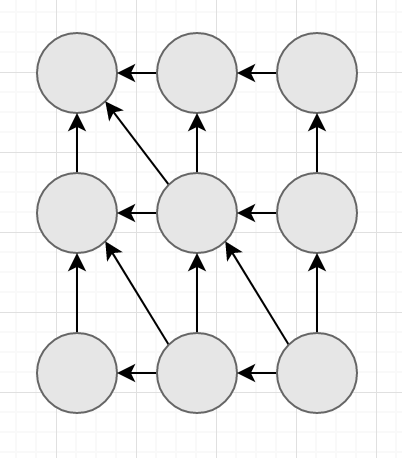
রিকার্সিভ ভার্সনে এই টেবিলটা তৈরি হয়েছে $lcs(0, 0)$ কল করার পর (শেষ রো এবং কলাম টেবিলের অংশ না, দেখানো হয়েছে বোঝার সুবিধার জন্য)। এই টেবিলের প্রতিটি সেল $(i, j)$ আপডেট হয়েছে হয় তার ডান কোনার সেল $(i + 1, j + 1)$ থেকে অথবা উপর বা নিচের সেল $(i, +1, j)$, $(i, j + 1)$ থেকে। তো তুমি প্রতিটা সেলকে গ্রাফের একটা নোড হিসাবে কল্পনা করলে সেটা এরকম দেখাবে
বোঝা যাচ্ছে নিচের ডান কোনার সেল $(n-1, m-1)$ থেকে শুরু করে আমাদেরকে টেবিলটা পূরণ করতে হবে। আমরা সেটা চাইলে row by row করতে পারি। এখন আমার সাজেশন হবে উপরের উদাহরণটার জন্য তুমি হাতে-কলমে একবার টেবিলটা তৈরি করো, তাহলেই জিনিসটা মাথায় গেথে যাবে।
আমরা যদি এরকম ভাবে নেস্টেড লুপ চালাই তাহলে টপোলজিকাল অর্ডারে সেলগুলোকে পাবো:
|
1 2 3 4 5 |
for (int i = n - 1; i >= 0;i--) { for (int j = m - 1; j>=0; j--) { //TODO: update table } } |
ইটারেটিভ ডিপিতে বেস-কেস হ্যান্ডেল করতে একটু বেশি সতর্ক থাকতে হয়। আমরা যদি বেস-কেস টাকে শুরুতেই টেবিলে রেখে দিয়ে কাজ শুরু করি তাহলে জীবন কিছুটা সহজ হয়ে যায়। পুরো কোডটা হবে এরকম:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
int lcsIterative(string S, string W) { int n = S.size(); int m = W.size(); for (int i = 0;i < n;i++) mem[i][m] = 0; for (int j = 0;j < m;j++) mem[n][j] = 0; for (int i = n - 1; i >= 0; i--) { for (int j = m - 1; j >= 0; j--) { if (S[i] == W[j]) { mem[i][j] = mem[i + 1][j + 1] + 1; } else { mem[i][j] = max(mem[i + 1][j], mem[i][j + 1]); } } } return mem[0][0]; } |
শেষ করার আগে একটা মাথা খাটানোর জন্য প্রশ্ন। কিছু কিছু ক্ষেত্রে রিকার্সিভ ফাংশন ইটারেশনের থেকে দ্রুত কাজ করবে। ইটারেটিভ ডিপিকে সবসময় পুরা টেবিলটাই পূর্ণ করতে হবে কিন্তু রিকার্সিভ ডিপি পুরো টেবিল ফিলআপ না করেই অনেক ক্ষেত্রে রেজাল্ট বের করে আনতে পারবে। প্রশ্ন হলো কেন এরকম ঘটে এবং কি ধরনের ইনপুটের জন্য রিকার্সিভ ফাংশন ভালো কাজ করবে?
প্র্যাকটিস প্রবলেম: https://leetcode.com/problems/longest-common-subsequence/
রিলেটেড প্রবলেম – এডিট ডিসটেন্স
তোমাকে দু্টি স্ট্রিং $S$, $W$ দেয়া আছে। তুমি শুধুমাত্র $S$ স্ট্রিংটার উপর ৩টা অপারেশন করতে পারো, কোন একটা ক্যারেকটার বদলে দিতে পারো, কোন ক্যারেকটার মুছে ফেলতে পারো, যেকোন পজিশনে নতুন ক্যারেকটার ঢুকাতে পারো। তারমানে চেঞ্জ, ডিলিট, ইনসার্ট হলো তোমার ৩টা অপারেশন। এখন তোমার কাজ মিনিমাম অপারেশনে $S$ স্ট্রিংটা টাকে $W$ বানানো।
যেমন “blog” কে “bogs” বানাতে তুমি l মুছে ফেলে স্ট্রিং এর শেষে s ইনসার্ট করতে পারো।
হিন্টস: LCS এর মতোই দুইটা ইনডেক্স $i,j$ কে স্টেট রাখতে হবে। এখন তুমি চিন্তা করো স্ট্রিং $S$ থেকে কোন ক্যারেকটার মুছে ফেললে $i,j$ এর পরিবর্তন কিরকম হবে। ঠিক সেভাবে বাকি ২টি অপারেশনের জন্য কিভাবে $i,j$ পরিবর্তন হবে সেটা বের করো)
প্র্যাকটিস: https://leetcode.com/problems/edit-distance/
পরের পর্বে আমরা ক্লাসিকাল কয়েন চেঞ্জ প্রবলেম শিখবো। হ্যাপি কোডিং!
ফেসবুকে মন্তব্য
Powered by Facebook Comments