আগের পর্বগুলোয় যেসব প্রবলেম দেখেছি তার মধ‍্যে ফিবোনাচ্চি সবগুলোতেই আমাদেরকে কিছু না কিছু ম‍্যাক্সিমাইজ বা মিনিমাইজ করতে হয়। এগুলো ছাড়া ডাইনামিক প্রোগ্রামিং এর আরো কিছু ব‍্যবহার আছে, একটা হলো কোন একটা কাজ কত ভাবে করা যায় সেটা বের করা, আরেকটা হলো ডিসিশন প্রবলেম সলভ করা (অর্থাৎ কোন একটা কাজ করা যাবে কি যাবে না সেটা বের করা)।

শুরুতেই দেখবো সাবসেট সাম প্রবলেম। এই প্রবলেমটা অনেকটাই কয়েন চেঞ্জ প্রবলেমের মত, আশা করবো তুমি কয়েন চেঞ্জ নিয়ে লেখাটা পড়ে ফেলেছো, কারণ এবার আমি আগের মত এত বিস্তারিত বর্ণনা করবো না।

সাবসেট সাম

তোমাকে একটা ইন্টিজার অ‍্যারে $C$ দেয়া আছে এবং একটা ভ‍্যালু $W$ দেয়া আছে। তোমাকে বলতে হবে $C$ এর আইটেমগুলো দিয়ে কতভাবে $W$ বানানো যায়।

যেমন ধরা যাক $C =  \{5, 15, 3, 17, 12\}$ এবং $W = 20$। আমরা $3$ ভাবে $20$ বানাতে পারি -> $(5 + 15), (3 + 17), (5 + 3 + 12)$।

একটা $n$ সাইজের অ‍্যারের $2^{n-1}$ টা non-empty সাবসেট থাকে। আমরা ডাইনামিক প্রোগ্রামিং ব‍্যবহার করলে সবগুলো সাবসেট বের করতে হবে না।

কয়েন চেঞ্জ প্রবলেমের মতোই আমাদের সাবপ্রবলেম হলো $f(i, W)$, অর্থাৎ আমরা বের করতে চাই $i$ থেকে $n-1$ তম আইটেমগুলো নিয়ে কতভাবে $W$ বানানো যায়। আমাদের আবারো দুইটা চয়েজ:

• $i$ তম আইটেমটা ব‍্যবহার করলে পরের সাবপ্রবলেম হবে $f(i + 1, W – C[i])$
• $i$ তম আইটেমটা ব‍্যবহার না করলে পরের সাবপ্রবলেম হবে  $f(i + 1, W)$

আগেরবার আমরা দুটো সাবপ্রবলেমের মিনিমাম বা ম‍্যাক্সিমাম নিয়েছিলাম, এবার জাস্ট দুটোর রেজাল্ট যোগ করে দিতে। বেস কেস হবে $W = 0$, সেক্ষেত্রে আমরা টার্গেটে পৌছে গেছি, এসময় আমাদেরকে $1$ রিটার্ন করতে হবে।

কোডটা লিখে ফেলি:

কমপ্লেক্সিটিও কয়েন চেঞ্জের মতোই সুডোপলিনোমিয়াল $O(n*W)$ । ইটারেটিভ ভার্সন আমি আর দেখাচ্ছি, এখন তুমি নিজেই সেটা লিখতে পারবে।

সাবসেট সাম ডিসিশন প্রবলেম

এখন আমাদেরকে যদি বলতো $W$ কতভাবে বানানো যাবে সেটা বের করা দরকার নেই, $W$ বানানো যাবে নাকি যাবে না সেটা বের করে দাও। আগের কোডটা ব‍্যবহার করেই সেটা করা যাবে, উত্তর পজিটিভ মানে $W$ বানানো যায়। তবে সেটা আরো সহজে এবং কম মেমরি ব‍্যবহার করেই করা যায়।

এক্ষেত্রে আমরা ইন্টিজার রিটার্ন না করে বুলিয়ান true/false রিটার্ন করবো। যদি দুটি সাবপ্রবলেমের অন্তত একটা true রিটার্ন করে তাহলে রেজাল্ট হবে true।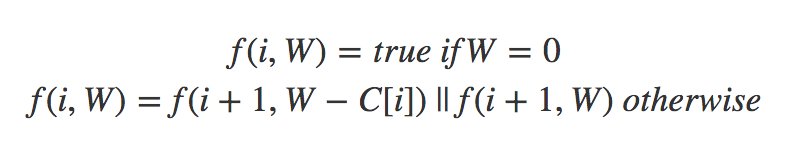এখানে || হলো লজিকাল OR অপারেটর।

কম্বিনেশন

তোমার কাছে $n$ টা আইটেম আছে, সেখান থেকে $r$ টা আইটেম তুলে নিতে হবে। কতভাবে করা যায়? এটা ক্লাসিক $^{n}C_{r}$ প্রবলেম যেটা হাইস্কুলেই সবাই পড়ে এসেছো। তখন আমরা এটার একটা ফর্মুলা মুখস্থ করে ফেলতাম: $\dfrac{n!}{(n-r)!r!}$।  এখন দেখি এটাকে রিকার্সিভলি কিভাবে লেখা যায়।

আমরা একটা ফাংশন ডিফাইন করি $f(n, r)$। এখন হাতে দুইটা চয়েজ:

• একটা আইটেম তুলে নেয়া, তাহলে বাকি থাকবে মোট $n-1$ টা আইটেম এবং তুলতে হবে আরো $r-1$ টা আইটেম, অর্থাৎ $f(n-1, r-1)$।
• একটা আইটেম ফেলে দেয়া, তাহলে বাকি থাকবে মোট $n-1$ টা আইটেম এবং তুলতে হবে আরো $r$ টা আইটেম, অর্থাৎ $f(n-1, r)$।

তাহলে আমরা উত্তর পেয়ে যাবো $f(n-1, r-1)$ আর  $f(n-1, r)$ যোগ করে দিলেই। বেসকেস সহ ফর্মুলা হবে:

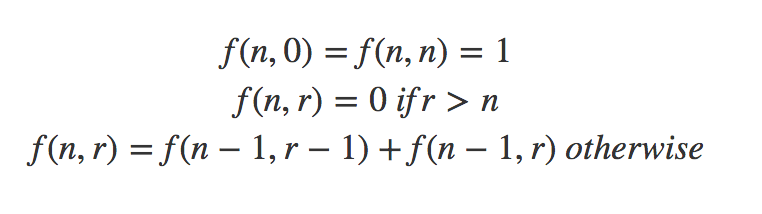এটার কোড আর দিব না, তুমি নিজেই লিখতে পারবে।

কতগুলো পথ?

তোমাকে একটা $n*m$ সাইজের ২ডি গ্রিড দেয়া আছে। তুমি বর্তমানে আছো গ্রিডের উপরের বাম কোনায় $(0,0)$, তোমাকে সেখান থেকে $(n-1, m-1)$ ঘরে যেতে হবে। বলতে হবে কতগুলো ভিন্ন ভিন্ন উপায়ে যাওয়া যায়। তুমি শুধু মাত্র ৩ ডিরেকশনে যেতে পারো, ডানে, নিচে বা কোনাকুনি। গ্রিডের কিছু কিছু সেল ব্লক করা আছে, সেগুলোতে যাওয়া যাবে না।

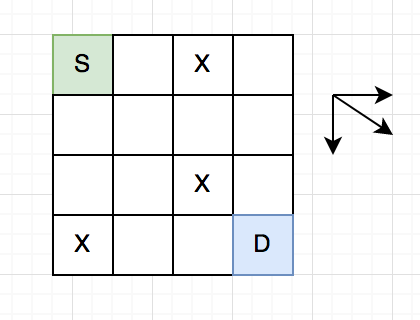৩ ডিরেকশনের শর্তটা দেয়া হয়েছে যাতে তুমি ঘুরেফিরে একই সেলে ফিরে আসতে না পারো, সেক্ষেত্রে সাইকেল তৈরি হয়ে যাবে,  DAG থাকবে না।

এই প্রবলেমটা খুবই সহজ। তোমার সাবপ্রবলেম হবে $f(i, j)$ এবং এখান থেকে তোমার ৩টা চয়েজ আছে। কি কি চয়েজ নিশ্চয়ই বুঝতে পারছো, সেগুলো যোগ করে দিলেই উত্তর বের হয়ে আসবে।

এখন আমরা যদি এটাকে ডিসিশন প্রবলেম হিসাবে চিন্তা করি, বের করতে চাই গন্তব‍্যে পৌছানো যায় কি যায় না তাহলে কি করবে? উত্তর গুলো যোগ না করে  লজিকাল OR  করে দিবে।

প্র‍্যাকটিস প্রবলেম:

https://leetcode.com/problems/unique-paths/
https://leetcode.com/problems/pascals-triangle/
https://leetcode.com/problems/partition-equal-subset-sum/