কনটেস্ট প্রোগ্রামিং এর একটা দারুণ ব্যাপার হলো কনটেস্টেন্টদের শুধু ভালো প্রোগ্রামিং জানলেই হয়না, সাথে ভালো গণিতও জানা দরকার হয়। বিশেষ করে কম্বিনেটরিক্স আর প্রোবাবিলিটিতে ভালো ধারণা থাকলে অনেক ধরণের প্রবলেম সলভ করে ফেলা যায়।
৪টি টুপি পাশাপাশি সাজানো আছে, টুপিগুলোকে যথাক্রমে ১,২,৩,৪ সংখ্যাগুলো দিয়ে চিহ্ন দেয়া হয়েছে। এখন টুপিগুলোকে এলোমেলো করে কতভাবে সাজানো যাবে? আমরা কয়েকভাবে সাজিয়ে চেষ্টা করি:
১,২,৩,৪
১,৩,২,৪
১,৪,২,৩
১,৩,৪,২
…….
……
৪,৩,২,১
মোট কতভাবে সাজানো যাবে? কলেজে করে আসা অংক থেকে তুমি সহজেই বলতে পারবে $factorial(৪)=২৪$ ভাবে সাজানো যায়। এটাকে আমরা একটু প্রোগ্রামারের দৃষ্টিভঙ্গী থেকে দেখি। ৪টা জায়গা বা স্লট আছে, প্রতিটি স্লটে ১টি করে টুপি বসানো যায়। এখন প্রথম স্লটে ১,২,৩ বা ৪ এর যেকোনো একটা বসালে:
১,_,_,_
প্রথম স্লটে টুপি কত ভাবে বসানো যায়? অবশ্যই ৪ ভাবে। এখন ২য় স্লটে কয়ভাবে বসানো যায়? একটা টুপি আমরা বসিয়ে ফেলেছি আগেরটায়, তাই ২য় স্লটে বসাতে পারবো ৪-১=৩ ভাবে। ঠিক এভাবে ৩য় স্লটে ২ভাবে এবং ২য় স্লটে ১ ভাবে। তাহলে মোট উপায় $৪ \times ৩ \times ২ \times ১=২৪$ টা। ৪টার জায়গায় $n$ টা টুপি থাকলে কি করতে? আমরা প্রোগ্রামার তাই বারবার কষ্ট করে হিসাব না করে ধুম করে একটা ফাংশন লিখে ফেলি। মনে করো ফাংশনটা হলো permutation(n)। $n=0$ হলে সাজানো যায় ১ ভাবে, তাহলে:
$permutation(0)=0$
$n>0$ হলে প্রথম স্লটে বসানো যায় $n$ ভাবে, এরপরে সমস্যাটা ছোটো হয়ে দাড়ায় “$n-1$ টা টুপি $n-1$ টা স্লটে কতভাবে বসানো যায়?” অর্থাৎ সমস্যাটা $permutation(n-1)$ হয়ে যায়। সাথে গুণ হবে $n$ কারণ কারেন্ট স্লটে $n$ ভাবে বসিয়েছি। তাহলে লিখতে পারি:
$permutation(n)=n \times permutation(n-1)$
আশা করি ব্যাপারটা পরিষ্কার। সহজ ব্যাপারটা নিয়ে এত কথা বললাম যাতে রিকার্শনটা পরিষ্কার হয় যেটা কাজে লাগবে ডিরেঞ্জমেন্ট গোণার জন্য।
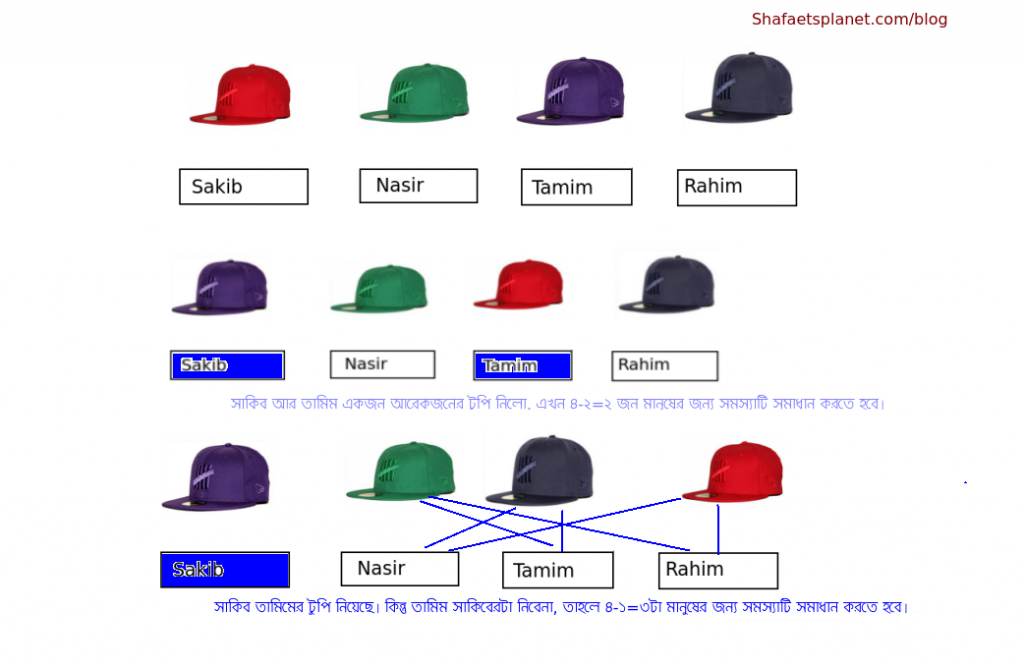
এখন ধরো ১,২,৩,৪ এই ৪টা টুপির মালিক হলো যথাক্রমে সাকিব, নাসির, তামিম, রহিম। তারা খুবই ভালো বন্ধু বলে ঠিক করলো একজন আরেকজনের টুপি পড়ে ক্রিকেট খেলতে যাবে। কেও তার নিজের টুপি পড়তে পারবেনা, তাহলে বন্ধুত্ব থাকবেনা! এখন কতভাবে তারা টুপি পড়তে পারবে?
গণিতের ভাষায় এর নাম ডিরেঞ্জমেন্ট, এমন কয়টি পারমুটেশন আছে যেখানে কেও তার নিজের জায়গায় নেই।
১,৩,২,৪ ডি-রেঞ্জমেন্ট নয় কারন সাকিব আর রহিম তাদের নিজ নিজ টুপিই পড়ে আছে(১ ও ৪ নম্বর) ! ২,১,৪,৩ একটি ডি-রেঞ্জমেন্ট, সবাই তার বন্ধুর টুপি পড়েছে।
আমরা একটা ফাংশন বানাবো $d(n)$ যেটা $n$ টা টুপি কতভাবে সাজানো যায় যাতে কেও তার নিজের টুপি না পায় সেটা বের করে দেয়।
প্রথম মানুষ সাকিবের কাছে ৪-১=৩টা চয়েস আছে, সে ১ নম্বর বাদে যেকোনো টুপি নিতে পারে। মনে করলাম সে তামিমের টুপি নিলো। এখন ২টা ঘটনা ঘটতে পারে:
১. পরের বার তামিম নিলো সাকিবের টুপি। এখন ৪-২=২ জন মানুষ বাকি, টুপিও বাকি ঠিক ৪-২=২ টা।
২. পরের বার তামিম সাকিব ছাড়া অন্য কারো টুপি নিলো। এখন মানুষ বাকি ৪-১=৩ জন। তামিম যেহেতু সাকিবের টুপি নিচ্ছেনা তাই ওটাকেই তার নিষিদ্ধ টুপি ধরতে হবে, আর বাকি সবার কাছে নিষিদ্ধ টুপি হলো তার নিজের টুপিটা। তাহলে এখন ৪-১=৩ জন মানুষের জন্য ৪-১=৩ টা করে চয়েস আছে। লক্ষ্য করো
দুই ক্ষেত্রেই মানুষ আর টুপির সংখ্যা সমান থাকছে। ৪ এর জায়গায় n ধরে ২টা কন্ডিশন মিলিয়ে সহজেই রিকার্সিভ রিলেশনটা লিখতে পারি:
$d(n)=(n-1)* (d(n-1)+d(n-2))$
বেস কেস: $d(1)=0,d(2)=1$
এই রিকার্সনটা কোড করার সময় মাথায় রাখতে হবে যে একই ফাংশন অনেকবার কল হচ্ছে,তাই ডিপি টেবিলে মানগুলো সেভ করে রাখতে হবে। তুমি ডাইনামিক প্রোগ্রামিং নিয়ে পড়ালেখা করতে পারো এ সম্পর্কে জানতে।
এবার আরেকটা মজার উপায়ে প্রবলেমটা সলভ করি। $^nC_r$ বা $\binom{n}{r}$ এর সাথে তোমরা পরিচিত, $n$ টা জিনিস থেকে $r$ টি জিনিস কতভাবে নেয়া যায় সেটাই প্রকাশ করে $\binom{n}{r}$ । $n$ টা টুপিকে মোট সাজানো যায় $n$! উপায়। এর মধ্যে যেসব পারমুটেশনে অন্তত একটি টুপি নিজের জায়গায় আছে তাদের বাদ দিলে ডিরেঞ্জমেন্ট পাওয়া যায়। $n$ টি টুপি থেকে ১ টি টুপি নেয়া যায় $\binom{n}{1}$ উপায়ে, ১টি টুপিকে নিজের জায়গায় রেখে বাকি $n-1$ টা টুপিকে সাজানো যায় $(n-1)!$ উপায়ে। তাহলে $n!- \binom{n}{1} \times (n-1)!$ বের করলেই ডিরেঞ্জমেন্ট বের হয়ে যাচ্ছেনা? কারণ আমরা মোট উপায় থেকে যেসব পারমুটেশনকে অন্তত ১ জন নিজের জায়গায় আছে তাদের বাদ দিচ্ছি। $\binom{n}{1}$ দিয়ে গুণ দিচ্ছি কারণ প্রতিবার ১জন কে ফিক্সড করে $n-1$ জনকে পারমুটেশন করতেসি।
কিন্তু এখানে একটা বড় সমস্যা আছে। ধরো তুমি তামিমের টুপিকে তামিমের কাছেই রেখে বাকি টুপিগুলো কয়ভাবে সাজানো যায় বের করলে। আবার নতুন করে সাকিবেরটা সাকিবের কাছে রেখে বাকিগুলো কয়ভাবে সাজানো যায় বের করলে। ভালোমত চিন্তা করে দেখ যেসব পারমুটেশনে সাকিবেরটা সাকিবের কাছে আছে আর তামিমেরটা তামিমের কাছে আছে সেগুলো কি ২বার গণনা করা হয়ে গেলো না? $\binom{n}{1} \times (n-1)!$ এ এই কারণে কিছু পারমুটেশন একাধিক বার ক্যালকুলেট করা হয়ে যাবে। সেগুলো আমরা কিভাবে বাদ দিবো? আমরা ১টা সংখ্যা ফিক্সড করে যখন গুনেছি তখন যেসব পারমুটেশনে ২টা সংখ্যা ফিক্সড সেগুলো একাধিক বার গুণে ফেলেছি, সেগুলো আমরা বাদ দিয়ে দেই। $\binom{n}{1} \times (n-1)!$ থেকে বাদ দিয়ে দিবো $\binom{n}{2} \times (n-2)!$ । একটু চিন্তা করলে বুঝতে পারবে এখানেও সমস্যা আছে, যেখানে ৩টা ফিক্সড সেগুলোকেও আমরা বাদ দিয়ে দিচ্ছি!! তাহলে সেটা আবার যোগ করে দাও। মাথা গুলিয়ে গেলে ভ্যান ডায়াগ্রামের কথা চিন্তা করো:
ভ্যান ডায়াগ্রামে ৩টা অংশের কমন এরিয়া বের করতে আমরা সবগুলো অংশ যোগ করি, তারপর যেসব অংশ দুটি বুত্তে আছে সেগুলো বাদ দেই, যেগুলো ৩টি বৃত্তে আছে সেগুলো আবার যোগ করে দেই, বৃত্ত আরো বেশি থাকলে এভাবে যোগ বিয়োগ চলতেই থাকে। দুটি সেট $A,B$ হলে $|A∪B|=|A|+|B|-|A∩B|$। ঠিক এই কাজটি করবো এখানে। আমাদের ফর্মূলা হবে:
$n!-\binom{n}{1} \times (n-1)!+ \binom{n}{2} \times (n-2)!-..…+ (-1)^k \times \binom{n}{k} \times (n-k)!+….+(-1)n$
আমরা একবার যোগ করছি, একবার বিয়োগ করছি, এভাবে অপ্রয়োজনীয় অংশ বাদ দিয়ে ফলাফল পেয়ে যাচ্ছি। এ জিনিসটারই রাশভারী নাম হলো ইনক্লুশন-এক্সক্লুশন প্রিন্সিপাল।
আজ এ পর্যন্তই। সলভ করার জন্য প্রবলেম:
www.topcoder.com/stat?c=problem_statement&pm=2013
http://uva.onlinejudge.org/external/112/11282.html
http://www.lightoj.com/volume_showproblem.php?problem=1095
ফেসবুকে মন্তব্য
Powered by Facebook Comments

আপনার ব্লগের একজন নিয়মিত পাঠক। ধন্যবাদ প্রোগ্রামিং নিয়ে লেখার জন্য।
আপনি কি uva 12022 সোলভ এর কোনো easy formula জানেন?
ভাইয়া, কয়েকটা প্রবলেমের আইডি বলেন সলভ করার জন্য।
http://uva.onlinejudge.org/external/112/11282.html
http://www.lightoj.com/volume_showproblem.php?problem=1095
@ হাসান
এই প্রব্লেমটাও derangement নিয়ে http://uva.onlinejudge.org/external/120/12024.html
@শাফায়েত ভাই, আপনার নতুন নতুন লেখার জন্য সবসময় অপেক্ষায় থাকি … আপনার এই ব্লগ আমার মত অসংখ্য সুবিধাবঞ্চিত আধা-প্রোগ্রামারদের অনেক-অনেক সাহায্য করছে , স্বপ্ন দেখাচ্ছে । আশা করি আপনি এখানে লেখা চালিয়ে যাবেন।
অন্তরের গভীর থেকে আপনার জন্য শ্রদ্ধা…
অনেকেই জিজ্ঞেস করে ব্লগ লিখে আমার লাভটা হয় কি,টাকাপয়সা পাই নাকি, আমি তাদের সবসময় বলি ব্লগ লিখে আমি কিছু মানুষের ভালোবাসা পাই,এর থেকে বড় কিছু হতে পারেনা। সত্যিই খুবই ভালো লাগলো তোমার মন্তব্যটি দেখে,আমি আন্তরিকভাবে চেষ্টা করবো আমার স্বল্প জ্ঞান দিয়েই আরো বেশি করে লেখালেখি করতে।
প্রাইম নাম্বারের সিভ থেকে শুরু করে আমার এই পর্যন্ত শিখা বেশীরভাগ algorithm ই আপনার ব্লগ থেকে । বলা যায় প্রোগ্রামিং এর খানিক অংশটাই এখান থেকে শিখা । অসংখ্য ধন্যবাদ আপনাকে ভাইয়া। আল্লাহ্ রাব্বুল আলামিন আপনার মঙ্গল করুন। আমীন।
শুনে ভালো লাগলো!
টাইপো, permutation(0)=0 এর বদলে permutation(0)=1 হবে।