[নোটিশ ২৩ এপ্রিল ২০২০: ডাইনামিক প্রোগ্রামিং এর নতুন সিরিজ শুরু করেছি। লেখাটি নতুন ভার্সন এখানে পাওয়া যাবে।
আমরা এবার আরো একটি ক্লাসিক ডাইনামিক প্রোগ্রামিং প্রবলেম দেখবো যেটার নাম ম্যাট্রিক্স চেইন মাল্টিপ্লিকেশন। এটা শেখা খুবই গুরুত্বপূর্ণ কারণ এটার ধারণা ব্যবহার করে অনেক ধরণের সমস্যা সমাধান করে ফেলা যায়। এই লেখাটা পড়ার আগে তোমার ডাইনামিক প্রোগ্রামিং এর ধারণা থাকতে হবে। এছাড়া ম্যাট্রিক্স নিয়েও ধারণা থাকতে হবে।
আমি নিশ্চিত তোমরা সবাই ম্যাট্রিক্স গুণের শর্তগুলো জানো, তাও আমি মনে করিয়ে দিতে চাই। ধরি আমাদের দুটি ম্যাট্রিক্স আছে $A_1, A_2$ এবং তাদের ডিমেনশন $m * n$ আর $p * q$। তাহলে কয়েকটি প্রোপার্টি আমাদের জন্য গুরুত্বপূর্ণ:
- ম্যাট্রিক্স দুটি গুণ করা যাবে তখনই যদি $n=p$ হয়। তারমানে প্রথম ম্যাট্রিক্সের কলাম সংখ্যা, দ্বিতীয় ম্যাট্রিক্সের রো এর সংখ্যার সমান হতে হবে।
- যদি আগের শর্ত পূরণ হয় তাহলে গুণ করার পর আমরা $A_3$ ম্যাট্রিক্স পাবো যার ডিমেনশন $m * q$।
- ম্যাট্রিক্স গুণ করার সময় আমাদের কিছু সংখ্যাকে গুণ করে যোগ করতে হয় যেগুলোকে আমরা স্কেলার গুণ বলতে পারি। আমাদের মোট স্কেলার গুণ করা লাগবে মোট $m * n * q$ বা $m * p * q$ বার।
তুমি দুটি ম্যাট্রিক্স খাতায় লিখে গুণ করে যাচাই করে দেখতে পারো ব্যাপারগুলো। আরেকটা জিনিস মনে রাখবে যে $A_1*A_2$ আর $A_2*A_1$ এক না, অর্থাৎ অর্ডার ভঙ্গ করে আমরা ম্যাট্রিক্স গুণ করতে পারবো না।
এই লেখায় যখন সংখ্যাগুণের কথা বা শুধু “গুণ” এর কথা বলা হয়েছে তখন ম্যাট্রিক্সগুণ করার সময় ভিতরে যে সংখ্যাগুলো গুণ করতে হয় সেটা বুঝানো হয়েছে।
[নোটিশ ২৩ এপ্রিল ২০২০: ডাইনামিক প্রোগ্রামিং এর নতুন সিরিজ শুরু করেছি। লেখাটি নতুন ভার্সন এখানে পাওয়া যাবে।
তাহলে যদি আমাদের ৩টা ম্যাট্রিক্স থাকে A1,A2,A3 যাদের ডিমেনশন $m * n$,$n * p$, $p * q$ তাহলে $A_4=A_1*A_2*A_3$ ম্যাট্রিক্সের ডিমেনশন হবে $m * q$। উপরের ২য় প্রোপার্টি থেকেই এই ব্যাপারটা বোঝা যাচ্ছে। এখন A1*A2*A3 এই ম্যাট্রিক্স গুণটা আমরা দুইভাবে করতে পারি, ব্রাকেট দিয়ে সেগুলো এভাবে দেখানো যায়: $(A_1*A_2)*A_3, A_1*(A_2*A_3)$। অর্থাৎ আমরা $A_1*A_2$ এর সাথে $A_3$ কে গুণ করতে পারি, অথবা $A_1$ কে $A_2*A_3$ এর সাথে গুণ করতে পারি। তবে অর্ডার অবশ্যই ঠিক রাখতে হবে, $(A_1*A_3)*A_2$ এটা ভ্যালিড নাও হতে পারে।
বুঝতে পারছো অর্ডার ঠিক রেখে অনেকভাবে ব্রাকেট বসিয়ে গুণ করা যায়। কিন্তু কিভাবে ব্রাকেট বসাচ্ছি সেটা খুবই গুরুত্বপূর্ণ। ধরা যাক $A_1, A_2, A_3$ এর ডিমেনশন ১০×১০০, ১০০×৫, ৫×৫০।
তাহলে
$(A_1*A_2)*A_3$ এই ব্রাকেটিং এ মোট সংখ্যা গুণ করতে হবে (১০×১০০×৫) + (১০×৫×৫০) = ৭৫০০ বার
$A_1*(A_2*A_3)$ এই ব্রাকেটিং এ মোট সংখ্যা গুণ করতে হবে (১০০×৫×৫০) + (১০×১০০×৫০) = ৭৫,০০০ বার
(এখানে মাল্টিপ্লিকেশন বলতে ম্যাট্রিক্স গুণ করার সময় কয়বার ভিতরে স্কেলার গুণ করা হচ্ছে সেটা বুঝানো হয়েছে, ৩নম্বর শর্ত দেখো)
২য় উপায়ে ১০গুণ বেড়ে গিয়েছে ক্যালকুলেশনের পরিমাণ! ম্যাট্রিক্স চেইন মাল্টিপ্লিকেশন পদ্ধতি ব্যাবহার করে আমরা এমন একটা “ব্রাকেটিং” বের করবো যাতে সংখ্যা গুণের পরিমাণ সবথেকে কম হয়। তোমাকে $A_1,A_2……..A_n$ এরকম অনেকগুলো ম্যাট্রিক্সের শুধুমাত্র ডিমেনশন দেয়া থাকবে, বলতে হবে মিনিমাম কয়টা সংখ্যা গুণ করে $A_1*A_2*………..A_n$ বের করা যায়। আমরা ধরে নিচ্ছি ডিমেনশনগুলো ভ্যালিড, অর্থাৎ প্রথম শর্ত পূরণ করে।
আমরা ডিভাইড এন্ড কনকোয়ার পদ্ধতিতে এটা সলভ করবো। ডাইনামিক প্রোগ্রামিং দরকার হবে কারণ একই সাবপ্রবলেম বারবার আসবে। ধরি $n$ এর মান ৫, তাহলে $A_1,A_2,A_3,A_4,A_5$ এই ৫টা ম্যাট্রিক্স আছে, তুমি $A_1*A_2*A_3*A_4*A_5$ বের করতে কয়টা সংখ্যা গুণ লাগে সেটা বের করতে চাও। এখন দেখো আমরা বিভিন্ন ভাবে ম্যাট্রিক্সগুলোকে দুইভাগে ভাগ করে ফেলতে পারি, যেমন একটা উপায় হলো এরকম:
$(A_1*A_2)*(A_3*A_4*A_5)$
তারমানে আমরা কোন একটা ব্রাকেটিং এ $A_{left}=A_1*A_2$ বের করবো এবং কোন একটা ব্রাকেটিং এ $A_{right}=A_3*A_4*A_5$ বের করবো। আমরা জানিনা কিভাবে সেগুলো বের করবো, তবে কেও যদি আমাদের বলে দেয় $A_{left}$ আর $A_{right}$ বের করতে কয়টা সংখ্যা গুণ করা লাগে তাহলে আমরা বলে দিতে পারবো মোট কয়টা সংখ্যা গুণ করা লাগে। মোট সংখ্যা গুণের সংখ্যা হবে:
মোট গুণের সংখ্যা = $A_{left}$ নির্ণয় করতে গুণের সংখ্যা + $A_{right}$ নির্ণয় করতে গুণের সংখ্যা + $A_{left}*A_{right}$ নির্ণয় করতে গুণের সংখ্যা
বা ৩য় শর্ত থেকে শেষ টার্মটাকে লিখতে পারি: $A_{left}$ এর রো সংখ্যা× $A_{left}$ এর কলাম সংখ্যা×$A_{right}$ এর কলাম সংখ্যা
মোট গুণের সংখ্যা = $A_{left}$ নির্ণয় করতে গুণের সংখ্যা + $A_{right}$ নির্ণয় করতে গুণের সংখ্যা + $A_{left}$ এর রো সংখ্যা×$A_{left}$ এর কলাম সংখ্যা×$A_{right}$ এর কলাম সংখ্যা
তারমানে কেও যদি ম্যাজিকালি $A_{left}$ এর $A_{right}$ বের করে দেয় তাহলেই আমরা মোট সংখ্যা বের করতে পারবো।
কিন্তু আমরাতো আরো অনেকভাবে ভাগ করতে পারতাম, যেমন:
$(A_1)*(A_2*A_3*A_4*A_5)$
$(A_1*A_2*A_3)*(A_4*A_5)$
$(A_1*A_2*A_3*A_4)*(A_5)$
আমরা প্রতিটা উপায়েই ভাগ করবো এবং ভাগ করার পর ম্যাজিকালি $A_{left}$ এবং $A_{right}$ নির্ণয় করতে কয়টা সংখ্যা গুণ করা লাগে সেটা বের করে ফেলে মোট সংখ্যা বের করে ফেলবো। যেভাবে ভাগ করলে মোট সংখ্যাটা মিনিমাম হয় সেটাই আমার উত্তর!
তুমি যদি রিকার্শন ভালো করে বুঝে থাকো তাহলে এতক্ষণে বুঝে গিয়েছো ম্যাজিকালি কিভাবে কাজটা করা হবে। বাম আর ডান পাশের ভাগগুলোকে আমরা রিকার্সিভলি সলভ করে ফেলবো একইভাবে, অর্থাৎ সেগুলোকে আবার অনেকভাবে ভাগ করে অপটিমাল উত্তরটা বের করে আনবো! তাহলে আমাদের অ্যালগোরিদম দাড়ালো খুব সহজ:
যত উপায়ে সম্ভব ভাগ করো
রিকার্সিভলি ছোট ভাগগুলোর জন্য সমাধান করো
বাম আর ডান পাশ মার্জ করে মোট গুণের সংখ্যা বের করো
সবগুলো উপায়ের মধ্যে সবথেকে ভালোটা নাও
তাহলে চিন্তা করো আমাদের রিকার্শনের প্যারামিটার বা স্টেট কি হবে? কি কি তথ্য আমাকে দিলে আমি প্রবলেমটা সলভ করতে পারি? আমার শুধু জানা দরকার ইনপুট ম্যাট্রিক্সগুলোর কোন অংশ নিয়ে আমি এখন কাজ করছি। তারমানে আমরা শুরুর পয়েন্ট আর শেষের পয়েন্ট স্টেট হিসাবে রাখবো।
int f(int beg, int end)
এরকম হবে ফাংশনের প্যারামিটার বা স্টেট। $f$ ফাংশনটা $beg$ থেকে $end$ পর্যন্ত ম্যাট্রিক্সগুলোকে সবথেকে অপটিমালি গুণ করলে মোট কয়টা সংখ্যা গুণ করা লাগে সেটা বলে দিবে! রিকার্শন থামবে কখন? অর্থাৎ বেস কেসটা কি? যখন দেখবো একটা বা তারথেকে কম ম্যাট্রিক্স আছে $(b>=e)$ তখন আমরা জানি একটা গুণও করা লাগবেনা, শূন্য রিটার্ণ করে দিবো।
তাহলে আমরা এখন একটা কোড লিখে ফেলি। সবথেকে ভালো হয় যদি তারআগে তুমি নিজেই একবার চেষ্টা করো, সাহায্য না নিয়ে সলভ করতে পারলে যে আনন্দ পাওয়া যায় তার তুলনা নেই! আর না পারলেও মন খারাপের কিছু নেই। ইনপুট হিসাবে তুমি প্রতিটি ম্যাট্রিক্সের রো এবং কলাম সংখ্যা নিবে। আউটপুট হবে অপারেশন সংখ্যা।
স্টেট পাওয়ার পরে আমাদের কাজ হবে এক স্টেট থেকে অন্য স্টেটে কিভাবে যাবো, অর্থাৎ রিকারেন্স রিলেশনটা বের করা। এই প্রবলেমে আমরা একটা করে মিডপয়েন্ট সিলেক্ট করে বাম আর ডানের পাশের জন্য প্রবলেমটা রিকার্সিভলি সলভ করবো এবং তাদের মার্জ করবো। রিকারেন্সটা তাহলে হবে এরকম: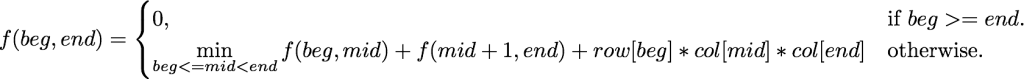
এবার আমরা এটাকে কোডে রূপান্তর করে ফেলি:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
#define MAX 100 int row[MAX], col[MAX]; int dp[MAX][MAX]; bool visited[MAX][MAX]; int f(int beg,int end) { if(beg>=end)return 0; if(visited[beg][end])return dp[beg][end]; int ans=1<<30; //২^৩০ কে ইনফিনিটি ধরছি for(int mid=beg; mid<end;mid++) //দুইভাগে ভাগ করছি { int opr_left = f(beg, mid); //opr = multiplication operation int opr_right = f(mid+1, end); int opr_to_multiply_left_and_right = row[beg]*col[mid]*col[end]; int total = opr_left + opr_right + opr_to_multiply_left_and_right; ans = min(ans, total); } visited[beg][end] = 1; dp[beg][end] = ans; return dp[beg][end]; } int main() { int n; cin>>n; rep(i,n)cin>>row[i]>>col[i]; cout<<f(0,n-1)<<endl; } |
খুবই সহজ একটা কোড, দুইভাগে ভাগ করছি আর ছোট ভাগটা সলভ করছি। একই অংশের জন্য বারবার সলভ করতে চাইনা তাই ডিপি অ্যারেতে সেভ করে রাখছি, যদি দেখি কোন একটা স্টেট আগে ভিজিট করা হয়েছে তখন পুরোনো রেজাল্ট রিটার্ণ করে দিচ্ছি!
কমপ্লেক্সিটি:
beg আর end এর মান হতে পারে $1$ থেকে n পর্যন্ত। তাহলে ভিন্ন স্টেট আছে প্রায় $n^2$ টা। প্রতিটা স্টেটে আবার $n$ পর্যন্ত লুপ চলতে পারে। তাহলে টাইম কমপ্লেক্সিটি O(n^3)। মেমরি লাগবে $O(n^2)$।
রিলেটেড প্রবলেম:
সরাসরি ম্যাট্রিক্স চেইন মাল্টিপ্লিকেশনের প্রবলেম হয়তো তুমি কনটেস্টে পাবেনা তবে এভাবে দুই প্রান্তকে স্টেট ধরে বিভিন্নভাবে ভাগ করার আইডিয়া দিয়ে অনেক প্রবলেম সলভ করতে পারবে যে কারণে এটা শেখা এত গুরুত্বপূর্ণ
১. http://www.spoj.com/problems/MIXTURES/
[নোটিশ ২৩ এপ্রিল ২০২০: ডাইনামিক প্রোগ্রামিং এর নতুন সিরিজ শুরু করেছি। লেখাটি নতুন ভার্সন এখানে পাওয়া যাবে।
ফেসবুকে মন্তব্য
Powered by Facebook Comments

এই লিখাটার জন্যে অনেক দিন ধরে ওয়েট করছিলাম । শেষমেশ পেয়েও গেলাম ।
ধন্যবাদ 🙂
Thank you vaia…Article ta khub Valo laglo.