বেলম্যান ফোর্ড গ্রাফে শর্টেস্ট পাথ বের করার একটা অ্যালগোরিদম। এই অ্যালগোরিদম একটা নোডকে সোর্স ধরে সেখান থেকে সব নোডের সংক্ষিপ্ততম বা শর্টেস্ট পথ বের করতে পারে। আমরা একদম শুরুতে এই কাজ করার জন্য ব্রেডথ ফার্স্ট সার্চ শিখেছি। কিন্তু বিএফএস(BFS) যেহেতু ওয়েটেড গ্রাফে কাজ করে না তাই এরপর আমরা শিখেছি ডায়াক্সট্রা অ্যালগোরিদম। এখন বেলম্যান ফোর্ড শিখব কারন আগের কোনো অ্যালগোরিদমই নেগেটিভ ওয়েট এর এজ আছে এমন গ্রাফে কাজ করে না।
আমরা ডায়াক্সট্রা শেখার সময় রিল্যাক্সেশন নামের একটা ব্যাপার শিখেছিলাম। তোমার যদি মনে না থাকে বা ডায়াক্সট্রা না শিখে থাকো তাহলে আমরা প্রথমে একটু ঝালাই করে নেই আরেকবার। মনে থাকলে পরের অংশটা বাদ দিয়ে সরাসরি এখানে যেতে পার।
এজ রিল্যাক্সেশন:
ধর একটা গ্রাফে সোর্স থেকে প্রতিটা নোডের ডিসটেন্স/কস্ট রাখা হয়েছে $d[]$ অ্যারেতে। যেমন $d[3]$ মানে হলো সোর্স থেকে বিভিন্ন এজ পার হয়ে ৩ নম্বর নোড এ আসতে মোট $d[3]$ ডিসটেন্স পার করতে হয়েছে। যদি ডিসটেন্স জানা না থাকে তাহলে ইনফিনিটি অর্থাৎ অনেক বড় একটা মান রেখে দিবো। আর $cost[u][v]$ তে রাখা আছে $u-v$ এজ এর cost।
ধর তুমি বিভিন্ন জায়গা ঘুরে ফার্মগেট থেকে টিএসসি তে গেলে ১০ মিনিটে, আবার ফার্মগেট থেকে কার্জন হলে গেলে ২৫ মিনিটে। তাহলে ফার্মগেটকে সোর্স ধরে আমরা বলতে পারি:
d[টিএসসি] = ১০, d[কার্জন হল] = ২৫
এখন তুমি দেখলে টিএসসি থেকে ৭ মিনিটে কার্জনে চলে যাওয়া যায়,
cost[টিএসসি][কার্জন হল] = ৭
তাহলে তুমি ২৫ মিনিটের জায়গায় মাত্র ১০ + ৭ = ১৭ মিনিটে কার্জ নহলে যেতে পারবে। যেহেতু তুমি দেখেছো:
d[টিএসসি]+cost[টিএসসি][কার্জন] < d[কার্জন হল]
তাই তুমি এই নতুন রাস্তা দিয়ে কার্জন হলে গিয়ে d[কার্জন হল] = d[টিএসসি] + cost[টিএসসি][কার্জন হল] বানিয়ে দিতেই পারো!!
উপরের ছবিটা সেটাই বলছে। আমরা $u$ থেকে $v$ তে যাবো যদি d[u]+cost[u][v] < d[v] হয়। আর $d[v]$ কে আপডেট করে $d[v] = d[u] + cost[u][v]$ বানিয়ে দিবো। ভবিষ্যতে যদি কার্জনহলে অন্য রাস্তা দিয়ে আরো কম সময়ে যেতে পারি তখন সেই রাস্তা এভাবে কম্পেয়ার করে আপডেট করি দিবো। ব্যাপারটা অনেকটা এরকম:
|
1 2 |
if(d[u]+cost[u][v] < d[v]) d[v] = d[u] + cost[u][v]; |
এটাই হলো এজ রিল্যাক্সেশন। এখন আমরা বেলম্যান ফোর্ড শেখার জন্য তৈরি।
বেলম্যান ফোর্ড
নিচের গ্রাফে আমরা ১ থেকে শুরু করে প্রতিটা নোডে যাবার শর্টেস্ট পাথ বের করতে চাই:

শুরুতে $d[1]=0$ কারণ ১ হলো সোর্স। বাকিসবগুলোতে ইনফিনিটি রেখেছি কারণ আমরা এখনও জানিনা শর্টেস্ট পাথের কস্ট কত।
তুমি এজ রিল্যাক্স কিভাবে করতে হয় এরই মধ্যে শিখে গেছ। এখন কাজ হলো সবগুলো এজকে একবার করে রিল্যাক্স করা, যেকোন অর্ডারে। একবার ‘গ্রাফ রিল্যাক্স’ করার মানে হল গ্রাফটার সবগুলো এজকে একবার করে রিল্যাক্স করা। আমি নিচের অর্ডারে রিল্যাক্স করতে চাই,
| Serial | 1 | 2 | 3 | 4 | 5 | 6 |
| Edge | 4 -> 5 | 3 -> 4 | 1 -> 3 | 1 -> 4 | 4 -> 6 | 2 -> 3 |
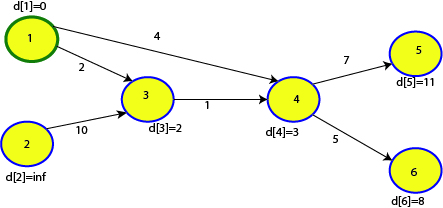
তুমি চাইলে অন্য যেকোনো অর্ডারেও এজগুলো নিতে পারতে। এখন চিন্তা কর এজগুলোকে একবার রিল্যাক্স করলে আমরা d[] অ্যারেতে কি পাব? সোর্স থেকে শুরু করে সর্বোচ্চ ১টা এজ ব্যবহার করে অন্যান্য নোডে যাবার শর্টেস্ট পাথের কস্ট আমরা পেয়ে যাব। উপরের ছবিতে রিল্যাক্স করার পর d[] এর মানগুলো আপডেট করে দাও। করার পর ছবিটা নিচের মত হবার কথা:
এজ রিল্যাক্স করার সময় কিছু নোড এর কস্ট আপডেট করতে পারি নি কারণ d[u]+cost[u][v] < d[v] শর্তটা পূরণ করে নি। বাকি এজগুলো আপডেট করার পর $d[]$ অ্যারের এর মান উপরের ছবির মত পেয়েছি। ১ নম্বর নোড থেকে শুরু করে সর্বোচ্চ একটি এজ ব্যবহার করে সব নোডে যাবার শর্টেস্ট পাথ এখন আমরা জানি!
এখন সর্বোচ্চ ২টা এজ ব্যবহার করে সব নোডে যাবার শর্টেস্ট পাথের cost বের করতে আরেকবার রিল্যাক্স করে ফেলি! আবারো যেকোন অর্ডারে করা যাবে, তবে প্রথমে যে অর্ডারে করেছি সেভাবেই প্রতিবার করা কোড লেখার সময় সুবিধাজনক।
একটা ব্যাপার লক্ষ্য কর, ১ থেকে ৬ তে যাবার শর্টেস্ট পথে ৩ টা এজ আছে (১->৩, ৩->৪, ৪->৬) এবং পথের দৈর্ঘ্য ২+১+৫=৮। মাত্র ২বার রিল্যাক্স করলেও আমরা এখনই d[6] তে ৮ পেয়ে গেছি, অথচ আমাদের এখন সর্বোচ্চ ২টা এজ ব্যবহার করে শর্টেস্ট পাথের cost পাবার কথা। এটা নির্ভর করে তুমি কোন অর্ডারে এজ রিল্যাক্স করেছ তার উপর। সে কারণে ৫ এ যাবার শর্টেস্ট পাথ ১০ হলেও d[5] এ এখনো ১০ পাইনি। X বার ‘গ্রাফ রিল্যাক্স’ করলে সর্বোচ্চ X টা এজ ব্যবহার করে সোর্স প্রতিটা নোডে যাবার শর্টেস্ট পাথ তুমি নিশ্চিত ভাবে পাবে। X এর থেকে বেশি এজের ব্যাবহার করে প্রতিটা নোডে যাবার শর্টেস্ট পাথ তুমি X বার গ্রাফ রিল্যাক্সের পর পেতেও পার, নাও পেতে পার, সেটা এজ এর অর্ডারের উপর নির্ভর করে।
এখন ৩য় বারের মত রিল্যাক্স করি:
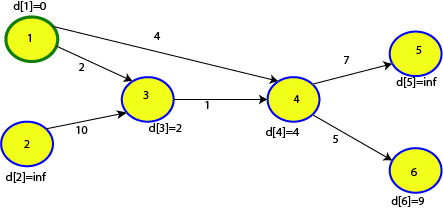
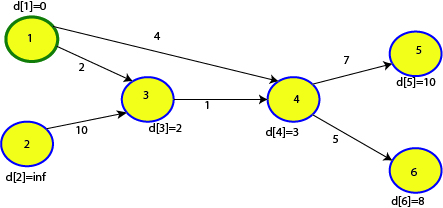 এবার শুধু মাত্র ৫ নম্বর নোড আপডেট হবে।
এবার শুধু মাত্র ৫ নম্বর নোড আপডেট হবে।
এরপরে আমরা আর যতই আপডেট করি, $d[]$ অ্যারেতে কোনো পরিবর্তন হবে না, আমরা ১ থেকে প্রতিটা নোডে যাবার শর্টেস্ট পাথ পেয়ে গিয়েছি।
এখন স্বাভাবিকভাবেই প্রশ্ন আসবে যে রিল্যাক্স কয়বার করতে হবে? গ্রাফে যদি নোড n টা থাকে তাহলে এক নোড থেকে অন্য নোডে যেতে সর্বোচ্চ $n-1$ টা এজ ব্যবহার করতে হবে। তারমানে কোনো নোড সর্বোচ্চ $n-1$ বার আপডেট হতে পারে। তাই রিল্যাক্স করার লুপটাও চালাতে হবে $n-1$ বার। তবে আমরা যেরকম উপরের গ্রাফে দেখেছি ৩বারের পরেই আর কোন নোড আপডেট করা যাচ্ছে না, সেরকম হলে আর নতুন করে রিল্যাক্স করার দরকার নাই।
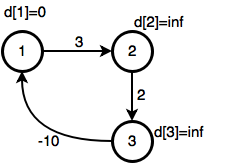
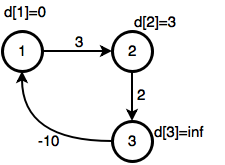
এখন নিচের মাত্র ৩নোডের গ্রাফটায় বেলম্যান ফোর্ড অ্যালগোরিদম চালাও, অর্থাৎ যতক্ষণ কোন নোড আপডেট করা যায় ততক্ষণ পুরো গ্রাফটা রিল্যাক্স কর:
| Serial | 1 | 2 | 3 |
| Edge | 2 -> 3 | 1 -> 2 | 3 -> 1 |
প্রথমবার রিল্যাক্স করার পর পাব:
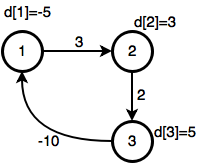
২য়বার করার পর:
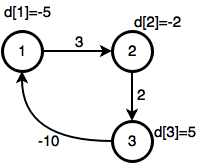
৩ নোডের গ্রাফে সোর্স থেকে কোনো নোডে শর্টেস্ট যেতে ২টার বেশি এজ লাগবে না, ৩য় বার রিল্যাক্স করার চেষ্টা করলে কোনো নোড আপডেট হবার কথা না। কিন্তু এই গ্রাফে আপডেট হচ্ছে:
এটা হচ্ছে কারণ $1->2->3->1$ সাইকেলটার মোট ওয়েট নেগেটিভ ($3 + 2 – 10 = -5$)। তাই তুমি যতবার এই সাইকেলে ঘুরবে শর্টেস্ট পাথ তত ছোট হতে থাকবে। তাই নেগেটিভ সাইকেল থাকলে এবং সোর্স থেকে সেই নেগেটিভ সাইকেলে যাবার পথ থাকলে সোর্সের শর্টেস্ট পাথ আনডিফাইনড বা অসংজ্ঞায়িত। যদি $n-1$ বার গ্রাফ রিল্যাক্স করার পর দেখি যে $n$ তম বারও কোনো নোডের cost আপডেট করা যায় তখন বুঝতে হবে আমরা নেগেটিভ সাইকেলে গিয়ে পরেছি, শর্টেস্ট পাথ বের করা সম্ভব না।
আমাদের সুডোকোড তাহলে হবে এরকম:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Input: A non-empty connected weighted graph G with vertices G.V and edges G.E procedure Bellman Ford(G,source): 1 Let distance[] ← infinity 2 Let N ← number of nodes 3 distance[source] = 0 4 for step from 1 to N-1 5 for all edges from (u,v) in G.E 6 if distance[u] + cost[u][v] < distance[v] 7 distance[v] = distance[u] + cost[u][v] 8 end if 9 end for 10 end for 11 for all edges from (u,v) in G.E 12 if distance[u] + cost[u][v] < distance[v] 13 return “Negative cycle detected 14 end if 15 end for 16 return distance |
পাথ প্রিন্ট করা:
বিএফএস বা ডায়াক্সট্রাতে যেভাবে পাথ প্রিন্ট করে ঠিক সেভাবে এখানেও পাথ প্রিন্ট করা যাবে। $previous[]$ নামের একটা অ্যারে নাও। $previous[v] = u$ মানে হলো $v$ তম নোডে তুমি $u$ থেকে এসেছ। শুরুতে অ্যারেতে ইনফিনিটি থাকবে। $u->v$ এজটা রিল্যাক্স করার সময় $previous[v] = u$ করে দাও। এখন তুমি $previous$ অ্যারে দেখে সোর্স থেকে যেকোন নোডের পাথ বের করে ফেলতে পারবে।
কমপ্লেক্সিটি:
সর্বোচ্চ $n-1$ বার প্রতিটা এজকে রিল্যাক্স করতে হবে, টাইম কমপ্লেক্সিটি $O(n*e)$।
চিন্তা করার জন্য কিছু প্রবলেম:
- তোমাকে একটা গ্রাফ দিয়ে বলা হল শর্টেস্ট পাথে সর্বোচ্চ $x$ টা এজ থাকতে পারে। এবার কিভাবে শর্টেস্ট পাথ বের করবে? (UVA 11280)
- একটি গ্রাফে কোন কোন নোড নেগেটিভ সাইকেলের অংশ কিভাবে বের করবে? (হিন্টস: স্ট্রংলি কানেক্টেড কম্পোনেন্ট + বেলম্যান ফোর্ড)
রিলেটেড কিছু প্রবলেম:
UVA 558(সহজ)
LOJ 1108
UVA 10449
হ্যাপি কোডিং!
ফেসবুকে মন্তব্য
Powered by Facebook Comments


ভাইয়া আপনাকে অনেক ধন্যবাদ 🙂 ।গ্রাফ থিওরির পাশাপাশি DP আর ডাটা স্ট্রাকচার নিয়ে আরও নতুন কোন পোস্ট দিলে খুবই খুশি হতাম 🙂
এজ রিলাক্স করাটা উপরে বুঝলাম, কিন্তু নিচে, মানে টেবিল এ বুঝি নাই।
” একবার ‘গ্রাফ রিল্যাক্স’ করার মানে হল গ্রাফটার সবগুলো এজকে একবার করে রিল্যাক্স করা।”
Shafaet vi, It’s very pleasing to learn any thing in Bangla .Thank u for ur contribution and hope it continues for us.:-)
if distance[u] + cost[u][v] < distance[v]
distance[u]=distance[v]+1
I think it's wrong :\ it should be
distance[v] = distance[u] + cost[u][v];
ঠিক করে দিলাম, ধন্যবাদ।