তোমাকে একটা লিংকড লিস্ট দেয়া আছে, বলতে হবে লিংকড লিস্টে কোনো সাইকেল আছে নাকি। এটা খুবই কমন একটা ইন্টারভিউ প্রশ্ন, আমরা ফ্লয়েডের সাইকেল ফাইন্ডিং অ্যালগোরিদম দিয়ে এই সমস্যাটা সমাধান করা শিখবো।
(If you want to read the same article in english, go to my english blog)
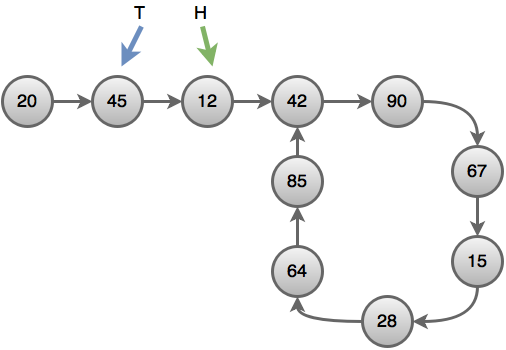
 ছবির লিংকড লিস্টে দেখা যাচ্ছে ৭ দৈর্ঘ্যের একটা সাইকেল আছে।
ছবির লিংকড লিস্টে দেখা যাচ্ছে ৭ দৈর্ঘ্যের একটা সাইকেল আছে।
সাইকেল ডিটেক্ট করার সবথেকে সহজ উপায় হলো ডিকশনারি বা হ্যাশম্যাপ ব্যবহার করা। প্রথম নোড থেকে এক এক ঘর আগাতে হবে এবং প্রতিটা নোডকে ডিকশনারিতে সেভ করে রাখতে হবে। যদি কোনো নোডে গিয়ে দেখা যায় নোডটা আগে থেকেই ডিকশনারিতে আছে তাহলে বুঝতে হবে লিংকড লিস্টটা সাইক্লিক। এই অ্যালগোরিদমের টাইম কমপ্লেক্সিটি আর মেমরি কমপ্লেক্সিটি দুইটাই $O(n)$।
মেমরি কমপ্লেক্সিটি $O(1)$ এ নামিয়ে আনা সম্ভব ফ্লয়েডের অ্যালগোরিদম ব্যবহার করে। এই অ্যালগোরিদমটাকে অনেকে “খরগোশ-কচ্ছপ অ্যালগোরিদম” বলে।
মনে করো আমাদের দুটি পয়েন্টার আছে, একটার নাম কচ্ছপ পয়েন্টার যেটাকে আমরা $T$ (Tortoise) দিয়ে চিহ্নিত করবো, আরেকটার নাম খরগোশ পয়েন্টার যেটাকে আমরা $H$ (Hare) দিয়ে চিহ্নিত করবো। শুরুতে দুইটা পয়েন্টারই লিংকড লিস্টের রুট নোড এ থাকবে।
প্রতি সেকেন্ডে খরগোশ আগাবে দুইঘর কিন্তু কচ্ছপ আগাবে মাত্র এক ঘর। তাহলে ১ সেকেন্ড পরে পয়েন্টার দুটোর পজিশন হবে এরকম:
আরো ১ সেকেন্ড পরে $T$ থাকবে $12$ নম্বর নোডে, $H$ থাকবে $90$ নম্বর নোডে। এভাবে কয়েক ধাপ হাতে-কলমে সিমুলেট করলে দেখবে দুইটি পয়েন্টারই $28$ নম্বর নোডে মিলিত হয়েছে।
দুটি পয়েন্টার একই নোডে মিলিত হওয়ার মানে হলো লিংকড-লিস্টে অবশ্যই সাইকেল আছে। সাইকেল না থাকলে $H$ পয়েন্টারটি সামনে আগাতে আগাতে লিংকড লিস্টের শেষ মাথায় চলে যেত।
এখন কিভাবে আমরা সাইকেলের প্রথম নোডটা খুজে বের করবো?
$m = $রুট নোড থেকে সাইকেলের প্রথম নোডের দূরত্ব
$k = $সাইকেলের প্রথম নোড থেকে খরগোশ ও কচ্ছপের মিটিং পয়েন্টের দূরত্ব
$l = $সাইকেলের দৈর্ঘ্য
এখন যদি কচ্ছপ মোট $c_{T}$ বার সাইকেলে চক্কর খেয়ে খরগোশের সাথে মিলিত হয় তাহলে কচ্ছপের অতিক্রম করা মোট দূরত্ব হবে:
$D_{T} = m + c_{T}*l + k$
খরগোশ যদি $c_{H}$ বার সাইকেলে চক্কর খেয়ে কচ্ছপের সাথে মিলিত হয় তাহলে খরগোশের অতিক্রম করা মোট দূরত্ব হবে:
$D_{H} = m + c_{H}*l + k$
যেহেতু খরগোশের গতি কচ্ছপের দ্বিগুণ তাই আমরা বলতে পারি:
$2*(m + c_{T}*l + k) = m + c_{H}*l + k$
এটাকে একটু ঘুরিয়ে লেখা যায়:
$m + k = (c_{H} – 2*c_{T})*l$
$l$ হলো সাইকেলের দৈর্ঘ্য, তারমানে $m + k$ হলো সাইকেলের দৈর্ঘ্যের একটা গুণিতক। আর সেটার মানে হলো যদি তুমি সাইকেলের প্রথম নোড থেকে $m+k$ দৈর্ঘ্য অতিক্রম করো তাহলে তুমি আবার প্রথম নোডে ফিরে আসবে। এটা বোঝাই এই অ্যালগোরিদমের সবথেকে গুরুত্বপূর্ণ অংশ।
এখন যদি তুমি মিটিং পয়েন্ট থেকে $m$ ঘর সামনে যাও তাহলেই তুমি সাইকেলের প্রথম নোডে আবার ফিরে আসবে, কারণ প্রথম নোড থেকে মিটিং পয়েন্টের দূরত্ব $k$। কিন্তু তুমি $m$ বা $k$ কারো মান ই জানো না, তাহলে কিভাবে $m$ ঘর সামনে যাবে? সেটার জন্য খুবই সহজ আর মজার একটা উপায় আছে। তোমার নিশ্চয়ই মনে আছে যে রুট নোড থেকে সাইকেলের প্রথম নোডের দূরত্বও $m$।
মনে করো খরগোশ এখন আর নেই, কিন্তু রুট নোড এ নতুন একটা কচ্ছপ পয়েন্টার $T2$ হাজির হয়েছে, আর $T$ সেই আগের মিটিং পয়েন্টেই আছে। এখন দুটি পয়েন্টারকেই এক ঘর করে আগাতে থাকলে তারা যেখানে মিলিত হবে সেটাই সাইকেলের প্রথম নোড!
এটাই হলো ফ্লয়েডের সাইকেল ডিটেকশন অ্যালগোরিদম। টাইম কমপ্লেক্সিটি এখনও O(n) ই আছে (কেন ?) কিন্তু মেমরি কমপ্লেক্সিটি হয়ে গেছে O(1)।
একটি সি++ কোড দেখি:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
/** * Definition for singly-linked list. * struct ListNode { * int val; * ListNode *next; * ListNode(int x) : val(x), next(NULL) {} * }; */ ListNode* Solution::detectCycle(ListNode* A) { if(!A->next)return NULL; ListNode *tortoise=A; ListNode *hare=A; //check if there is a cycle while(hare){ if(hare->next and hare->next->next) hare=hare->next->next; else return NULL; //no cycle tortoise=tortoise->next; if(hare==tortoise)break; //cycle exists } ListNode* tortoise2 = A; while(tortoise2 != tortoise){ tortoise2 = tortoise2->next; tortoise = tortoise->next; } return tortoise; } |
লিংকড লিস্টে সাইকেল ডিটেক্ট করা ছাড়াও এই অ্যালগোরিদম অনেক কাজে লাগে। যেমন কোনো গাণিতিক ফাংশন বা pseudo-random নাম্বার জেনারেটরের সাইকেল ডিটেক্ট করা।
অ্যালগোরিদমটা তুমি বুঝেছো নাকি পরীক্ষা করতে uva 350 pseudo random numbers সমস্যাটা সমাধান করতে পারো।
হ্যাপি কোডিং!
ফেসবুকে মন্তব্য
Powered by Facebook Comments





In the code, I think “if(!A->next)return NULL;” should be like
“if(A->next)return NULL;”. Great article.