$-১৭$ কে $৫$ দিয়ে ভাগ করলে ভাগশেষ কত হয়? $২^{১০০০}$ কে $১৭$ দিয়ে ভাগ করলে ভাগশেষ কত হয় সেটা কি তুমি ওভারফ্লো এড়িয়ে নির্ণয় করতে পারবে? $O(n)$ এ পারলে $O(\log_2 {n})$ কমপ্লেক্সিটিতে পারবে? যদি কোনো একটি উত্তর “না” হয় তাহলে এই পোস্ট তোমার জন্য। তবে তুমি যদি মডুলার ইনভার্স বা এডভান্সড কিছু শিখতে পোস্টটি খুলো তাহলে তোমাকে আপাতত হতাশ করতে হচ্ছে।
সি/জাভা সহ বেশিভাগ প্রোগ্রামিং ল্যাংগুয়েজে এ $\%$ কে ভাগশেষ অপারেটর ধরা হয়। $x$ কে $m$ দিয়ে ভাগকরে ভাগশেষ বের করার অর্থ $x\%m$ এর মান বের করা অথবা আমরা বলতে পারি $x$ কে $m$ দিয়ে mod করা। “determine answer modulo 1000” এ কথাটির অর্থ হলো উত্তরকে $১০০০$ দিয়ে mod করে তারপর আউটপুট দিতে হবে।
একটি সমস্যা দিয়ে শুরু করি। তোমার ১০০টি বই আছে,তুমি কয়ভাবে বইগুলো সাজাতে পারবে? খুব সহজ,$১০০!$ (১০০ ফ্যাক্টরিয়াল) ভাবে সাজাতে পারবে। ১০০! ১৫৮ ডিজিটের বিশাল একটি সংখ্যা। তাই আমি তোমাকে প্রবলেমটা সহজ করে দিলাম,ধরো তুমি $x$ উপায়ে বইগুলো সাজাতে পারবে,তাহলে তোমাকে $x%97$ কত সেটা বলতে হবে। অর্থাত ১০০! বের করে $৯৭$ দিয়ে ভাগ করে ভাগশেষটা বের করাই তোমার সমস্যা। (Determine 100 factorial modulo 97)
এটা কিভাবে করবে? $১০০!$ এর মান তুমি বের করতে পারবেনা $৬৪$বিট আনসাইনড ইন্টিজার দিয়েও, এরা $২^{৬৪}-১$ পর্যন্ত সংখ্যা নিয়ে কাজ করতে পারে, তাই ওভারফ্লো হবে। কিন্তু আমরা জানি আমাদের উত্তর কখনোই 97 এর বড় হবেনা কারণ কোনো সংখ্যাকে m দিয়ে mod করা হলে সংখ্যাটি m এর থেকে বড় হতে পারবেনা।
আমরা এ ধরণের সমস্যা সমাধান করতে সাহায্য নিবো দুটি সুত্রের:
$(a+b)\%m=((a\%m)+(b\%m))\%m$
$(a*b)\%m=((a\%m)*(b\%m))\%m$
$n$ সংখ্যক নম্বর $a_1,a_2…a_n$ এর জন্য সুত্র দুটি ব্যবহার করতে পারবে।
উপরের সমস্যাটিতে ২য় সুত্রটি লাগবে। তোমার বের করা দরকার ১০০! %৯৭ অর্থাত:
(১০০*৯৯*৯৮*………..*১)%৯৭
তুমি যেটা করবে সেটা হলো গুণ করার সময় ২য় সুত্রের মত করে mod করতে থাকবে,তাহলে কোনো সময়ই overflow ঘটবেনা কারণ mod করলে প্রতি স্টেপে সংখ্যাটি ছোটো হয়ে যাচ্ছে। এটার কোড হতে পারে এরকম:
|
1 2 3 4 5 6 7 |
int fact=1; for(int i=1;i<=100;i++) { fact=((fact%97)*(i%97))%97; } printf("%d\n",fact); |
এটার আউটপুট আসবে ০। অর্থাত ১০০! % ৯৭ =০। একটু খেয়াল করলেই বুঝবে এখানে আমরা ২য় সুত্রটি প্রয়োগ করেছি ২টি করে সংখ্যা নিয়ে।
সুত্র দুটি কেনো কাজ করে সেটা জানা দরকার। আমি ১ম সুত্রটির প্রমাণ দেখাচ্ছি,২য়টিও একইভাবে করা যায়। প্রমানটি আমার নিজের মত করে করা।
ধরি (x+y)%৫ এর মান আমাদের বের করতে হবে। এখন যদি $x\%5=c_1$ আর $y\%5 = c_2$ হয়,তাহলে $x$ কে আমরা লিখতে পারি $5n_1+c_1$ এবং $y$ কে লিখতে পারি $5n_2+c_2$ যেখানে $n_1$ আর $n_2$ দুটি ইন্টিজার। এটা একদম বেসিক রুল,আশা করে বুঝতে সমস্যা হচ্ছেনা। এখন:
$(x+y)\%5$
= $(5n_1+c_1+5n_2+c_2)\%5$
= $(5n_1+5n_2+c_1+c_2)\%5 $ ——(১)
এখানে $5n_1+5n_2$ অবশ্যই $5$ এর মাল্টিপল,তাই আমরা লিখতে পারি
$5n_1+5n_2=5N$ যেখানে $N=n_1+n_2$
এবং $c_1+c_2=C$
তাহলে (১) থেকে পাচ্ছি:
$(5N+C)\%5$
এখন পরিস্কার বোঝা যাচ্ছে যে উত্তর হলো $C\%5$। $C$ কে আবার mod করতে হলো কারণ $c_1+c_2$ এর মান 5 এর থেকে বড় হতেই পারে। এখন
$((x\%5)+(y\%5))\%5$——–(২)
=$((5n1+c1)\%5)+((5n2+c2)\%5))\%5$
$(5n_1+c_1)\%5=c_1$
$(5n_2+c_2)\%5=c_2$
তাহলে ২ কে লিখতে পারি:
$(c_1+c_2)\%5 = C\%5$
তাহলে ১ম সুত্রটি প্রমাণিত হলো। তারমান যোগ করে mod করা আর আগে mod করে তারপর যোগ করে আবার mod করা একই কথা। সুবিধা হলে সংখ্যাটি কোনো স্টেপেই বেশি বড় হতে পারেনা। গুণের ক্ষেত্রেই একই সুত্র প্রযোজ্য।
নেগেটিভ সংখ্যার mod নিয়ে একটু আলাদা ভাবে কাজ করতে হয়। সি তে $-17 \% 5$ এর মান দেখায় -২। কিন্তু সচরাচর আমরা ভাগশেষের যে সংজ্ঞা ব্যবহার করি তাতে $x\%m = p$ হলে গাণিতিকভাবে
m এর সবথেকে বড় থেকে বড় মাল্টিপল যেটা $x$ এর থেকে ছোট সেই সংখ্যাটিকে $x$ থেকে বিয়োগ করলে যে সংখ্যাটি পাওয়া যায় সেটাই $p$।
যেমন $23 \% 5$ এর ক্ষেত্রে $৫ \times ৪=২০$ হলো $৫$ এর সবথেকে বড় মাল্টিপল যেটা $২৩$ এর থেকে ছোট,তাই $23 \% 5=23-(5 \times 4)=3$। $-17 \% 5$ এর ক্ষেত্র খেয়াল করো $-20$ হলো $৫$ এর সবথেকে বড় মাল্টিপল যেটে $-১৭$ থেকে ছোট,তাই উত্তর হবে $৩$।
এই কেসটা handle করা একটি উপায় হলো নেগেটিভ সংখ্যাটিকে একটি $5$ এর মাল্টিপল এর সাথে যোগ করা যেন সংখ্যাটি ০ থেকে বড় হয়ে যায়,তারপরে mod করা। যেমন:
-17%5
=(-17+100)%5
=83%5
=3
এটা উপরের সুত্রের প্রমাণের মত করেই কাজ করে,একটু গুতালেই প্রমাণ করতে পারবে। নেগেটিভ সংখ্যার mod নিয়ে কনটেস্টে সবসময় সতর্ক থাকবে,এটা wrong answer খাওয়ার একটা বড় কারণ হতে পারে।
এবার আসি সুপরিচিত big mod সমস্যায়। সমস্যাটি হলো তোমাকে $(a^b)\%m$ এর মান বের করতে হবে, $a$,$b$,$m$ তোমাকে বলে দেয়া হবে,সবগুলোর range 2^31 পর্যন্ত হতে পারে। ১০০! % ৯৭ বের করার মত করে সহজেই তুমি overflow না খেয়ে মানটি বের করতে পারবে,সমস্যা হলো তুমি লুপ চালিয়ে একটি একটি গুণ করে $2^{2000000000}%101$ বের করতে চাইলে উত্তর পেতে পেতে সম্ভবত নাস্তা শেষ করে আসতে পারবে। আমরা চাইলে $O(\log_2{n})$ এ এটা করতে পারি।
লক্ষ করো
$2^{100}$
=$(2^{50})^2$
এবং
$(2^{50})$
=$(2^{25})^2$
এখন বলো $2^{50}$ বের করতে কি $2^{26}$, $2^{27}$ ইত্যদি বের করার দরকার আছে নাকি $2^{25}$ পর্যন্ত বের করে square করে দিলেই হচ্ছে? আবার $2^{25}$ পর্যন্ত আসতে $(2^{12})^2$ পর্যন্ত বের করে square করে সাথে ২ গুণ করে দিলেই যথেষ্ট,অতিরিক্ত ২ গুণ করছি সংখ্যাটি বিজোড় সে কারণে। প্রতি স্টেপে গুণ করার সময় mod করতে থাকবে যাতে overflow না হয়। recursion ব্যবহার করে কোডটি লেখা জলের মত সোজা:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
#define i64 long long i64 M; i64 F(i64 N,i64 P) { if(P==0) return 1; if(P%2==0) { i64 ret=F(N,P/2); return ((ret%M)*(ret%M))%M; } else return ((N%M)*(F(N,P-1)%M))%M; } |
মন্তব্য অংশে “হাসান” একটি বিগ মডের সুন্দর রিকার্শন-ট্রি এর ছবির লিংক দিয়েছে, ছবিটা এরকম:
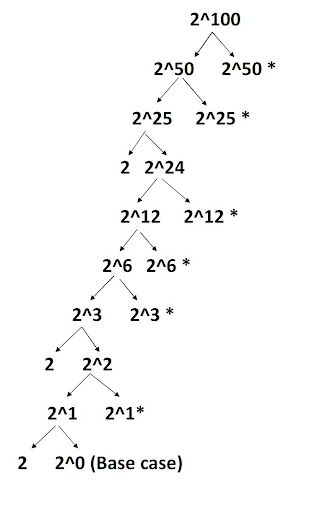
মডুলার অ্যারিথমেটিক ব্যবহার করে বিশাল আকারের ফলাফল কে আমরা ছোট করে আনতে পারি ফলাফলে বিভিন্ন প্রোপার্টিকে নষ্ট না করে,তাই এটা গণিতে খুব গুরুত্বপূর্ণ। প্রোগ্রামিং কনটেস্টে প্রায়ই বিভিন্ন প্রবলেমে মডুলার অ্যারিথমেটিক প্রয়োজন পড়বে,বিশেষ করে counting আর combinatorics এ যেখানে ফলাফল অনেক বড় হতে পারে,ফ্যাক্টরিয়াল নিয়ে কাজ করতে হতে পারে।
ভাগ করার সময় গুণ,আর যোগের মত সুত্র দুটি কাজ করেনা,এটার জন্য তোমাকে extended euclid আর modular inverse জানতে হবে।
সিপিউর জন্য mod খুব costly একটা অপারেশন। যোগ,গুণের থেকে mod করতে অনেক বেশি সময় লাগে। অপ্রয়োজনে mod ব্যবহার করলে কোড time limit exceed করতে পারে,তাই overflow হবার আশংকা না থাকলে সব জায়গায় mod করা দরকার নেই। আমার একটি কোড ৩সেকেন্ডে time limit exceed হবার পর খালি কিছু mod সরিয়ে ১.৩ সেকেন্ড নামিয়ে এনেছি।
এখন চিন্তা করার জন্য একটি প্রবলেম। ধরো তোমাকে একটি অনেক বড় সংখ্যা(bigint) দিয়ে সেটাকে $২^{৩১}$ এর ছোট একটি সংখ্যা দিয়ে mod করতে বলা হলো। $O(length\_of\_bigint)$ কমপ্লেক্সিটিতে কিভাবে করবে?
সাহায্য:
২৩=(০*১০+২)*১০ + ৩
১২৩৯=(((০*১০+১)*১০ + ২)*১০ +৩)*১০+৯
প্র্যাকটিসের জন্য প্রবলেম:
http://uva.onlinejudge.org/external/3/374.html
http://uva.onlinejudge.org/external/101/10127.html
ফেসবুকে মন্তব্য
Powered by Facebook Comments

i64 দিয়ে কি বুঝিয়েছেন? long long int ব্যবহার করবো?
i64 দিয়ে long long বুঝানো হয়েছে।
ভাইয়া, ট্রি টা কি এই রকম হবে?
https://picasaweb.google.com/271emtiaj/UntitledAlbum#5767638674915293362
হ্যা এরকমই হবে,ভালো হয়েছে ছবিটা।
vai tree ta jodi apni ai page add kore den khub valo hobe.Bz oi link e giye tree ta dekha jacce na.
tree ta page add korle vlo hoy
শাফায়েত ভাই আপনি মডুলার ইনভার্স নিয়ে কিছু লিখলে ভালো হয়।
[[কমেন্টটি বাংলায় লিখে দিলাম, ইংরেজি ফন্টে বাংলা কমেন্ট ভবিষ্যতে approve করা হবে না — শাফায়েত]]
চেষ্টা করবো তবে আমার লেখার অপেক্ষায় না থেকে একটু ঘাটাঘাটি করে শিখে ফেলো।
ভাইয়া ক্যালকুলেটর ইউচ করলে তো -১৭%৫= ২ আসে। মানে আমি করেছি এভাবে -১৭/৫ = -৩ সমস্ত ২ বাই ৫ । কিন্তু আপনি দ্যাখালেন -১৭%৫= ৩ । আমি আসলে এই ব্যাপারটা নিয়ে কনফিউসড । বিভাজ্যতার নিয়ম অনুযায়ী তো আপনি ঠিক আছেন, তাহলে ক্যালকুলেটর কি ভুল? নাকি দুটই ঠিক আছে, আমারি বুঝতে কোথাও প্রব্লেম হচ্ছে !
আমিতো আমার উবুন্টুর ক্যালকুলেটরে “−17 mod 5” লিখে ৩ পাচ্ছি।
ভাইয়া এমনিতে ক্যালকুলেটর চেপে ভাগ করেন -১৭/৫ = -৩.৪ । আর -৩.৪ মানে তো “-৩ সমস্ত ২ বাই ৫” । অর্থাৎ অবশেষ ২ । আমার বোঝায় কি কোথাও সমস্যা আছে?
ব্যাপারটা আসলে ঠিক সেরকম না। ধরো একটা সংখ্যা x । n এর যে মাল্টিপলটা x এর সবথেকে কাছাকাছি পৌছায় কিন্তু x এর সমান বা ছোট সেই মাল্টিপল থেকে x এর ডিফারেন্সটাই ভাগশেষ। ৫ এর কোন মাল্টিপল -১৭ এর সবথেকে কাছাকাছি? অবশ্যই -২০। -১৫ না কারণ এটা -১৭ এর থেকে বড়। -২০ আর -১৭ এর পার্থক্য ৩ তাই ভাগশেষ ৩।
তাহলে ব্যাপারটা দাড়ালো,
যদি বলা হয় -১৭/৫ এর মান কত? উত্তর হবে -৩.৪ [মানে এখানেঃ ভাজ্য, ১৭ = -(৫X৩+২)]
আর -১৭/৫ এর ক্ষেত্রে ভাগশেষ কত, তাহলে উত্তর হবে ৩ [মানে এখানেঃ ভাজ্য, ১৭ = ৫X(-৪)+৩]
ব্যাপারটা কেমন জানি সাংঘর্ষিক হয়ে গেলো না ভাইয়া?
ব্যাপারটা আসলে এই রকম না। আমরা জানি যে ভাজ্য = ভাজক * ভাগফল + ভাগশেষ। আর এখানে এইটাই হয়েছে। -১৭ = ৫ * (-৪) + ৩ । এখানে ভাজ্য = -১৭ , ভাজক = ৫ , ভাগফল = -৪ ও ভাগশেষ = ৩ । আর একটা জিনিস সেটা হচ্ছে ভাগশেষ কখনো ঋণাত্মক হয় না @Shikhor Kumer Roy ভাই
তুমি ফেইসবুকের মাধ্যমে মাসুম বিল্লাল যে কমেন্টটা দিয়েছে সেটা খেয়াল কর।
(ভাইয়া আসলে গাণিতিকভাবে -৯%১২=-৯ অথবা ৩। কোনটাই ভুল না। তবে কম্পিউটারের বুদ্ধি নাই যে সে এইটাকে ৩ হিসেবে বলবে 🙂 আসলে ব্যাপারটা হইতেছে -৯ কে এইভাবে দেখেন, ১২ থেকে ৩ সরে আসছে।.)
আর দেখ এটা–
মনে কর তোমার কাছে এমন একটা ঘড়ি আছে যেটাতে 12 ঘন্টার জায়গায় মাত্র 5 টা ঘন্টা আছে। এদের মার্ক দেয়া 0, 1, 2, 3, 4. জিরো থেকে শুরু করে ঘড়ির কাটাঁর দিকে ঘুরে তুমি যদি বারো ঘর এগোও তাহলে তুমি 2 এ পৌঁছাবা।
গাণিতিকভাবে আসলেই ব্যপারটা হয়-
12 Ξ 2 (mod 5).
এখন তুমি যদি ঘড়ির কাটাঁর বিপরীত দিকে 12 বার ঘুরে আসো তবে তুমি 3 এ এসে পৌঁছাবা।
– 12 Ξ 3 (mod 5).
@Shikhor Kumar Roy
I am grateful to you.When i have not found any effective way to learn algorithm & programming, this is the blog which inspires me to learn algorithm & programming and i enjoy this blog and tutorial every moment.
thanks
🙂
খুব ভালো লাগলো ,ভাইয়া ।
ভাইয়া ,এখানে long long এর জায়গায় i64 ব্যবহার করার কি দরকার ছিল ?
আসলে আমি কোডে সবসময় #define i64 long long এই লাইনটা ব্যবহার করি, i64 আর long long তাই এখানে একই জিনিস।
ভাইয়া প্রথম প্রব্লেমটাতে wrong answer আসতেছে । বুঝতেছিনা কোথায় ভুল করলাম
#include
using namespace std;
long long int modu(long long int b,long long int p,long long int m)
{
if(p==0)
return 1;
if(p%2==0)
{
long long int t=modu(b,p/2,m);
//return (modu(b,p/2,m)*modu(b,p/2,m))%m;
return (t*t)%m;
}
else
return ((b%m)*modu(b,p-1,m))%m;
}
int main()
{
long long int b,p,m;
cin>>b>>p>>m;
cout<<modu(b,p,m);
return 0;
}
১১ নাম্বার লাইনে ,
(t*t) %m এই লাইনটা ওভারফ্লো হতে হতে পারে,
(t%m * t%m) %m লাইনটা এমন হবে
ভাইয়া, রিকারসনের কোড টিতে M,N এবং P ভ্যরিয়াবল গুলার কাজ কি আমি বুযিনাই 🙁 , দয়াকরে একটু ক্লিয়ার করে বলবেন প্লিজ? 🙂
আমরা এখানে (N^P)%M বের করছি।
ভাইয়া, শেষ কোডটাতে fn() ফাংশনে N parameter হিসাবে নেওয়ার দরকার নাই। Global variable হিসাবে নিলেই চলে। কারণ পুরো fn() ফাংশনে N এর কোনো পরিবর্তন নাই। এটা ঠিক করলে ভালো লাগবে দেখতে।
আমার দেখা সবচেয়ে গোছানো সাইট এটা। Thank you for this.
ধন্যবাদ তোমাকে। লোকাল ভ্যারিয়েবল নেয়ার কিছু সুবিধা আছে, ভ্যারিয়েবলের স্কোপটা ওই ফাংশনের মধ্যেই সীমাবদ্ধ থাকে, অন্য কোথাও একই নামের ভ্যারিয়েবল ব্যবহার করতে সমস্যা হয় না। গ্লোবাল ভ্যারিয়েবল বেশি ব্যবহার করলে কোডে বাগ তৈরির সম্ভাবনা বাড়ে :)।
হুম। বুঝলাম। এখন থেকে Global variable avoid করারার চেষ্টা করব। 🙂
ভাইয়া,চিন্তা করার জন্যে যে প্রবলেমটি দিয়েছেন,সেটা বুঝতেছি না,যদি ক্লিয়ার করতেন,তবে বেশ উপকার হতো!
viya onek upokrito holam . onek donnobad