রিকার্শন ব্যবহার করতে গেলে অনেক সময় দেখা যায় রিকার্শনের গভীরতা অনেক বেশি হয় গেলে মেমরি শেষ হয়ে যায় এবং কোড ক্র্যাশ করে। আমরা আজকে একটি অপটিমাইজেশন টেকনিক শিখবো যেটা ব্যবহার করে কোনো কোনো সময় রিকার্শনের মেমরি ব্যবহার অনেক কমিয়ে আনা সম্ভব।
প্রথমে জানা দরকার টেইল-কল (Tail call) জিনিসটা কি। সহজভাবে বলতে গেলে, টেইল-কল হলো একটা ফাংশনের শেষ লাইন। অর্থাৎ যে কাজটি করার পর ফাংশনের আর কোনো কাজ থাকে না সেটাই টেইল-কল। যেমন নিজের ফাংশনটি দেখ:
|
1 2 3 4 5 6 7 8 9 10 11 |
int mod = 1000007; int fact(int n) { int ans = 1; for (int i = 1; i <= n; i++) { ans = (ans * i) % mod; } return ans; } |
এটা ফ্যাক্টরিয়াল বের করার একটি ফাংশন। এই ফাংশনে return ans এর পর ফাংশনটির আর কোনো কাজ নেই, তাই এটাই হলো টেইল-কল।
mod কেন ব্যবহার করছি? কারণ আমরা অনেক বড় $n$ ব্যবহার করবো কিন্তু আমরা চাইনা ইন্টিজার ওভারফ্লো হোক।
এখন এই ফাংশনটাকেই আমরা রিকার্শন ব্যবহার করে লিখবো:
|
1 2 3 4 5 6 7 8 9 |
int mod = 1000007; int fact(int n) { if (n == 0) { return 1; } int ret = (n * fact(n - 1) % mod); } |
একটা রিকার্শিভ ফাংশনকে টেইল-রিকার্শন বলা হয় যদি রিকার্সিভ কল করা টাই হয় এই ফাংশনের শেষ কাজ। উপরের ফাংশনটির শেষ কাজ হলো $n * fact(n-1)$ এর মান রিটার্ণ করা। তারমানে শেষ কাজ হলো রিকার্সিভলি $fact(n – 1) $ কে কল করা? তুমি যদি রিকার্সন কিভাবে কাজ করে সেটা বুঝে থাকো তাহলে এতক্ষণে বুঝে গেছো যে এটা শেষ কাজ না! ফাংশনটি প্রথমে $fact(n-1)$ এর মান রিকার্সিভলি বের করে আনবে, এরপর সেটাকে $n$ দিয়ে গুণ করবে। আমরা চাইলে নিচের মতো করে লিখতে পারি:
|
1 2 3 4 5 6 7 8 9 10 |
int mod = 1000007; int fact(int n) { if (n == 0) { return 1; } int ret = fact(n - 1); return (n * ret) % mod; } |
একই ফাংশন, শুধু শেষ লাইনটা একটু ভেঙে লিখেছি। এখান থেকে বোঝা যাচ্ছে এই ফাংশনটা টেইল-রিকার্শন না, শেষ লাইনে আমরা রিকার্সিভ ফাংশন কল করছি না, বরং আগের লাইনে রিকার্সিভ ফাংশন কল করে শেষ লাইনে সেটা ব্যবহার করে ক্যালকুলেশন করছি।
এখন তুমি এই ফাংশনটা ব্যবহার করে $fact(1000000)$ এর মান প্রিন্ট করা চেষ্টা করো (আমি ধরে নিচ্ছি তুমি কোনো সেটিং পরিবর্তন করে মেমরি বাড়িয়ে নিচ্ছো না)। আমি যখন $fact(1000000)$ রান করলাম, সাথে সাথে প্রোগ্রাম ক্র্যাশ করলো আর দেখালো segmentation fault। তারমানে প্রোগ্রামটি অনেক বেশি মেমরি ব্যবহার করেছে এবং ক্র্যাশ করেছে। তুমি জিজ্ঞেস করতে পারো আমিতো কোনো অ্যারে ব্যবহার করিনি, কিভাবে এই কোড এত বেশি মেমরি খরচ করে ফেললো?
প্রতিটি ফাংশন একটা মেমরি স্পেসে রান করে। তুমি যখন রিকার্সিভলি একই ফাংশন কল করো তখন একই মেমরি স্পেসে নতুন প্যারামিটার ব্যবহার করে ফাংশনটা আবার রান করে এবং ফিরে আসার পর পুরানো প্যারামিটার ব্যবহার করে বাকি কাজ শেষ করে।
ধরো তুমি $fact(3)$ বের করতে চাও। লাইন ৮ এ গিয়ে কোডটা একই ফাংশন কল করবে $n = 2$ ব্যবহার করে। তারমানে একই মেমরি স্পেসে নতুন প্যারামিটার $n = 2$ ব্যবহার করে ফাংশনটা এখন রান করবে। এরপর একসময় ফিরে এসে লাইন ৯ এ বাকি ক্যালকুলেশন করবে পুরানো প্যারামিটার ব্যবহার করে। যেহেতু একই মেমরি স্পেস ব্যবহার হচ্ছে, ফিরে আসার পর প্রসেসটা কিভাবে জানবে যে $n$ এর মান আগে কত ছিলো?
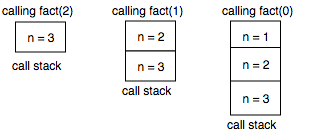
এটা জানতে ইন্টার্নালি একটা স্ট্যাক ব্যবহার করা হয়। যতবার তুমি রিকার্সিভ কল করো, স্ট্যাকে পুরানো প্যারামিটার গুলো সেভ করে রাখা হয়। নিচের ছবি দেখো:
যখন $fact(3)$ থেকে $fact(2)$ কে কল করা হচ্ছে তখন $n = 3$ কে স্ট্যাকে সেভ করে রাখা হচ্ছে। ঠিক সেভাবে $n = 1$ কল করার সময় $n = 2$ কে স্ট্যাকে সেভ করে রাখা হচ্ছে। এভাবে সেভ করে রাখার কারণে রিকার্সিভ কল শেষ করে ফিরে আসার সময় স্ট্যাকের উপরে আগের ফাংশন কলের প্যারামিটার গুলো খুজে পাওয়া যায় সহজেই। (বিস্তারিত জানতে স্ট্যাক নিয়ে আমার এই লেখাটা পড়তে পারো।
তুমি যখন $fact(n)$ কল করছো তখন স্ট্যাকে এভাবে করে $n$ টি এন্ট্রি সেভ করে রাখতে হচ্ছে। সি++ এ রিকার্সন কত মেমরি ব্যবহার করতে পারবে তার একটি লিমিট আছে। $n$ এর মান যখন অনেক বড় তখন মেমরির ব্যবহার লিমিটের বাইরে চলে যাচ্ছে আর কোড ক্র্যাশ করছে।
আমরা যদি এই মেমরি ব্যবহার কোনোভাবে কমাতে পারি তাহলে কোড ক্র্যাশ করবে না। বর্তমানের কম্পাইলারগুলো খুবই বুদ্ধিমান, সে যদি দেখে যে অতিরিক্ত মেমরি ব্যবহার দরকার নেই তাহলে সে এমনভাবে অপটিমাইজড মেশিন কোড জেনারেট করে যাতে মেমরি ব্যবহার কম হয়। আমরা সেই বুদ্ধিটাই কাজে লাগাবো।
আগের কোডে আমাদেরকে পুরানো প্যারামিটারগুলো স্ট্যাকে সেভ করতে হয়েছে কারণ ফিরে আসার পর সেগুলো কাজে লাগবে। আমরা কি এমনভাবে কোডটা লিখতে পারি যাতে ফিরে আসার পর পুরানো প্যারামিটার আর কোনো দরকার নেই? এখানেই টেইল-কল এর আইডিয়া কাজে লাগবে। আমরা এমন ভাবে কোডটা লিখবো যাতে রিকার্সিভ ফাংশন কল করার পর আর কোনো কাজ করা না লাগে, তাহলে স্ট্যাকে $n$ এর মানগুলো সেভ করে রাখা দরকার হবে না।
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
int mod = 100007; int fact_tail(int n, int result) { if (n == 0) { return result; } return fact_tail(n - 1, (n * result) % mod); } int fact_optimized(int n) { return fact_tail(n, 1); } |
এবার আমরা প্রতিবার রিকার্সিভ কল শেষ হবার পর রেজাল্ট ক্যালকুলেশন না করে আমরা প্রতিবার আংশিক একটা রেজাল্ট ক্যালকুলেট করে সেটাকে প্যারামিটার হিসাবে পাঠিয়ে দিচ্ছি। একদম শেষে গিয়ে ওই প্যারামিটারেই আমরা ফলাফল পেয়ে যাবো।
|
1 2 3 4 5 6 |
fact(4, 1) = fact(3, 4 * 1) = fact(2, 4 * 3) = fact(1, 4 * 3 * 2) = fact(0, 4 * 3 * 2 * 1) = fact(0, 24) |
এইটা একটা টেইল রিকার্শন, কারণ শেষ লাইনে রিকার্সিভ ফাংশন কল করার পরে আর কোনো কাজ করা হয় নি। এই কোড যখন কম্পাইল করা হবে তখন কম্পাইলার দেখবে স্ট্যাক ব্যবহার করে পুরানো মান সেভ করে রাখার কোনো দরকার নেই। তাই এই কোডে ততটুকুই মেমরি লাগবে যতখানি লাগতো সাধারণ লুপ ব্যবহার করলে!
আধুনিক যেকোন ল্যাংগুয়েজের কম্পাইলার এই অপটিমাইজেশনটা করতে পারে। তুমি যদি সি/সি++ ব্যবহার করো তাহলে প্রোগ্রাম রান করার আগে তুমি দেখো -O2 কম্পাইলার অপটিমাইজেশন চালু করা আছে নাকি, না থাকলে আগে চালু করে দাও, তুমি যে কোড এডিটর ব্যবহার করছো সেখানে চালু করার অপশন থাকবে। অথবা তুমি সরাসরি টার্মিনাল থেকেও কম্পাইল করতে পারো -O2 অপশন ব্যবহার করে। কিভাবে করতে হয় গুগলে সার্চ দিয়ে দেখে নাও। (প্রোগ্রামিং কনটেস্টে জাজ মেশিনে সাধারণত এই অপটিমাইজেশন চালু করা থাকে)
এবার fact_optimized(1000000) রান করে দেখো সুন্দর আউটপুট দিচ্ছে।
এটাই হলো রিকার্শনের টেইল-কল অপটিমাইজেশন।
এক্সারসাইজ ১
নিচের কোডটা একট অ্যারের সবগুলো সংখ্যার যোগফল বের করে:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
int find_sum(int * numbers, int index) { if (index == 0) { return numbers[0]; } return numbers[index] + find_sum(numbers, index - 1); } int main() { int numbers[] = {5, 10, 15, 20}; int n = 4; cout<<find_sum(numbers, n - 1)<<endl; } |
এই কোডটাকে রিকার্সিভলি আগের সংখ্যাগুলোর যোগফল বের করে বর্তমান সংখ্যার সাথে যোগ করা হচ্ছে। তোমার কাজ হবে টেইল-কল রিকার্শন ব্যবহার করা যাতে করে রিকার্সিভ ফাংশন কল করার পর আর কোনো ক্যালকুলেশন করা না লাগে।
এক্সারসাইজ ২
ফিবোনাচ্চি সিরিজ হলো এমন একটি সিরিজ যার প্রতিটি সংখ্যা সিরিজের আগের দুটি সংখ্যার যোগফল। সিরিজের প্রথম দুটি সংখ্যা হলো 0 আর 1 এবং সিরিজের প্রথম কয়েকটি সংখ্যা হলো $0, 1, 1, 2, 3, 5, 8, 13, 21 …. $। একে নিচের ফাংশন দিয়ে প্রকাশ করা যায়:
|
1 2 3 |
fib(0) = 0 fib(1) = 1 fib(n) = fib(n - 1) + fib(n -2) where n > 1 |
সাধারণ ভাবে রিকার্সিভ ফাংশন লিখলে সেটা টেইল-কল রিকার্শন হবে না কারণ সেটা প্রথমে $fib(n – 1)$ এর মান বের করে ফিরে এসে আবার $fib(n – 2)$ বের করবে। তোমার কাজ $n$ তম ফিবোনাচ্চি বের করার জন্য টেইল-কল রিকার্শন লেখা।
ফেসবুকে মন্তব্য
Powered by Facebook Comments

int mod = 1000007;
int fact(int n) {
if (n == 0) {
return 1;
}
int ret = (n * fact(n – 1) % mod);
}
শেষ লাইনটায় return হওয়ার কথা।