(সবগুলো পর্ব) ম‍্যাট্রিক্স চেইন মাল্টিপ্লিকেশন আরেকটা ক্লাসিক ডাইনামিক প্রোগ্রামিং প্রবলেম যেখানে আমাদেরকে বের করতে হবে কিছু ম‍্যাট্রিক্সকে কিভাবে সবথেকে কম অপারেশন ব‍্যবহার করে গুণ করা যাবে।  ডিভাইড এন্ড কনকোয়ার পদ্ধতির খুবই চমৎকার একটা উদাহরণ এই প্রবলেমটা।

আমি আশা করবো ম‍্যাট্রিক্স কিভাবে গুণ করতে হয় সেটা সবাই জানো, আমি সেটা নিয়ে বিস্তারিত বলবো না। আমি খালি কয়েকটা প্রোপার্টির কথা মনে করিয়ে দিতে চাই। ধরা যাক আমাদের দুটি ম‍্যাট্রিক্স আছে $A_{1}$ এবং $A_{2}$ এবং তাদের ডাইমেনশন হলো $(r_{1} \times c_{1})$ এবং $(r_{2} \times c_{2})$।

• $A_{1}$ এবং $A_{2}$ গুণ করা যাবে শুধুমাত্র যদি $c_{1} = r_{2}$ হয়, অর্থাৎ প্রথম ম‍্যাট্রিক্সের কলাম, দ্বিতীয় ম‍্যাট্রিক্সের রো এর সমান হতে হবে।
• ম‍্যাট্রিক্সের অর্ডার গুরুত্বপূর্ণ। $A_{1} \times A_{2}$ আর $A_{2} \times A_{1}$ একই জিনিস না।
• ম‍্যাট্রিক্স দুটি গুণ $(A_{1} \times A_{2})$ করার পর যে নতুন ম‍্যাট্রিক্স পাবো তার ডাইমেনশন হবে $(r_{1} \times c_{2})$।
• ম‍্যাট্রিক্স দুটি গুণ করার সময় আমাদের কিছু সংখ‍্যাকে গুণ করে যোগ করতে হয় যেগুলোকে আমরা স্কেলার গুণ বলতে পারি। আমাদেরকে মোট স্কেলার গুণ করতে হবে $(r_{1} \times c_1 \times c_2)$ বার। কারণ নতুন ম‍্যাট্রিক্সে $(r_{1} \times c_{2})$ টা ঘর থাকবে এবং প্রতি ঘরে $c_1$ টা পেয়ার গুণ করতে হবে।

এখন ধরা যাক আমাদেরকে ৩টা ম‍্যাট্রিক্সের গুণফল $A_{1}  \times A_{2} \times A_{3}$ বের করতে হবে। এখন $col_{1} = row_{1}$ এবং $col_{2} = row_{3}$ হলেই শুধুমাত্র আমরা  গুণটা করতে পারবো। গুণটা দুই উপায়ে করা যায়:

• $(A_1 \times A_2) \times A_3$
• $A_1 \times (A_2 \times A_3)$

দুইটা উপায়ের পার্থক‍্য শুধু ব্রাকেটিং এ। দুই ক্ষেত্রেই আমরা $row_1 \times col_3$ ডাইমেনশনের একটা ম‍্যাট্রিক্স পাবো। কিন্তু দুইটা উপায়েই কি আমাদের একই সংখ‍্যক স্কেলার গুণ করা লাগবে? একটা উদাহরণ দেখি।

মনে করো ম‍‍্যাট্রিক্সগুলোর ডাইমেনশন হলো যথাক্রমে $(10 \times 100), (100 \times 5)$ এবং $(5 \times 50)$

• $(A_1 \times A_2) \times A_3$ ব্রাকেটিং এ স্কেলার গুণ করতে হবে $(10 \times 100 \times 5) + (10 \times 5 \times 50) = 7500$ বার।
• $A_1 \times (A_2 \times A_3)$ ব্রাকেটিং এ স্কেলার গুণ করতে হবে $(100 \times 5 \times 50) + (10 \times 100 \times 50) = 75000$ বার।

দ্বিতীয় উপায় শুরুতেই (A_2 \times A_3) গুণ করে বিশাল একটা ম‍্যাট্রিক্স বানিয়ে ফেলছি এবং ১০গুণ বেশি কমপ্লেক্সিটি বাড়িয়ে ফেলেছি।

বুঝতেই পারছো আমাদের উদ্দেশ‍্য হবে এখন স্কেলার গুণের সংখ‍্যা মিনিমাইজ করা। তোমাকে $n$ টা ম‍্যাট্রিক্স দেয়া থাকবে, বলতে হবে সর্বনিম্ন কয়টা স্কেলার গুণ অপারেশন ব‍্যবহার করে $A_1 \times A_2 \times ….. \times A_{n-1}$ বের করা যায়।

এখন প্রথম কাজ সাবপ্রবলেম বের করা। ধরে নিলাম সাবপ্রবলেম হলো $f(i)$ অর্থাৎ আমাদেরকে বের করতে হবে $i$ থেকে $n-1$ তম ম‍্যাট্রিক্সগুলো গুণ করতে মিনিমাম কয়টা অপারেশন লাগে। এখন মনে করো আমরা $i$ থেকে $k$ তম ম‍্যাট্রিক্সকে একটা ব্রাকেটের মধ‍্যে ফেলবো এবং $f(k + 1)$ প্রবলেমটা রিকার্সিভলি সলভ করবো।

কিন্তু এখন আমরা আরেকটা সমস‍্যায় পরে গিয়েছি, $i$ থেকে $k$ তম ম‍্যাট্রিক্সটুকুকে কিভাবে অপটিমালি গুণ করবো?

$cost(A_i \times A_{i+1} \times … \times A_j) + f(k + 1)$

আমাদের ফাংশন $f$ খালি $i$ থেকে অ‍্যারের শেষ পর্যন্ত অংশের জন‍্য কাজ করে, যে কোনো স‍্যাবঅ‍্যারে $[i, j]$ এর জন‍্য না। তাহলে কি করা যাবে? আমরা ফাংশনটাকে নতুন করে ডিফাইন করি: $f(i, j)$। এবার আমরা যেকোনো পজিশন $k$ এর জন‍্য অ‍্যারেটাকে দুই ভাগে ভাগ করে ফেলতে পারি।

যেমন $n = 4$ এর জন‍্য $f(0, 3)$ কে এভাবে ভাগ করা যায়:

• $k = 0$ ব্রাকেটিং -> ($A_{0}) \times (A_1 \times A_2 \times A_3)$ সাবপ্রবলেম -> $f(0,0) + f(1,3)$
• $k = 1$ ব্রাকেটিং -> $(A_{0}  \times A_{1}) \times (A_2 \times A_3)$ সাবপ্রবলেম -> $f(0,1) + f(2,3)$
• $k = 2$ ব্রাকেটিং -> $(A_{0}  \times A_{1} \times A_{2}) \times (A_3)$ সাবপ্রবলেম -> $f(0, 2) + f(3,3)$

অর্থাৎ আমরা যতভাবে সম্ভব অ‍্যারেটাকে দুইভাগে ভাগ করে ফেলবো এবং সাবপ্রবলেমগুলো রিকার্সিভলি সলভ করবো, প্রতিটা $k$ এর জন‍্য সাবপ্রবলেম হবে $f(i, k)$ এবং $f(k+1, n-1)$।

ম‍্যাট্রিক্সগুলো দুইভাগ করেই কিন্তু কাজ শেষ না, এবার মার্জ করতে হবে। $k$ তম পজিশনে ভাগ করলে তুমি বামে $row_{i} \times col_k$ সাইজের এবং ডানে $row_{k+1} \times col_{j}$ সাইজের ম‍্যাট্রিক্স পাবে যেখানে $col_k = row_{k+1}$। এবার এই দুইটি ম‍্যাট্রিক্সও গুণ করতে হবে এবং অপারেশন লাগবে $row_{i} \times col_k \times col_j$ টা।

$i$ তম ম‍্যাট্রিক্সের রো-কলামকে $mat[i].row$ এবং $mat[i].col$ হিসাবে লিখলে রিকার্সিভ ফর্মুলা হবে:

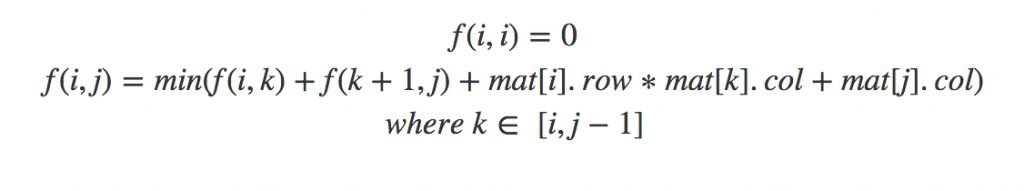ডিভাইড এন্ড কনকোয়ারে ২টা মুল কাজ থাকে, ডান আর বামের সাবপ্রবলেম ডিফাইন করা এবং মার্জ করা। আমরা মার্জ অপারেশনটাকে আলাদা ফাংশন হিসাবে ধরলে আরো পরিস্কার একটা ফর্মূলা লিখতে পারি:

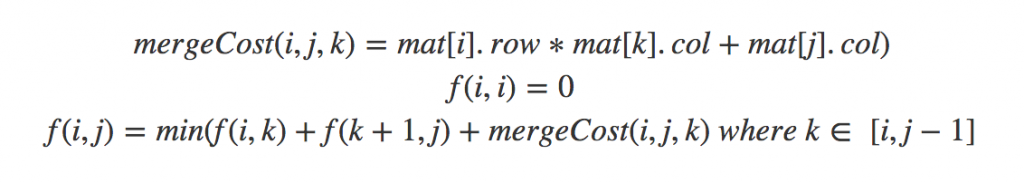এই প‍্যাটার্নটা মাথায় রাখলে আরো অনেক প্রবলেম সলভ করতে পারবে। এখন কোড দেখি:

কমপ্লেক্সিটি

আমাদের সাবপ্রবলেমের সংখ‍্যা $O(n^2)$ এবং প্রতিটা সাবপ্রবলেমে একটা $n$ সাইজের লুপ চালাচ্ছি। মোট কমপ্লেক্সিটি $O(n^3)$।

ইটারেটিভ ভার্সন

তুমি যদি আগের মত $i$ আর $j$ এর দুটো নেস্টেড লুপ চালিয়ে ইটারেশন করার চেষ্টা করো তাহলে এবার কাজ হবে না। $mem$ টেবিলটা কিন্তু এবার রো-বাই-রো বিল্ডআপ হচ্ছে না। এবার আমরা প্রথমে সবথেকে ছোট সাবঅ‍্যারেগুলোর জন‍্য আগে সলভ করবো যেমন $(0,0), (1,1), (2,2)$, এরপর করবো $1$ সাইজের সাবঅ‍্যারের জন‍্য, যেমন $(0,1), (1,2)$। এভাবে করে $1$ থেকে $n$ সাইজের সবগুলো সাবপ্রবলেমের সমাধান করবো। তাহলে টেবিলটা এবার বিল্ডআপ হবে কোনাকুনি:

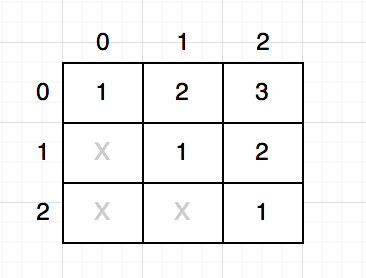ছবিতে কোন অর্ডারে টেবিল বিল্ডআপ হয়েছে দেখিয়েছি।

ইটারেটিভ ডিপিতে লুপের অর্ডারিংটা একবার বের করে ফেললে বাকিটা রিকার্সিভের মতোই। কর্নার কেস হ‍্যান্ডেল করার সুবিধার জন‍্য সরাসরি mem টেবিলে হাত না দিয়ে evaluate ফাংশনটা ব‍্যবহার করেছি।

প্র‍্যাকটিস প্রবলেম:

https://www.spoj.com/problems/MIXTURES/
https://leetcode.com/problems/burst-balloons/

আজ এই পর্যন্তই, হ‍্যাপি কোডিং। পরের পর্বে আমরা শিখবো বিটমাস্ক ব‍্যাবহার করে ট্রাভেলিং সেলসম‍্যান প্রবলেম কিভাবে সমাধান করতে হয়।

(সবগুলো পর্ব)