(অন্যান্য পোস্ট)
আগের পোস্টে আমরা প্রিমস অ্যালগোরিদম ব্যবহার করে mst নির্ণয় করা দেখেছি। mst কাকে বলে সেটাও আগের পোস্টে বলা হয়েছে। এ পোস্টে আমরা দেখবো mst বের করার আরেকটি অ্যালগোরিদম যা ক্রুসকালের অ্যালগোরিদম নামে পরিচিত। এটি mst বের করার সবথেকে সহজ অ্যালগোরিদম। তবে তোমাকে অবশ্যই ডিসজয়েন্ট সেট ডাটা স্ট্রাকচার সম্পর্কে জানতে হবে,না জানলে এই পোস্টটি অবশ্যই দেখে আসো।

এই পোস্টে নিজের আকা ছবি ব্যবহার করবোনা। উইকিতে ক্রুসকাল নিয়ে খুব সুন্দর করে লেখা আছে,আমি ওখানকার ছবিগুলোই ব্যবহার করে সংক্ষেপে অ্যালগোরিদমটা বুঝানোর চেষ্টা করবো।

নিচের গ্রাফটি দেখো:

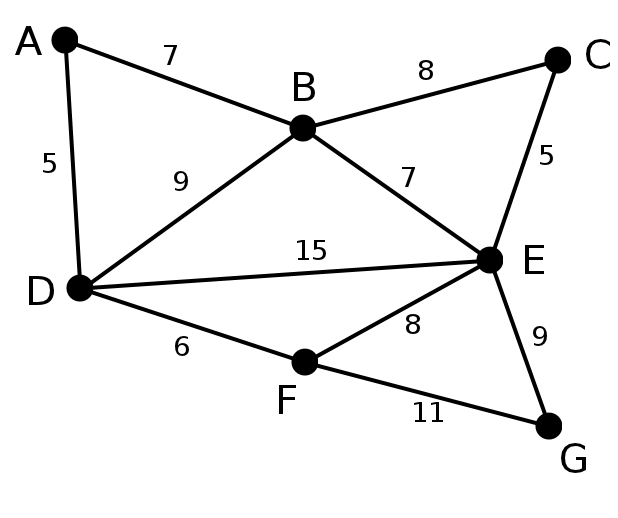
প্রথমে আমাদের ট্রিতে একটি এজও নেই। আমরা মুল গ্রাফের এজগুলোকে cost অনুযায়ী সর্ট করে ফেলবো। সব থেকে কম cost এর এজ আগে নিবো,বেশি cost এর এজ পরে নিবো। দুটি এজের cost সমান হলে যেকোনো একটি আগে নিতে পারি। তারপর একটি করে এজ নিবো আর দেখবো এজের দু প্রান্তের নোডগুলোর মধ্যে ইতোমধ্যে কোনো পথ আছে নাকি,যদি থাকে তাহলে এজটি নিলে সাইকেল তৈরি হবে,তাই এজটা আমরা নিবোনা। বুঝতেই পারছো প্রিমসের মত এটিও একটি ‘গ্রিডি’ অ্যালগোরিদম।

উপরে AD আর CE হলো সবথেকে কম cost এর এজ। আমরা AD কে সাবগ্রাফের অন্তর্ভূক্ত করলাম।

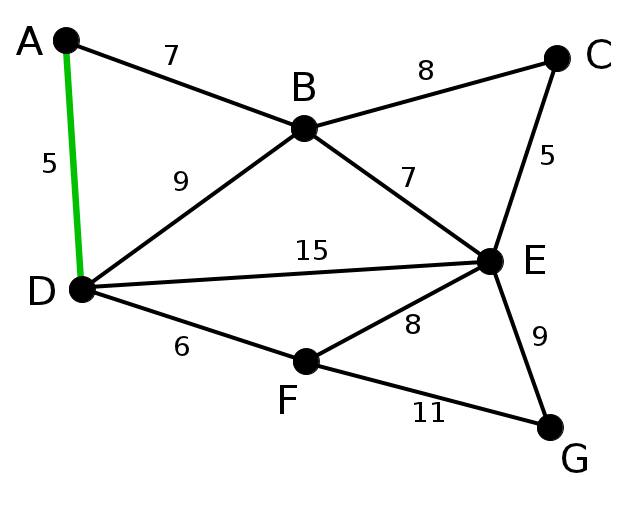
একই ভাবে এরপ CE তারপর DF,AB এবং BE কে যোগ করবো:

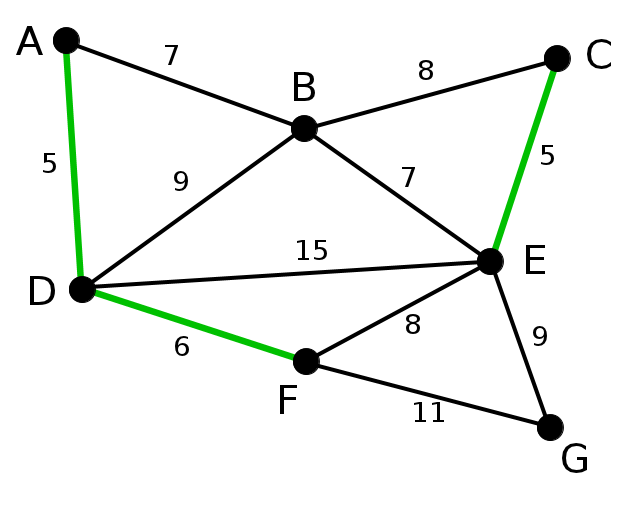
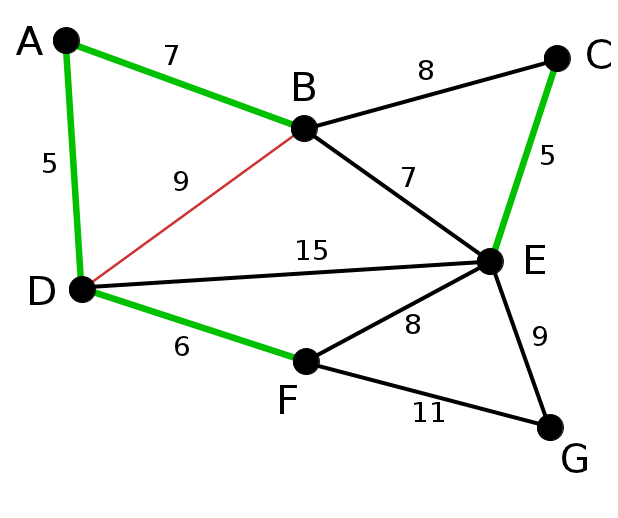
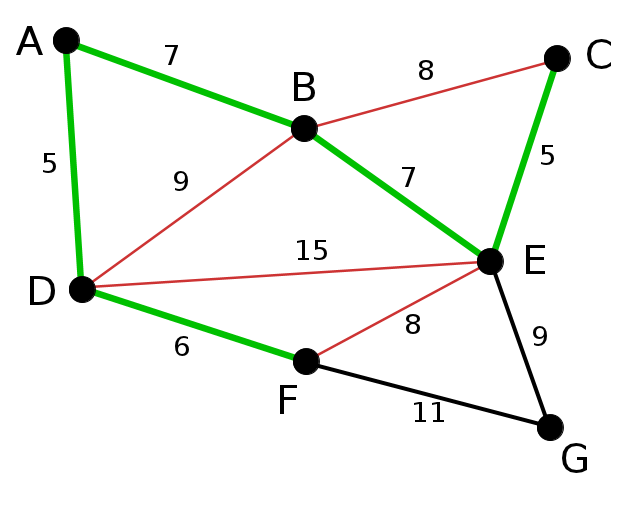
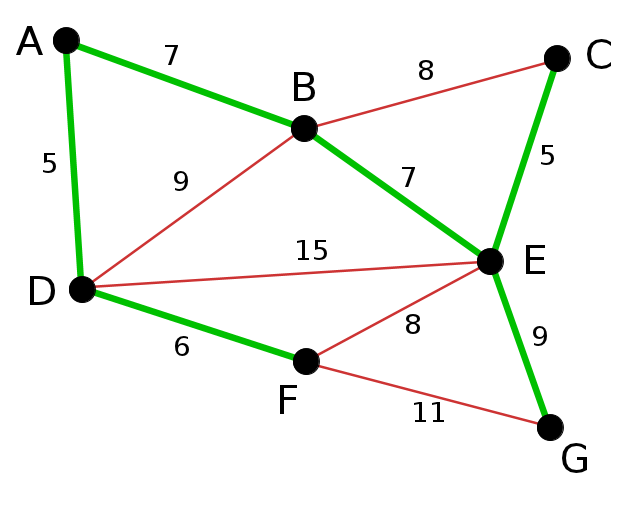
এরপর সবথেকে ছেোট এজ হলো EF, এটাকে আমরা নিতে পারবোনা কারণ EF নিলে একটি সাইকেল তৈরি হয়ে যাবে,E থেকে F তে যাবার রাস্তা আগে থেকেই আছে,তাই এজটি নেয়ার কোনো দরকার নেই। এভাবে BC,DB সহ লাল রঙের এজগুলো বাদ পড়বে কারণ এরা সাইকেল তৈরি করে।

সবশেষে EG যোগ করলে আমরা mst পেয়ে যাবো।

এখন আমরা ইম্প্লিমেনটেশনে আসি। আমাদের প্রথম কাজ হলো সর্ট করা। পরের কাজ হলো একটি একটি এজ নিয়ে চেক করা যে দু প্রান্তের নোড দুটির মধ্য পথ আছে নাকি,অর্থাত তারা একই কম্পোনেন্টের ভিতর আছে নাকি। এটা চেক করতে লাগবে ডিসজয়েন্ট সেট। ডিসজয়েন্ট সেট নিয়ে টিউটোরিয়ালে দেখিয়েছিলাম কিভাবে দুটি নোড একই সাবগ্রাফে আছে নাকি বের করতে হয়। তুমি সেই কাজটিই এখানে করবে। তারপর একই সাবগ্রাফে না থাকলে আগের মত Union ফাংশন কল দিয়ে তাদের একসাথে নিয়ে আসবে আর এজটি একটি ভেক্টর বা অ্যারেতে সেভ করে রাখবে।

নিচে একটা ইমপ্লিমেন্টেশন দিলাম, আশা করি এটা কপি না করে নিজে বুঝে লিখবে:

কমপ্লেক্সিটি অ্যানালাইসিস:
মনে করি $E$ হলো এজ সংখ্যা। এজগুলোকে সর্ট করতে হবে, সেটার কমপ্লেক্সিটি $O(ElogE)$, এরপরে শুধু এজগুলোর উপর লিনিয়ার লুপ চালাতে হবে। তাহলে মোট কমপ্লেক্সিটি $O(ElogE)$।

mst সম্পর্কিত অনেকগুলো সহজ প্রবলেম দিয়েছি প্রিমস এর টিউটোরিয়ালে,ওগুলো সলভ করে প্র্যাকটিস করতে পারো। আরেকটু ভালো প্রবলেম করতে চাইলে দেখো:

২য় সেরা স্প্যানিং ট্রি?
অনেক সময় প্রবলেমে বলা হয় সেকেন্ড বেস্ট MST বের করতে। এটা আমরা ব্রুট ফোর্স দিয়ে বের করতে পারি। MST বের করা পর যে এজগুলো পাবো সেগুলার প্রত্যেকটা একবার করে বাদ দিয়ে নতুন করে MST বের করতে হবে, এভাবে করে যে MST টা মিনিমাম হবে সেটাই সেকেন্ড বেস্ট MST।

http://uva.onlinejudge.org/external/103/10369.html
http://uva.onlinejudge.org/external/117/11733.html