ব্যাকট্র্যাকিং একধরণের ব্রুটফোর্স টেকনিক। ব্রুটফোর্সের মতই এটা সম্ভাব্য সবধরণের বিন্যাস-সমাবেশ থেকে ফলাফল খুজে নিয়ে আসে। যেমন ধর তোমাকে ঢাকা থেকে চট্টগ্রামে যাবার সবথেকে ছোটো পথ খুজে বের করতে বলা হলো। তুমি ডায়াক্সট্রার দেয়া অ্যালগোরিদম ব্যবহার না করে যাবার যত পথ আছে সবগুলো খুজে বের করলে এবং তারপর তারমধ্যে থেকে সবথেকে ছোট কোনটা সেটা বের করলে, এটা হলো ব্রুটফোর্স বা কমপ্লিট সার্চ।
এই লেখাটা পড়ার আগে অবশ্যই রিকার্সন সম্পর্কে ভালো ধারণা থাকতে হবে।
সার্চস্পেসের আকার ছোটো হলে এটা খুবই কার্যকর একটা পদ্ধতি। সার্চস্পেস হলো কতটুকু অংশজুড়ে তোমার সলিউশন থাকতে পারে সেইটুকু। যেমন তোমাকে যদি ১০সাইজের দুটি সেট দিয়ে বের করতে বলে ২য় সেট ১মটির সাবসেট কিনা তাহলে খুব সহজে তুমি ব্যাকট্র্যাক করে $2^{10}=1024$ টি সেট বের করে সবগুলোর সাথে মিলিয়ে দেখতে পারো, কিন্তু সেটের আকার ১০০ হলে তোমার এভাবে সলিউশন বের করার জন্য এই জীবনকাল যথেষ্ট নয়!
যেসব প্রবলেমের পলিনমিয়াল কোনো সলিউশন আমরা এখনো জানিনা অর্থাৎ NP বা NP-hard ক্যাটাগরির প্রবলেম সেগুলোকে ব্যাকট্র্যাক করেই সমাধান করতে হয়। ব্যাকট্র্যাকিং কোড লেখার আগে কমপ্লেক্সিটির ব্যাপারে খুব সতর্ক থাকতে হবে।
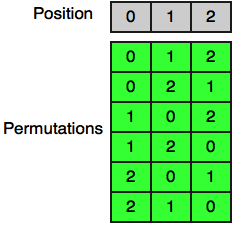
এখন আমরা দেখবো কিভাবে ব্যাকট্র্যাক করে $0$ থেকে $n-1$ পর্যন্ত সংখ্যাগুলোর প্রতিটি পারমুটেশন বের করা যায়। যদি $n=2$ হয় তাহলে পারমুটেশনগুলো হবে:
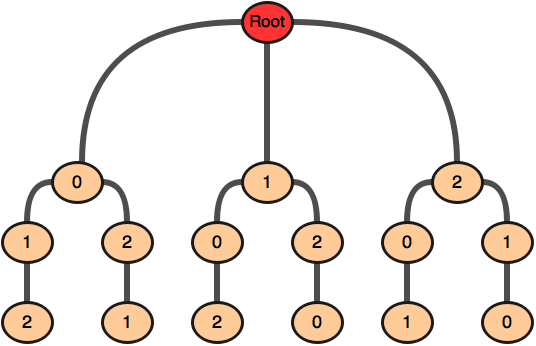
সহজে বোঝার জন্য আমরা পারমুটেশনগুলোকে একটা ট্রি আকারে দেখি:
এই ট্রি তে রুট থেকে যেকোনো পথে আগাতে থাকলে একটা করে পারমুটেশন পাওয়া যাবে। আমরা একটা রিকার্সিভ ফাংশন লিখবো যেটা এই ট্রি এর সবগুলো পথে একবার করে ঘুরে আসবে। আমাদেরকে সত্যি সত্যি অ্যাডজেসেন্সি ম্যাট্রিক্স দিয়ে ট্রি বানিয়ে ফেলা দরকার নেই, ছবিটা দেয়া হয়েছে সহজে বোঝার জন্য।
মনে করো আমাদের ফাংশনের নাম হলো $generate(idx)$। $idx$ মানে হলো এখন আমরা $idx$ তম পজিশনে একটা সংখ্যা বসাতে চাই। নিচের সুডোকোডটি দেখো, এরপর আমি ব্যাখ্যা করছি:
|
1 2 3 4 5 6 7 8 9 10 |
procedure generate(idx) if idx == n print position return for i from 0 to n if taken[i] = False taken[i] <- true position[idx] = i generate(idx+1) taken[i] <- false |
৫ নম্বর লাইনে আমি $0$ থেকে $n$ পর্যন্ত একটি লুপ চালিয়েছি। ৬ নম্বর লাইনে দেখছি যে $i$ সংখ্যাটি এরই মধ্যে নেয়া হয়েছে নাকি। যদি না নেয়া হয়ে থাকে তাহলে $idx$ তম পজিশনে $i$ বসিয়ে রিকার্সিভলি $idx+1$ বাকি পজিশনগুলোর জন্য প্রবলেমটা সলভ করছি।
ইন্টারেস্টিং ব্যাপার হলো রিকার্সিভলি $generate(idx+1)$ এর জন্য সলভ করার পর আমরা taken[i] <- false করে দিচ্ছি। কারণ $i$ তম সংখ্যাটা $idx$ পজিশনে বসানোর পর আবার সেই পজিশন থেকে $i$ কে ফেলে দিয়ে $i+1$ কে একই পজিশনে বসিয়ে রিকার্সিভলি সলভ করবো।
ব্যাকট্র্যাকিং করার জেনারেল আইডিয়াটা হলো:
১. প্রতিটি ফাংশন কলে সম্ভাব্য অপশনগুলোর একটি বাছাই করো।
২. বাকি অপশনগুলো থেকে রিকার্সিভলি সমাধান বের করার চেষ্টা করো।
৩. বাছাই করা অপশনটি ফেলে দিয়ে অন্য আরেকটি নিয়ে আবার চেষ্টা করো।
এখন তোমার কাজ হবে সুডোকোডটাকে আসল কোডে রূপান্তর করা। যদি এটা পারো তাহলে তুমি আরো কিছু একইরকম সমস্যা সহজেই সমাধান করতে পারবে। যেমন তোমাকে যদি একটা স্ট্রিং “abcd” দিয়ে বলা হয় সবরকম পারমুটেশন জেনারেট করতে তাহলে একইভাবে সহজেই করতে পারবে। কিন্তু স্ট্রিংটায় যদি এই ক্যারেকটার একাধিকবার থাকে (যেমন “abbcdd”) তাহলে একটু ঝামেলায় পড়বে, দেখবে একই পারমুটেশন বারবার জেনারেট হচ্ছে। এটা এড়াতে তোমাকে একটা ফ্ল্যাগ রেখে একই পজিশনে একই ক্যারেক্টার একাধিকবার বসিয়ে রিকর্সিভলি সলভ করা বন্ধ করতে হবে।
প্র্যাকটিসের জন্য নিচের সমস্যাগুলো সমাধান করো:
Determine The combination
Prime Ring problem
House of santa clause
All Walks of length n
Following orders
আপাতত এখানেই শেষ, পরের পর্বে ব্যাকট্র্যাকিং দিয়ে সমাধান করা যায় এমন কিছু সমস্যা দেখবো।
ফেসবুকে মন্তব্য
Powered by Facebook Comments


UVA 524 এ WA দিচ্ছে… কোন special কিছু জানা আছে তোমার,যার কারণে WA দিতে পারে ?? আমি কোন error বের করতে পারিনি… 🙁
Accepted !!! After 5 WA !!! Frustrated হয়ে পড়ছিলাম !!!
uva 677 এ,
১) একই নোডের মধ্যে কি connection থাকতে পারে ???
২) গ্রাফ কি always connected হবে ?
আচ্ছা ব্রুট-ফোর্স বলতে আসলে কি বোঝায়? সিএস ব্যাকগ্রাউন্ডের অনেকের মুখে শুনেছি, কনটেক্সটা কি একটু বুঝিয়ে বলা যায়?
ব্রটফোর্স হলো সম্ভাব্য যতরকম অপশন আছে সব দেখে সেখান থেকে সঠিক উত্তর খুজে বের করা। লেখার শুরুতেই উদাহরণ দিয়েছি, ঢাকা থেকে চট্রগ্রামে যাবার সবথেকে ছোট পথ খুজে বের করতে যদি আপনি যত পথ আছে সবগুলো দিয়েই একবার করে ঘুরে আসেন তাহলে সেটা হবে ব্রুটফোর্স অ্যালগোরিদম, স্মার্ট কোনো অ্যালগোরিদম ব্যবহার করলে আপনার সবগুলো পথ দিয়ে ঘুরে আসা লাগবেনা। আবার ধরুন আপনার পাসওয়ার্ড হ্যাক করতে যদি আমি ইংরেজীতে যত শব্দ আছে সবগুলো বসিয়ে চেষ্টা করি সেটা হবে ব্রুটফোর্স অ্যাটাক। সোজা কথায় ব্রুটফোর্স হলো গায়ের জোরে কাজ করা।
অনেক ধন্যবাদ এমন ভালো একটা পোস্টের জন্য। কিন্তু আমি কিছুদিন যাবত ভেবে কোন অংশ বদলেও কোনভাবেই রিপিটেটিভ সংখ্যাসহ আরের পারমুটেশন বের করতে পারছিনা ব্যাকট্র্যাকিং দিয়ে(যেমনঃ abbcd), একই পারমুটেশন বার বার রিপিট হচ্ছে। আমি অনেক ভাবেই চেষ্টা করেছি কিন্তু পারছিনা।