তোমাকে একটা আনওয়েটেড গ্রাফ এবং একটা সোর্স নোড দেয়া আছে। তোমাকে সোর্স নোড থেকে সর্বোচ্চ দৈর্ঘ্যের পাথ বের করতে হবে। এটাই হলো লংগেস্ট পাথ প্রবলেম। প্রশ্ন হলো কিভাবে প্রবলেমটা সলভ করবে?
এটা আমার খুবই প্রিয় একটা ইন্টারভিউ প্রশ্ন। এখন পর্যন্ত প্রায় ৭-৮টা ইন্টারভিউতে আমি এই প্রশ্ন করেছি, মাত্র ২জন সহজেই উত্তর দিতে পেরেছে, ১জন হিন্টস দেয়ার পর পেরেছে, বাকিরা সবাই ভুল উত্তর দিয়েছে। অ্যালগোরিদম কোর্সে এ+ অনেকেই পায়, কিন্তু এধরণের প্রশ্ন করলে বোঝা যায় ক্যান্ডিডেট আসলে কতখানি জানে।
প্রশ্নটা করার পর সবাই প্রথমে যে ভুল করে সেটা হলো জিজ্ঞেস করে না সর্বোচ্চ দৈর্ঘ্যের পাথের সংজ্ঞা কি, আমি চাইলে দুটি নোডের মধ্যে অসীম সংখ্যকবার আসা-যাওয়া করে দৈর্ঘ্য অসীম করে ফেলতে পারি। তাই লংগেস্ট পাথের আরো ভালো কোনো সংজ্ঞা দরকার সমাধান করা জন্য। ধরা যাক আমি এমন একটা লংগেস্ট পাথ চাই যেখানে কোনো নোডে একবারের বেশি যাওয়া যাবে না। এখন আর দৈর্ঘ্য অসীম হবার কোনো সুযোগ নেই।
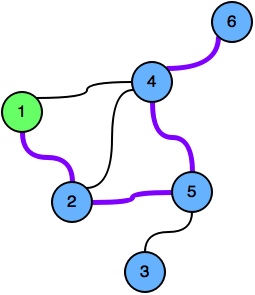
ছবিতে ১ নম্বর নোড থেকে সর্বোচ্চ দৈর্ঘ্যের পাথ দেখানো হয়েছে যার দৈর্ঘ্য হলো ৪ (১->২->৫->৪->৬)।
সমাধান নিয়ে চিন্তা করার আগে পরের প্রশ্ন হলো গ্রাফটা কি ডিরেক্টেড নাকি আনডিরেক্টেড। ধরে নাও গ্রাফটা আনডিরেক্টেড এবং সর্বোচ্চ ১০০,০০০ টা নোড থাকতে পারে।
এই প্রবলেমের অনেক ধরণের ভূল সমাধান দিতে দেখেছি ক্যান্ডিডেটদের, যেমন:
- কেও কেও গ্রাফের এজগুলোর ওয়েট -১ ধরে শর্টেস্ট পাথ বের করার চেষ্টা করে। এটা কোনোভাবেই কাজ করবে না, ইনফিনিটি লুপে আটকে যাবে।
- কেও কেও ডায়নামিক প্রোগ্রামিং ব্যবহার করে সমাধান করতে চেষ্টা করে, এটাও কাজ করবে না এবং লুপে আটকে যাবে।
- ম্যাক্স ফ্লো ব্যবহার করতে চায় অনেকে কিন্তু সেটাও কাজ করবে না।
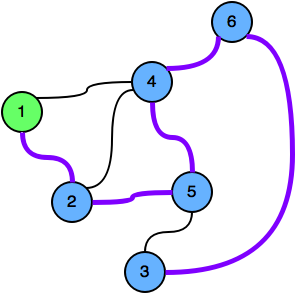
তাহলে সমাধান টা কি? মনে করি গ্রাফটার নোড সংখ্যা $n$। যেহেতু $n$ এর মান অনেক বড় হতে পারে, তাই অবশ্য পলিনোমিয়াল সলিউশন দরকার। এখন এমন একটা গ্রাফের কথা চিন্তা করো যেটায় সোর্স থেকে লংগেস্ট পাথের দৈর্ঘ্য হলো $n-1$। যেমন নিচের গ্রাফটা:
এই গ্রাফটিতে লংগেস্ট পাথের দৈর্ঘ্য হলো $n-1$ যেখানে $n=6$। তারমানে হলো গ্রাফটাতে এমন একটা সোর্স নোড আছে যেখান থেকে যাত্রা শুরু করে সবগুলো নোড একবার করে ভ্রমণ করা যায় কোনো নোড পুনরাবৃত্তি না করেই। এ ধরণের পাথকে বলা হয় হ্যামিল্টন পাথ! তুমি যদি গ্রাফথিওরি নিয়ে কিছুটা পড়ালেখা করে থাকো তাহলে অবশ্য জানার কথা যে হ্যামিল্টন পাথ প্রবলেম একটা এন-পি কমপ্লিট (NP-complete) প্রবলেম। এন-পি কমপ্লিট কোনো প্রবলেমকে পলিনমিয়াল সময়ে সমাধান করার কোনো উপায় এখন পর্যন্ত কারো জানা নেই।
দেখতেই পাচ্ছো হ্যামিল্টন পাথ প্রবলেমকে খুব সহজেই লংগেস্ট পাথ প্রবলেমে কনভার্ট করা যায়। একটা গ্রাফে কোনো সোর্স থেকে এমন একটা লংগেস্ট পাথ বের করতে হবে যেন পাথের দৈর্ঘ্য হয় $n-1$, এটাই হ্যামিল্টন পাথ প্রবলেম। লংগেস্ট পাথ প্রবলেমকে পলিনমিয়াল সময়ে সমাধান করা গেলে হ্যামিল্টন পাথ প্রবলেমও সমাধান হয়ে যেত!
তাহলে দেখতেই পাচ্ছি যে লংগেস্ট পাথ প্রবলেমের কোনো পলিনমিয়াল সলিউশন নেই। নোড সংখ্যা যদি খুব অল্প হয় তাহলে ব্যাকট্র্যাকিং করে এই সমস্যা সমাধান করা সম্ভব, কিন্তু এটার কমপ্লেক্সিটি এক্সপোনেনশিয়াল(exponential)। লংগেস্ট পাথ হলো একটা এন-পি হার্ড প্রবলেম।
এখন প্রশ্ন হলো কেন হ্যামিল্টন পাথ প্রবলেম এন-পি কমপ্লিট কিন্তু লংগেস্ট পাথ এন-পি হার্ড? যদি এটার উত্তর না জেনে থাকো তাহলে আমার এই লেখাটা পড়ে ফেলো।
হ্যাপি কোডিং
ফেসবুকে মন্তব্য
Powered by Facebook Comments

ভাইয়া, জনসন’স অ্যালগরিদম নিয়ে কিছু পোস্ট দিয়েন।