আগের পর্বে আমরা ফিবোনাচ্চি নাম্বার নিয়ে আলোচনা করেছি। আমরা দেখেছি কিভাবে ডাইনামিক প্রোগ্রামিং ব্যবহার করে রিকার্সিভলি এবং ইটারেটিভলি ফিবোনাচ্চি সংখ্যা জেনারেট করা যায়। এই পর্বে আমরা কথা বলবো শর্টেস্ট পাথ প্রবলেম নিয়ে এবং সেটা নিয়ে আলোচনা করার সময় ডিপির কিছু নতুন প্রোপার্টি নিয়ে জানবো।
যদিও শর্টেস্ট পাথ গ্রাফ থিওরির একটা প্রবলেম, এই লেখা বুঝতে গ্রাফ নিয়ে না জানলেও চলবে।
মনে করো আমাদেরকে এক শহর থেকে অন্য শহরে যাবার শর্টেস্ট পাথ খুজে বের করতে হবে। শহর আছে মোট $n$ টি। $0$ হলো প্রথম শহর, এবং $n – 1$ হলো শেষ শহর। কোন শহর থেকে কোন শহরে সরাসরি যাওয়া যায় এবং শহরগুলোর মধ্যে দুরত্ব কত সেটা অ্যারো দিয়ে দেখিয়ে দেয়া আছে নিচের ছবির মতো:
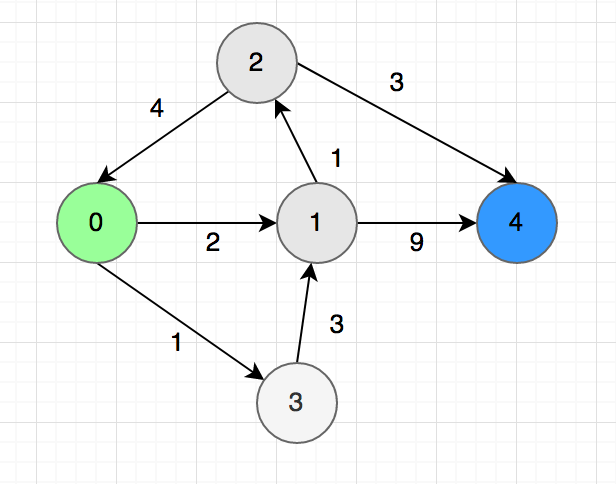 এখন আমাদের প্রবলেমটা হলো $0$ থেকে $n-1$ এ যাবার শর্টেস্ট পাথের দৈর্ঘ্য কত? এখন আমরা কয়েকটা ধাপে সমস্যাটা ফর্মুলেট করবো।
এখন আমাদের প্রবলেমটা হলো $0$ থেকে $n-1$ এ যাবার শর্টেস্ট পাথের দৈর্ঘ্য কত? এখন আমরা কয়েকটা ধাপে সমস্যাটা ফর্মুলেট করবো।
প্রবলেমের প্যারামিটার বা স্টেট নির্ধারণ:
প্রথমেই আমাদের বের করতে হবে প্রবলেমটাকে কি কি প্যারামিটার বা স্টেট দিয়ে প্রকাশ করা যায়। স্টেট শব্দটা মাথায় রেখো, সামনে অনেক বার এটা ব্যবহার হবে। আমাদের স্টেট হবে এক্ষেত্রে তুমি বর্তমানে কোন শহরে আছো সেটা। ধরে নিলাম তুমি বর্তমানে $u$ তম শহরে আছো এবং আমাদের প্রবলেমটাকে আমরা $f(u)$ ফাংশন দিয়ে প্রকাশ করবো। ফিবোনাচ্চির মতো আমাদেরকে এখন একটা রিকার্সিভ রিলেশন বের করতে হবে।
স্টেট ট্রানজিশন এবং রিকার্শন:
আমরা জানিনা শহর $u$ থেকে কোন শহরে গেল দ্রুততম উপায়ে গন্তব্য পৌছাতে পারবো। এই ধাপে এসে আমরা সেটা অনুমান করবো। প্রতিটা অনুমান হবে একটা করে সাব-প্রবলেম। ছবিতে শহর $0$ থেকে $1$ এবং $3$ এ যাওয়া যায়। তাহলে $f(0)$ থেকে আমরা নিচের শর্টেস্ট পাথ পাবো এই ফর্মূলা দিয়ে:
$f(0) = min(f(1) + 2, f(3) + 1)$
আইডিয়াটা হলো প্রতিটা শহর থেকে আমরা অন্য সব শহরে যাবো এবং সেখান থেকে শর্টেস্ট পাথ খুজে বের করার চেষ্টা করবো। সবগুলো অনুমানের মধ্যে যেটা সবথেকে ছোট সেটাই হবে উত্তর। জেনারেলাইজড করে লিখলে:
$f(n – 1) = 0 \\f(u) = min(f(u, v) + w(u, v)) \ where \ (u,v) \in E \ for\ u \ne n – 1$
এখানে $w(u, v)$ হলে $u$ থেকে $v$ তে যাবার দূরত্ব।
সাবপ্রবলেম/স্টেট অর্ডারিং:
এখন একটু চিন্তা করো এই রিকার্শন চালিয়ে দিলে কিভাবে ফাংশন কল হবে।
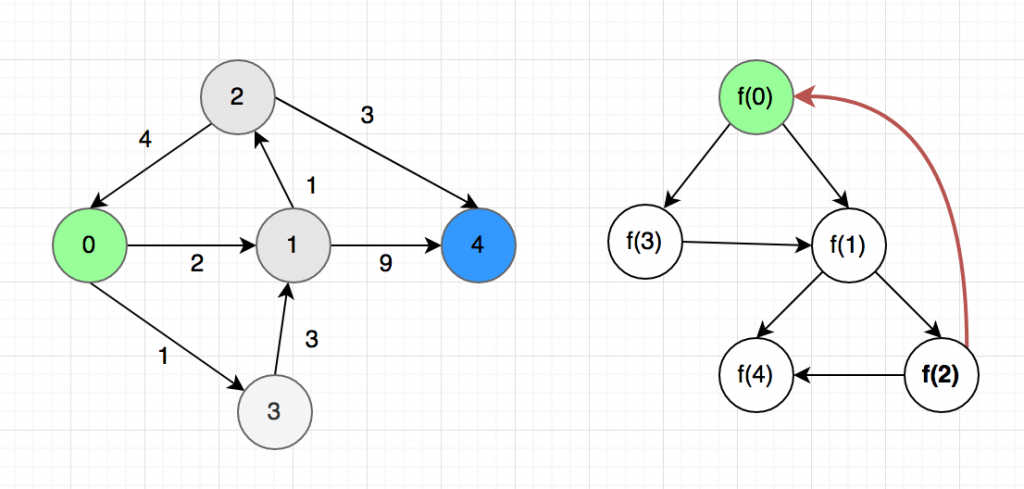 এবার আমরা একটু সমস্যা পড়ে গিয়েছি, সাবপ্রবলেমগুলোর মধ্যে সাইকেল তৈরি হয়ে গিয়েছে। $f(0)$ এর মান জানতে $f(2)$ জানতে হবে কিন্তু $f(2)$ আবার $f(0)$ এর উপর নির্ভরশীল। এই সলিউশন ইমপ্লিমেন্ট করলে আমাদের কোড ইনফাইনাইট লুপে আটকে যাবে।
এবার আমরা একটু সমস্যা পড়ে গিয়েছি, সাবপ্রবলেমগুলোর মধ্যে সাইকেল তৈরি হয়ে গিয়েছে। $f(0)$ এর মান জানতে $f(2)$ জানতে হবে কিন্তু $f(2)$ আবার $f(0)$ এর উপর নির্ভরশীল। এই সলিউশন ইমপ্লিমেন্ট করলে আমাদের কোড ইনফাইনাইট লুপে আটকে যাবে।
এত কষ্ট করে একটা ভুল সমাধান বের করার উদ্দেশ্য আসলে তোমাদের DAG বা ডিরেক্টেড অ্যাসাইক্লিক গ্রাফ কনসেপ্টটার সাথে পরিচয় করিয়ে দেয়া। DAG মানে হলো একটা ডিরেক্টেড গ্রাফ যেখানে কোনো সাইকেল নেই। ডাইনামিক প্রোগ্রামিং সলিউশন কাজ করবে শুধুমাত্র তখনই যখন সাবপ্রবলেমগুলো একটা DAG তৈরি করবে। সাইকেল থাকলেই সাবপ্রবলেমগুলা ইনফিনিট লুপে আটকে যাবে।
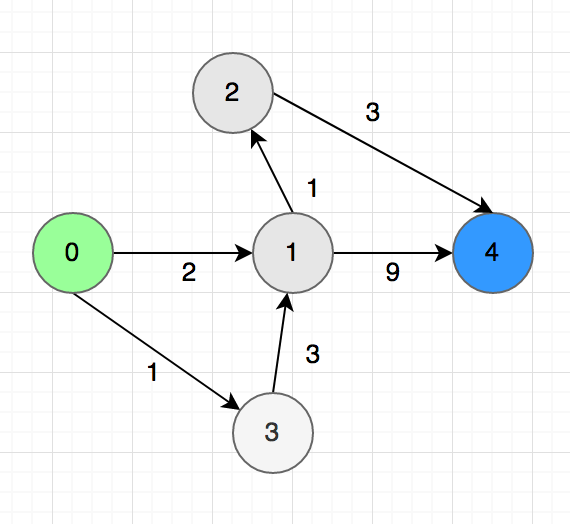
DAG এ শর্টেস্ট পাথ প্রবলেম আমাদের বের করা ফর্মূলা দিয়েই সমাধান করা যাবে। উপরের গ্রাফে 2->0 অ্যারোটা মুছে দিলেই গ্রাফটা অ্যাসাইক্লিক হয়ে যাবে।
অ্যাসাইক্লিক গ্রাফের জন্য কোডটা হবে এরকম:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
#define MAX_N 20 #define INF 99999999 #define EMPTY_VALUE -1 int w[MAX_N][MAX_N]; int mem[MAX_N]; int f(int u, int n) { if (u == n - 1) { return 0; } if (mem[u] != EMPTY_VALUE) { return mem[u]; } int ans = INF; for (int v = 0;v < n;v++) { if (w[u][v] != INF) { ans = min(ans, f(v, n) + w[u][v]); } } mem[u] = ans; return mem[u]; } |
ইন্টারেস্টিং ব্যপার হলো সাইক্লিক গ্রাফেও ডিপি দিয়ে শর্টেস্ট পাথ বের করা যায় তবে সেক্ষেত্রে একটা অতিরিক্ত প্যারামিটার k যোগ করতে হয় যেটা দিয়ে বুঝায় ‘সর্বোচ্চ $k$ টা এজ ব্যবহার করে শর্টেস্ট পাথ কত?’। তখন সেটাই হয়ে যাবে বেলম্যানফোর্ড অ্যালগরিদম!
কমপ্লেক্সিটি:
কোডে আমরা দুটো প্যারামিটার $u$ আর $n$ পাস করলেও প্রবলেমের স্টেট আসলে শুধু প্রথম প্যারামিটারটাই। $u$ এর ভ্যালু হতে পারে $0$ থেকে $n-1$ পর্যন্ত। প্রতিটা সাবপ্রবলেমের জন্য আবার সেই শহরের সাথে কোন শহরের কানেকশন আছে সেটা আমাদের চেক করতে হচ্ছে একটা লুপ চালিয়ে, কানেকশন থাকতে পারে সর্বোচ্চ $n$ টা। মোট কমপ্লেক্সিটি পেতে আমারা স্টেট সংখ্যা এবং ভিতরের কমপ্লেক্সিটি গুণ করে দিয়ে যাবো $O(n * n)$।
ইটারেটিভ ভার্সন:
এই প্রবলেমের ইটারেটিভ ভার্সন লেখা একটু কঠিন তবে সম্ভব। আমরা জানি ইটারেটিভ ডিপির জন্য সাবপ্রবলেমগুলোকে টপোলজিকাল অর্ডারে সাজিয়ে নিতে হবে। কারণ প্রতিটা স্টেটে তোমাকে নিশ্চিত করতে হবে যে তুমি ডিপেন্ডেন্ট স্টেটগুলো আগেই ক্যালকুলেট করে এসেছো। ফিবোনাচ্চির জন্য কাজটা খুব সহজ ছিল, $0,1,2,3…$ এভাবে স্টেটগুলো আগাচ্ছিলো, কিন্তু গ্রাফের জন্য ব্যাপারটা একটু কঠিন। গ্রাফে নোডগুলোকে কিভাবে টপোলজিকাল সর্টিং করতে হয় সেটা তুমি এখান থেকে শিখে নিতে পারো। উপরের উদাহরণে সর্ট করার পর আমরা পাবো ${0, 3, 1, 2, 4}$। এখান এই অ্যারের উল্টা দিক থেকে লুপ চালালে তুমি ডিপির টেবিল বিল্ডআপ করতে হবে।
এই প্রবলেমের ইটারেটিভ সলিউশন তুমি আপাতত না লিখতে পারলেও সমস্যা নেই, ইটারেটিভ সলিউশনটা জটিল এবং তেমন কোনো অ্যাডভান্টেজ দিবে না। ইটারেটিভ ডিপি আমরা আরো ভালো লেখা শিখবো যখন LIS, ন্যাপস্যাক সলভ করবো।
এখন পর্যন্ত তাহলে তুমি শিখলে:
- সাবপ্রবলেমের প্যারামিটার বা স্টেট কিভাবে নির্ধারণ করা যায়
- কিভাবে এক স্টেট থেকে অন্য সব স্টেটে গিয়ে অপটিমাল সলিউশন বের করে আনা যায়
- DAG কাকে বলে, সাইক্লিক ডিপেন্ডেসি থাকলে ডিপি দিয়ে প্রবলেম সলভ করা যায় না।
ডিপি সলভ করতে এখনো কনফিডেন্স পাচ্ছো না? সমস্যা নাই, এটা কেবলই শুরু, পরের পর্ব পড়ার পর তুমি নিজেই দুয়েকটা প্রবলেম সলভ করার কনফিডেন্স পাবে।
ফেসবুকে মন্তব্য
Powered by Facebook Comments

আবারো DP নিয়ে আসাধারণ একটি পোস্ট।
দারুন হইছে…….:)
ডিপি … সুন্দর ।
UVA 10130 supersale problem acceptd হয়েছে… runtime 0.792s 🙂
aro fast accepted hobea jodi apni memozition pordhoti na korea bottom-up solution vabea solve koren… 🙂
Getting Time Limit.
Problem: Uva 10130.
My code:http://ideone.com/iTuikC
cin বাদ দিয়ে scanf নাও। তবে আসল সমস্যা হলো dp অ্যারেটা মেমসেট করতে অনেক সময় লাগছে, 1000*50 ডাইমেনশন নাও, AC হবে। ডিপি প্রবলেমে সবসময় এই ব্যাপারটা খেয়াল রাখতে হবে, যত বেশি মেমরি নেয়া হবে সেটা মেমসেট করতে তত বেশি সময় লাগবে।
ভাই uva 10819 – Trouble of 13-Dots এই সমস্যাটা কিভাবে সমা্ঢান করব
ভাইয়া, আমার কোড আমার pc তে ঠিকমতো কাজ করছে। কিন্তু UVA তে wrong answer দেখাচ্ছে। critical input গুলো কী বলা যাবে? আর আমার কোডটা একটু চেক দেখবেন প্লিজ। http://ideone.com/HaQsCu
ভাইয়া ডিপি এর শুরুটা ভালই হোলো । NCR এর প্রব্লেম টা সলভ করলাম ।
ভাইয়া ফাহিম ভাইয়ের ব্লগ থেকে জোবায়ের ভাই এর ব্লগ এর লিঙ্ক টা পাই । লিঙ্ক ঃ
http://zobayer.blogspot.com/2009/12/cse-102-attacking-recursion.html
ভাইয়া এখান থেকে একটা নতুন তথ্য পেয়েছি । সেটা হোলো প্রায় যেকোনো লুপিং এর কোড নাকি রিকার্শন এর মাধ্যমে করা যায় । ওখানে আপনার একটা কমেন্ট ও দেখেছিলাম । মানে আপনিও ব্লগটি পরেছেন ।
এখন সমস্যা টা হোলো Incremental for লুপ টা রিকার্শনের মাধ্যমে ভালোভাবেই বুঝতে পেরেছি । কিন্তু Decremental for লুপ টা তে একটু সমস্যা হচ্ছে । যদিও চিত্র টা দেখে কিছুটা বুঝেছি তারপরো খটকা রয়ে গেছে ।
=> একই রকম রিকার্শন এর কোড কিন্তু কাজ করবে দুটো দু রকম । এ জায়গাটায় একটু প্রব্লেম আছে । এটা কি একটু ক্লিয়ার করে দেয়া যায় ??
ধন্যবাদ ।
vaia, The hyperlink of ‘Greedy’ approach is not working.
vi input e “২. কোরম্যানের-বই ভর: ৭ইউনিট,৪০০টাকা” eta koi???
I believe there is a mistake in the recursive function in the section “State Transition and Recursion”. The recursive call will be f(v) instead of f(u,v)